Practice Test: Elementary Mathematics (68)
Answer Key, Sample Responses, Evaluation Chart, and Score Calculation Tool
Answer Key
Fill in your answers below and then print this answer key to save your work. Alternatively, you can print the answer key first to fill it out offline as you take the practice test. Note that the correct responses will be displayed on the printed answer key, so you may want to cover them until you have completed the practice test and are ready to check your answers.
When you have finished the practice test, click on "show answers" to see how well you did on each objective. In addition, use the Evaluation Chart to determine how many questions within each objective you answered correctly.
You will not receive a score for the practice test, and there is no passing score for the practice test. However, to get a sense of how well you did, use the Score Calculation Tool to better gauge your performance and degree of readiness to take an MTEL test at an operational administration.
NOTE: When you take the actual test, you will receive a score report that provides subarea-level performance, not objective-level performance. Information about test results can be found at Score Report Explanation.
| Question Number | Your Response | Correct Response |
Related Objectives and Rationale |
||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A |
Objective 001 Correct Response: A. Base 3 uses the digits 0, 1, and 2 and has place value positions defined by powers of 3. The rightmost placeholder position represents 3 to the zero power the position to the left is 3 to the first power the position to the left of that is 3 squared and so on.
The number 1 0 1 0 1 in base 3 can be written in expanded form as shown: Incorrect Response: B. This response may be the result of misinterpreting 3 to the zero power to be equal to 3 in the expression 81 + 9 + 1 times 3 to the zero power ). Incorrect Response: C. This response may be the result of misinterpreting the rightmost place value position as 3 to the first power and also misinterpreting the value of 1 times 3 to the first power to be 1, which would result in a computation of 1 times 3 to the fifth power plus 1 times 3 cubed plus 1 times 3 to the first power = 243 + 27 + 1 = 271. Incorrect Response: D.This response may be the result of misinterpreting the rightmost place value position as 3 to the first power which would result in a computation of 1 times 3 to the fifth power plus 1 times 3 cubed plus 1 times 3 to the first power = 243 + 27 + 3 = 273. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | A |
Objective 001 Correct Response: A. The absolute value of a number represents its magnitude, or its distance from 0. When comparing negative numbers, the number with the least absolute value is closest to 0 and greatest in value. Of the numbers given, negative 2.1 has the least absolute value: Absolute value of negative 2.1 = 2.1. Incorrect Response: B. Absolute value of negative 2.4 = 2.4, which is greater than Absolute value of negative 2.1 = 2.1. This means that negative 2.4 is located farther to the left on a number line than negative 2.1, which means negative 2.4 is less than negative 2.1. Incorrect Response: C. This response is equivalent to negative 2.2, which has a greater absolute value than negative 2.1. This implies that negative 2.2 is less than negative 2.1. Incorrect Response: D. This response is equivalent to negative 2.8, which has the greatest absolute value of all numbers in the set. Since the number is negative, this means that negative 2.8 is the farthest to the left of zero on a number line of all numbers in the responses, which means it has the least value. |
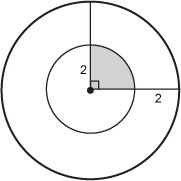
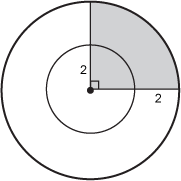
|||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | D |
Objective 001 Correct Response: D. The side lengths of the cube are all equal, and the volume of the cube is the product of its side lengths. The equation V = s cubed relates the volume of the cube, V, to the length of a side, s. The inverse of this equation—the equation that describes how to determine s when V is known—can be found by taking the cube root of both sides of the equation: Incorrect Response: A. This statement is true, but it does not lead to a direct comparison of how finding an edge length of a cube from its volume is related to finding a volume of a cube from its edge length. Incorrect Response: B. This statement is true, but the edge length of a cube and its volume are related by iterative multiplication (i.e., exponentiation). This statement lacks the depth of the detail that is captured in the correct response. Incorrect Response: C. This statement is true but does not lead to a direct comparison of how finding an edge length of a cube from its volume is related to finding a volume of a cube from its edge length. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | B |
Objective 001 Correct Response: B. The 35 chairs may be arranged into 5 rows, with 7 chairs per row. This arrangement fulfills the criteria provided. Incorrect Response: A. There are multiple ways to arrange 30 chairs such that all the provided criteria are met. For example, the chairs could be arranged into 2 rows, with 15 chairs per row, or 3 rows, with 10 chairs per row. Incorrect Response: C. There are multiple ways to arrange 36 chairs such that all the provided criteria are met. For example, the chairs could be arranged into 2 rows, with 18 chairs per row, or 3 rows, with 12 chairs per row. Incorrect Response: D. Prime numbers such as 37 can only be factored into a product of 1 and the number itself. In the context of this problem, there is only one way that 37 chairs can be arranged with an equal number of chairs per row, and that is 1 row of 37 chairs. This means that the last criterion cannot be met. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | D |
Objective 001 Correct Response: D. radical 12 is an irrational number since it cannot be written as a fraction in the form P divided by q where p and q are integers. The value of radical 12 is between 3 and 4 since Radical 9 is less than radical 12 is less than radical 16, which implies 3 is less than radical 12 is less than 4. This means that radical 12 could represent point X on the number line shown. Incorrect Response: A. A rational number can be written as a fraction in the form , P divided by q where p and q are integers. Since 38 elevenths meets these criteria, it is a rational number. Incorrect Response: B. Radical 7 is an irrational number since it cannot be written as a fraction in the form , P divided by q where p and q are integers. However, the value of Radical 7 is between 2 and 3 since Radical 4 is less than radical 7 is less than radical 9, which implies 2 is less than radical 7 is less than 3. For this reason, Radical 7 cannot represent point X on the number line shown. Incorrect Response: C. A rational number can be written as a fraction in the form , P divided by q where p and q are integers. Since 3.46 = 3 and 46 hundredths which equals 346 over 100 this response is a rational number. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | D |
Objective 001 Correct Response: D. The area of the large rectangle can be obtained from its dimensions or by adding together the areas of the two smaller rectangles that compose it. The dimensions of the large rectangle are 5 times 14, where the 14 represents the sum of the 8 and the 6, and its area is 70. The area of the 5 times 8 rectangle is 40 and the area of the 5 times 6 rectangle is 30. Together, these add to 70. This model is a useful representation for the distributive property of multiplication because it illustrates why the operation of multiplication distributes over addition. That is, it explains why . 5 times the quantity 8 plus 6 equals 5 times 8 plus 5 times 6 Incorrect Response: A. Student B is also correct since 5 times 8 + 5 times 6 = 5 times 14. Incorrect Response: B. Student A is also correct since 5 times 8 + 5 times 6 = 5 times 14. Incorrect Response: C. A repeated addition interpretation of multiplication should refer to a repeated quantity, a number of repetitions, and an overall result. None of these quantities are mentioned here. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | B |
Objective 001 Correct Response: B. The sum of a number and its additive inverse is 0. This equation shows that 3 and negative 3 are additive inverses because their values add to 0. Incorrect Response: A. This equation is a result of the identity property of addition, where the 4 plus 0 returns a value of 4. The identity property of addition can also be used in conjunction with the property of an additive inverse to write 4 minus 0 is equal to 4 plus negative 0 = 4, but this is not the best equation to use to illustrate the concept of an additive inverse. Incorrect Response: C. This equation illustrates the commutative property of addition using integers, but it does not illustrate the concept of an additive inverse. Incorrect Response: D. This equation illustrates the commutative property of addition using a whole number and its reciprocal, but it does not illustrate the concept of an additive inverse. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | C |
Objective 001 Correct Response: C. One-to-one correspondence is a mathematical concept found in counting and, more broadly, in set theory. It is based upon a relationship where each element from one set (e.g., names of numbers, numerals, a collection of textbooks) is uniquely matched to an element from another set (e.g., objects being counted, sections of a spinner, a collection of crayons). This idea is clearly illustrated in this response, since each book is associated with exactly one crayon. Incorrect Response: A. This response associates one object (the textbook) with multiple other objects (crayons), so it does not illustrate the concept of one-to-one correspondence. The relationship shown here is similar to using the number 1 to count each object in a set of 3 objects. Incorrect Response: B. This response associates multiple objects (books) with exactly one object (the crayon), so it does not illustrate the concept of one-to-one correspondence. The relationship shown here is similar to using the numbers 1, 2, and 3 to count a single object. Incorrect Response: D. This response illustrates a complex relationship between two sets that does not follow the definition of a one-to-one correspondence. For example, following the arrows between the sets, the top left text book is associated with the right crayon and, through its subsequent associations, to every other object in both sets. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | C |
Objective 001 Correct Response: C. The correct response is the result of dividing the following expressions as shown: 3.6 times 10 to the seventh power divided by 2.4 times 10 to the fifth power equals 3.6 divided by 2.4 times 10 to the seventh power divided by 10 to the fifth power, which equals 1.5 times 10 squared, which equals 1.5 times 100, which equals 150 Incorrect Response: A. This response may be the result of dividing the rational numbers 3.6 and 2.4 to get a quotient of 1.5, which is correct, but then multiplying that result by 10. This may be due to an error in dividing 10 to the seventh power by 10 to the fifth power or a misconception about how to manipulate the decimal point. Incorrect Response: B. This response may be the result of a misconception about how to apply exponent rules to evaluate the expression . 10 to the seventh power divided by 10 to the fifth power Incorrect Response: D. This response may be the result of a misconception about how to apply exponent rules to evaluate the expression . 10 to the seventh power divided by 10 to the fifth power |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | D |
Objective 001 Correct Response: D. The total number of stickers is 1,125, so x times y times z = 1,125. The prime factorization of 1,125 is . 3 squared times 5 cubed These factors may be grouped in different ways to form the numbers x, y, and z (e.g., x = 15, y = 5, z = 15; x = 25, y = 9, z = 5). For every grouping, each number must be either 3, 5, or a product of powers of those numbers, which leads to the result that all three numbers are odd (i.e., 3 is odd, 5 is odd, and any product formed from odd factors like 3 times 5 squared is also odd). Incorrect Response: A. The prime factorization of 1,125 is . 3 squared times 5 cubed Since there are no factors of 2 in the prime factorization, 1,125 cannot have any even factors. Incorrect Response: B. The prime factorization of 1,125 is . 3 squared times 5 cubed Since there are no factors of 2 in the prime factorization, 1,125 cannot have any even factors. Incorrect Response: C. The prime factorization of 1,125 is . 3 squared times 5 cubed Since there are no factors of 2 in the prime factorization, 1,125 cannot have any even factors. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | D |
Objective 001 Correct Response: D. In this response, a = negative 2, b = negative 1, c = negative 2. The first condition a is less than or equal to b is satisfied since negative 2 is less than or equal to negative 1 and the second condition b is greater than c is satisfied since . negative 1 is greater than negative 2 Incorrect Response: A. In this response, a = 1, b = 1, c = 2. While the first condition a is less than or equal to b is satisfied since 1 is less than or equal to 1 the second condition b is greater than c is not: . 1 is less than 2 Incorrect Response: B. In this response, a = negative 3, b = negative 2, c = 1. While the first condition a is less than or equal to b is satisfied since negative 3 is less than or equal to negative 2 the second condition b is greater than c is not: . negative 2 is less than 1 Incorrect Response: C. In this response, a = negative 1, b = negative 2, c = 3. The first condition a is less than or equal to b is not satisfied by these values: . negative 1 is greater than or equal to negative 2 The second condition is also false: . negative 2 is greater than 3 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | B |
Objective 002 Correct Response: B. Point G represents the third value when the list is written in ascending order: 0.250, 0.252, 0.255, 0.259. The value of 0.255 corresponds to Sheet 2 in the table. Incorrect Response: A. This response represents point E on the number line, since 0.25 = 0.250. Incorrect Response: C. This response represents point H since 0.259 is the value closest to 0.260. Incorrect Response: D. This response represents point F since 0.252 is the second lowest value in the table. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | C |
Objective 002 Correct Response: C. Let the thousandths place digit be A, A times 1 over 1000 equals a times 10 to the negative third power and the hundredths place digit be B, . B times 1 over 100 equals b times 10 to the negative second power The product of these numbers is . A times 10 to the negative third power times b times 10 to the negative second power is equal to a times b times 10 to the negative fifth power If the product of A and B is less than 10, then the smallest place value that can contain a nonzero digit in the product is the hundred-thousandths place. Incorrect Response: A. This response could be chosen if incorrect powers of 10 were used to describe the smallest place value for each decimal. Incorrect Response: B. This response could be chosen if incorrect powers of 10 were used to describe the smallest place value for each decimal. Incorrect Response: D. This response could be chosen if incorrect powers of 10 were used to describe the smallest place value for each decimal. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | B |
Objective 002 Correct Response: B. The distributive property was used to divide each addend by 20: . The quantity 400 plus 20 plus 6 divided by 20 equals 1 twentieth times the quantity 400 plus 20 plus 6 which equals 400 divided by 20 plus 20 divided by 20 plus 6 divided by 20 which equals 20 plus 1 plus 3 tenths Incorrect Response: A. The associative property of addition is used to rewrite 426 into expanded form. Incorrect Response: C. The commutative property is used to change the order in which expressions are added or multiplied. Incorrect Response: D. The multiplicative identity property is used to reduce the fraction 6 twentieths : . 6 twentieths is equal to the quantity 3 times 2 divided by the quantity 10 times 2, which is equal to 3 tenths times 2 over 2, which is equal to 3 tenths |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | A |
Objective 002 Correct Response: A. Let the regular price of a shirt be x. The regular price of two shirts is 2x, but the customer only pays a price of 1.5x for these shirts because they buy the first one at price x and the second one at price 0.5x. This represents a discount of 25 percent since 0.5 x divided by 2.0 x = 0.25. Incorrect Response: B. This response may be chosen by comparing the discount to the sale price and then rounding: . 0.5 x divided by 1.5 x equals 0.3 repeating or approximately 33 percent Incorrect Response: C. This response may be chosen if the half-off sale is incorrectly applied to both items. Incorrect Response: D. This response represents the percent of the regular price that the customer pays for the two shirts. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | D |
Objective 002 Correct Response: D. The correct response can be found by calculating the concrete use as shown: 0.05 plus one fifth equals 0.05 plus 0.20 which equals 0.25 Incorrect Response: A. This response may be the result of misinterpreting the value of 1 fifth to be 0.02, which would lead to the equation 0.05 + 0.02 = 0.07. Incorrect Response: B. This response could be the result of misinterpreting 5 percent to be equal to 0.5 and multiplying instead of adding: 0.5 times 0.2 = 0.10. Incorrect Response: C. This response represents the percent of the original supply of concrete that was used on Tuesday:
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | B |
Objective 002 Correct Response: B. The left model shows 56 over 100 = 0.56 and the right model shows 2 tenths = 0.20. The difference of these two values is 0.36. Incorrect Response: A. This response could be the result of taking the difference between the area of the white region on the left square, 0.44, and the area of the gray region on the right square, 0.2. Incorrect Response: C. This response could be the result of misinterpreting the difference to be 0.44 minus 0.02. Incorrect Response: D. This response could be the result of misinterpreting the difference to be 0.56 minus 0.02. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | C |
Objective 002 Correct Response: C. The number line has tick marks that divide the distance between 0 and 1 into quarters. Point P is closer to the second quarter than the first quarter (0.50) and point Q is very close to the third quarter (0.75). The values P = 0.42 and Q = 0.77 are consistent with this information in the number line. Incorrect Response: A. The number line has tick marks that divide the distance between 0 and 1 into quarters. Point P is between the first and second quarter (0.25 is less than P is less than 0.50) and point Q is between the third and fourth quarters (0.75 is less than Q is less than 1). Incorrect Response: B. Point P could represent the value 0.40, but Q cannot represent 0.70 because it must be greater than 0.75. Incorrect Response: D. The location for point P in the diagram is plausible, but the location of point Q is much too close to 0.75 to accurately represent the value 0.92. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | D |
Objective 002 Correct Response: D.
1 eleventh equals 0 point 0 9 repeating Multiplying this unit fraction by any whole number from 1 to 10 produces a decimal that repeats in a similar fashion using multiples of 9 Incorrect Response: A. This claim can be disproven by considering n = 4. 4 elevenths equals 0 point 3 6 repeating Incorrect Response: B. This claim can be disproven by considering n = 4. 4 elevenths equals 0 point 3 6 repeating Incorrect Response: C. This claim can be disproven by considering n = 1. 1 elevenths equals 0 point 0 9 repeating |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | A |
Objective 002 Correct Response: A. Any simplified fraction p over q may be written as p times the fraction 1 over q and the decimal equivalent of p over q will only terminate if 1 over q terminates. This happens when q has no prime factors other than 2 and 5, because only powers of these values or their products (e.g., 2, 5 squared = 25, 2 squared times 5 cubed = 500) divide 1 without producing a repeating decimal. (If p over q is a terminating decimal, then P over q times 10 to the power of x will produce an integer for some whole number x.) Incorrect Response: B. Consider counterexamples, such as 3 fifths and . 7 eighths These numerators are divisible by 3 and 7, respectively, and the fractions are equivalent to the terminating decimals 0.60 and 0.875, respectively. Incorrect Response: C. Consider a counterexample, such as , 4 fifths which is equal to 0.80. Incorrect Response: D. Consider a counterexample, such as , 3 fourths which is equal to 0.75. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | C |
Objective 002 Correct Response: C. The regular price of the refrigerator is 755 dollars and the sale price is . 755 dollars times 0.8 When the shopper rounds the price up, the estimated sale price becomes . 800 dollars times 0.8 The difference between the estimate and the sale price is . 800 dollars times 0.8 minus 755 dollars times 0.8 equals the quantity 800 dollars minus 755 dollars times 0.8 equals 45 dollars times 0.8 equals 36 dollars Incorrect Response: A. This response represents the difference between the actual and estimated discount: The quantity 800 times 0.2 minus the quantity 755 times 0.2 equals 160 minus 151 equals 9 Incorrect Response: B. This response represents the result of finding 20 percent of the difference between the list price of the refrigerator and the estimate rounded down to the nearest hundred: The quantity 755 minus 700 times 0.2 equals 55 times 0.2 = 11. Incorrect Response: D. This response represents the difference between the actual and estimated discount after rounding the value of 755 dollars down to 700 dollars : The quantity 755 minus 700 times 0.8 = 44. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | A |
Objective 002 Correct Response: A. The operation of subtraction can be used to determine how much greater one quantity is than another. The difference between the length of the humerus and the length of the human hand is 36.46 minus 18.9 = 17.56. Incorrect Response: B. This response could be the result of subtracting 36.46 minus 18.09. Incorrect Response: C. This response could be the result of a regrouping error where the 3 (representing 30 in 36.46) is incorrectly grouped as 3 tens and 10 ones (rather than 2 tens and 10 ones), as follows:
The standard subtraction algorithm is shown for the problem 36.46 minus 18.90, in which a regrouping error is shown. The 6 in 36 is rewritten as a 15 and the 4 in 36.46 is rewritten as 14. The product in this case is shown to be 27.56. Incorrect Response: D. This response applies the regrouping error described in the rationale for Incorrect Response C to both the digits 3 and 6 in 36.46.
The standard subtraction algorithm is shown for the problem 36.46 minus 18.90. The 6 in 36 is rewritten as a 16 to produce the difference 28.56. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | C |
Objective 002 Correct Response: C. 42 percent of the pancake batter is flour. This percentage does not change when the person doubles the recipe to 600 grams: 0.42 times 600 = 252 grams. Incorrect Response: A. This response may be the result of thinking that 42 percent is to be doubled to 84 and taken as the answer. Incorrect Response: B. This response represents the amount of flour used in 300 grams of pancake batter: 300 times 0.42 = 126. Incorrect Response: D. This response may be the result of thinking that doubling the pancake batter implies that the percentage of flour in the mix is also doubled: 2 times 0.42 times 600 equals 0.84 times 600 = 504. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | B |
Objective 002 Correct Response: B. If r is regular price, 0.6r is sale price during the first week. Each subsequent week, the clothing is discounted by 10%, which can be done by multiplying the expression 0.6r by 0.9 for each week of the sale. The price during week 3 can be calculated using the expression . 0.6 r times 0.9 squared equals 0.486 r Incorrect Response: A. This expression is the result of misinterpreting the initial sale price of the clothing and multiplying 0.4r times . 0.9 squared Incorrect Response: C. This response represents the total amount that the original price has been discounted, not the price itself: R minus the quantity 0.6 r times 0.9 squared equals r minus 0.486 r = 0.514r. Incorrect Response: D. This response may be the result of misinterpreting the original sale price as 0.40r and then misrepresenting the sale price of the clothing on subsequent weeks as being 10 percent of that price: R minus the quantity 0.4 r times 0.1 squared equals 0.996 r |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | C |
Objective 003 Correct Response: C. This response uses equal-sized rectangles to represent each box when it is full of bars. It also shows that the removal of 21 honey bars and 32 raisin bars leaves the honey box with twice as many bars compared to the raisin box. Incorrect Response: A. This response does not make any reference to the number of bars that were eaten or to the number of bars in each of the full boxes. Instead, it represents the number of eaten honey bars, 21, as being equal to half of the remaining number of honey bars and equal to all the remaining number of raisin bars. This is not consistent with this situation. Incorrect Response: B. This response reverses the relationship between the ratio of the leftover bars, and it does not account for the bars that have already been eaten. Incorrect Response: D. This response reverses the relationship between the ratio of the leftover bars. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | B |
Objective 003 Correct Response: B. The division 11 divided by 4 can be interpreted to mean the number of groups of 4 that are needed to make 11. Two whole groups of 4 makes 8; another 3 objects ( 3 fourths of a full group) are still needed to make 11. Another way to identify the significance of the remainder is to represent the division using fractions: 11 fourths is equal to four fourths plus four fourths plus 3 fourths which is equal to 2 and 3 fourths Incorrect Response: A. For the division algorithm, a remainder can be represented as a fraction of the form . Remainder divided by divisor This response reflects the misconception that the remainder can be represented as . Remainder divided by quotient Incorrect Response: C. For the division algorithm, a remainder can be represented as a fraction of the form . Remainder divided by divisor This response reflects the misconception that the remainder can be represented as . Quotient divided by remainder Incorrect Response: D. For the division algorithm, a remainder can be represented as a fraction of the form . Remainder divided by divisor This response reflects the misconception that the remainder can be represented as . Devisor divided by remainder |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | C |
Objective 003 Correct Response: C. Since the two fractions are equal, the product can be found using a proportion: X over 4 equals 6 over y implies 4 times x over 4 equals 6 over y times 4 implies x equals 24 over y, which implies the product of x and y is 24 Incorrect Response: A. This response may be the result of a misconception that the proportion X over 4 equals 6 over y has a property that the sums of opposite numerators and denominators are equal (e.g., that an equivalent of cross products exists with addition). Incorrect Response: B. This response represents the least common multiple of 4 and 6. Incorrect Response: D. This response could be the result of the misconception that fractions are equivalent if their numerator and denominator differ by the same amount. If that difference is taken to be 1, then the fractions are supposed to be 5 fourths and 6 fifths |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | A |
Objective 003 Correct Response: A. The expression 30 divided by 8 represents the number of pizzas required to feed 30 students if each student has 1 slice and each pizza is cut into 8 slices (3.75 pizzas total). The expression The quantity 30 times 2 divided by 8 represents the number of pizzas required to feed 30 students if they each have 2 slices of pizza (7.5). Since one third of students want cheese pizza and the remaining students want pepperoni pizza, it follows that two thirds of the pizzas need to be pepperoni pizzas. The number of pepperoni pizzas needed is 2 thirds of the total number of pizzas needed: The quantity 30 times 2 divided by 8 times the fraction 2 thirds Incorrect Response: B. This response may be the result of the misconception that the fraction representing the total number of pizzas needed, The quantity 30 times 2 divided by 8 can be divided by 1 third to find the result. (Since dividing by a fraction is the same as multiplying by the reciprocal, dividing by 1 third triples the number of pizzas needed.) Incorrect Response: C. This response represents the number of cheese pizzas that are needed, not the number of pepperoni pizzas. Incorrect Response: D. This response may be the result of the misconception that the fraction representing the total number of pizzas needed, , The quantity 30 times 2 divided by 8 can be divided by 2 thirds to find the result. (Since dividing by a fraction is the same as multiplying by the reciprocal, dividing by 2 thirds increases the total number of pizzas needed by a factor of one half.) |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | A |
Objective 003 Correct Response: A. The combined weight of the art pieces can be found by evaluating the expression
9 plus 5 sixths times 9 plus 4 fifths (5 in denominator is crossed out) times 5 sixths (5 in numerator is crossed out) times 9 is equal to 9 plus 45 sixths plus 2 thirds times 9 is equal to 9 plus 7 and one half plus 6 which is equal to 22 and 1 half Incorrect Response: B. This response may be the result of misinterpreting the combined weight of the art pieces to 9 plus 5 sixths times 9 plus 4 fifths times 9 Incorrect Response: C. This response may represent a misinterpretation of the combined weight of the art pieces as well as a miscalculation in the sum 9 plus 5 sixths plus 9 plus 4 fifths plus 9 (adding the numerators and denominators without finding a common denominator). Incorrect Response: D. This response may represent a misinterpretation of the combined weight of the art pieces as 9 plus 5 sixths plus 9 plus 4 fifths plus 9 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | D |
Objective 003 Correct Response: D. In the image shown, x, y, and z represent the missing values in the table.
The table from the stem is shown with an x representing the digit in the tens place for the payment, y representing the digit in the tens place for the number of monthly payments, and z representing the digit in the ones place for the number of monthly payments. Since 5y = 150, y must equal 30. If y = 30, then x y = 600 implies that x = 600 divided by 30 = 20. 20 z must equal 120, which implies that z = 120 divided by 20 = 6. Since y = 30 and z = 6, the total number of monthly payments is equal to y + z or 36. Incorrect Response: A. This value represents the amount of each monthly payment, not the number of monthly payments. Incorrect Response: B. This response is the result of adding two of the missing values diagonally in the table (x and z in the image shown in the rationale for Correct Response D). Incorrect Response: C. This response is the result of adding two of the values diagonally in the table (y and 5 in the image shown in the rationale for Correct Response D). |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | D |
Objective 003 Correct Response: D. This response represents the product of 50 and 240, which is the result of correctly rounding each value to the nearest tens place: 50 times 240 = 12,000. Incorrect Response: A. This response is the result of rounding the values down to the nearest ten in the estimate: 40 times 230 = 9,200. Incorrect Response: B. This response may be the result of incorrectly rounding the value of 46 to 40 in the estimate: 40 times 240 = 9,600. Incorrect Response: C. This response may be the result of incorrectly rounding the value of 237 to 230 in the estimate: 50 times 230 = 11,500. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | C |
Objective 003 Correct Response: C. The estimated value is the sum of three values that are rounded up to the nearest tenth. The difference between the estimated sum and the actual sum is maximized when the value of the money in each pile has a "5" in the hundredths place, which results in a difference of 3 times 5 cents or 15 cents . Incorrect Response: A. This value represents two piles being rounded up by 5 cents and one pile being rounded by 0 cents. It is not the greatest possible error. Incorrect Response: B. This value represents the three piles being rounded up by 4 cents. It is not the greatest possible error. Incorrect Response: D. This value could represent the sum of rounding three piles of coins up by 6 cents. This may reflect a misunderstanding about when to round a value up instead of down. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | B |
Objective 003 Correct Response: B. The total volume of the fudge in the tray is equal to 12 times 15 times 1 = 180 cubic inches. Since 20 cubic inches of fudge equals one pound, the total weight of the fudge in the tray is 180 divided by 20 = 9 lbs. The number of pieces of fudge can be found by dividing the total weight of the fudge in the tray by the weight of each individual piece: 9 divided by 1 sixteenth equals 9 times 16 which equals 144 Incorrect Response: A. This response may be the result of misinterpreting the information and using the calculation The quantity 16 times 20 minus the quantity 12 times 15 = 140. Incorrect Response: C. This response represents the total volume of the fudge in the tray in cubic inches, not the number of pieces that can be formed using that volume. Incorrect Response: D. This response may be the result of misinterpreting the information and using the calculation . The quantity 12 times 15 divided by 1 twentieth all divided by 16 is equal to 225 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | B |
Objective 003 Correct Response: B. The order of operations ( P E M D A S ) implies that first priority when evaluating this expression is simplifying the exponential term (since there are no operations to complete within parentheses): The quantity negative 5 squared equals negative 5 times negative 5 which equals 25, which implies negative 3 halves divided by 25 The second operation that appears in the expression is division, and since dividing by a fraction is the same as multiplying by the reciprocal, Negative 3 halves divided by 25 equals negative 3 halves times 1 twenty-fifth which equals negative 3 fiftieths Incorrect Response: A. This response may be the result of misinterpreting the order of operations and simplifying the expression The quantity negative 3 halves times 5 squared is equal to the quantity negative 3 tenths squared and then making an error with the sign when squaring the fraction. Incorrect Response: C. This response may be the result of a sign error when applying the order of operations (interpreting the value of negative 3 halves as positive at some point in the process), or misinterpreting the value of . the quantity negative 5 squared Incorrect Response: D. This response may be the result of incorrectly multiplying the denominator of the fraction negative 3 halves by the whole number 5 and simplifying the expression as shown: The quantity negative 3 halves times 5 squared equals the quantity negative 3 tenths squared equals 9 hundredths |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | B |
Objective 003 Correct Response: B. The length of segment d is the sum of the distances that a and b are from zero on the number line. The absolute value of b gives the distance that b is from zero on the number line, and The absolute value of a gives the distance that a is from zero on the number line, so the sum The absolute value of a plus the absolute value of b gives the total length of segment d. Incorrect Response: A. This response is the result of a misconception involving absolute value. If a is positive and b is negative, then the sum has a value that is less than the total distance between a and b on the number line. Incorrect Response: C. Since b is negative and a is positive, the sum a + b will produce a value that is less than the total distance between the endpoints. Incorrect Response: D. The length of segment d is the combined distance from b to 0 and from 0 to a. These distances are combined with addition and not subtraction. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | A |
Objective 003 Correct Response: A. Finding one fourth of a quantity is the same as dividing it by 4 or multiplying it by one fourth. The amount of paint that was used to paint the wall can be found by multiplying the initial amount of paint, 2 and 1 half by . 1 fourth Incorrect Response: B. The cyclist travels 2 and 1 half miles in one quarter of an hour, or . 2 and 1 half miles divided by one fourth of an hour Then the speed of the cyclist, in miles per hour, is four times that quantity: . 2 and 1 half divided by 1 fourth equals 2 and 1 half times 4 Incorrect Response: C. Consider a rectangle with side lengths a and b. The area of the rectangle is a times b which is equal to 2 and 1 half in this context. If one dimension, a, is equal to , 1 fourth then 1 fourth times b equals 2 and 1 half which implies b equals 2 and 1 half divided by 1 fourth Incorrect Response: D. Like response C, this problem implies division. The total number of quarter cup portions in 2 and 1 half cups of chocolate chips is equal to 2 and 1 half divided by one fourth |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | A |
Objective 003 Correct Response: A. This equation rewrites the original expression using mathematical concepts, the first of which is the fact that a fraction like 2 and 3 fourths is equal to 2 + . 3 fourths The commutative and associative properties of addition are then applied to add the whole number values first and the fractional values second. Incorrect Response: B. This response represents a misconception related to the distributive property of multiplication for the expression The quantity 2 plus 3 fourths times the quantity 3 plus one third Incorrect Response: C. Consider the following property of division for c + d is not equal to 0: . The quantity a plus b divided by the quantity c plus d is equal to a divided by the quantity c plus d plus b divided by the quantity c plus d To apply this property correctly to the expression in this response, let a = 2 and b = , 3 fourths divide both a and b by 3 , and 1 third and then add their quotients together. This response is incorrect because it shows only a being divided by 3 and b being divided by . 4 radical x Incorrect Response: D. This response represents a misconception (sign error) with using the distributive property for subtraction. The following equation corrects the error: The quantity 2 plus 3 fourths minus the quantity 3 plus 1 third equals the quantity 2 plus 3 fourths plus the quantity negative 3 minus 1 third equals the quantity 2 minus 3 plus the quantity 3 fourths minus 1 third |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | D |
Objective 004 Correct Response: D. The fence is a square enclosure with an area of x square feet. Therefore, the side length of the fence is Radical x and its total perimeter is . 4 Radical x Because the information states that the perimeter of the fence is equal to y, y = . 4 Radical x Incorrect Response: A. The equation y = 2x describes a linear equation with a y-intercept of 0 and a slope of 2. This line passes through points such as (1, 2), (2, 4), and (3, 6). The graph in the stem is not linear, so this equation is incorrect. Incorrect Response: B. The equation y = Radical x + 6 describes a square root function that increases in a way that is similar to the graph shown (in that the correct response is a square root equation) but has a y-intercept at the point (0, 6), which is inconsistent with the y-intercept shown in the graph. Incorrect Response: C. This response can be eliminated by considring that it predicts a perimeter of negative 7 for an area of 1, which is inconsistent with the values shown in the graph and makes no sense for this context. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | D |
Objective 004 Correct Response: D. This function generates the correct values since each output, f of x is equal to the reciprocal of the square of the input, x:
Incorrect Response: A. This function would generate the following values:
Incorrect Response: B. This function would generate the following values:
Incorrect Response: C. This function would generate the following values:
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | A |
Objective 004 Correct Response: A. The function machine applies two operations to produce the output (subtract the input by 2, then square that value). These rules produce a positive output for an input of 0, an output of 0 for an input for 2, and positive outputs for inputs greater than 2. This graph is consistent with that information. Incorrect Response: B. This graph always grows more slowly as input values increase, which is not consistent with the squaring operation. Consider that the given rules of the function machine match the input values of 2, 12, and 22 to the output values of 0, 100, and 400, respectively. Incorrect Response: C. This graph shows output values always increasing with increasing input values. This is not consistent with the rules for the function machine for input values less than 2: the input value 0 has an output value of 4 and the input value of 1 has an output value of 1. The output values only begin to increase when the input values exceed 2. Incorrect Response: D. This graph lacks the properties described in the correct response. Consider that the given rules of the function machine match the input values of 2, 12, and 22 to the output values of 0, 100, and 400, respectively. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | C |
Objective 004 Correct Response: C. The given information states that the mass needed to balance a 30-gram mass is inversely proportional to its distance from the fulcrum. This means that m x = k, where k is a constant. Substituting the values given in the problem yields 30 times 60 = 1,800 = k. If x is changed to 20, then M times 20 equals 1,800, which means m = 90. Incorrect Response: A. This response is the result of the misconception that mass is proportional to the distance from the fulcrum, rather than inversely proportional. Incorrect Response: B. This is the result of misinterpreting the question and identifying the distance between the fulcrum and m, rather than the mass needed to balance the board. Incorrect Response: D. This response is the correct mass needed to balance the board when x is 15 centimeters (one fourth the starting distance) from the fulcrum. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | D |
Objective 004 Correct Response: D. The total number of triangles in any figure of the pattern can be represented by the expression 4 n squared where n is the figure number. Since one of the four triangles in each square is shaded, there are a total of One fourth times 4 n squared equals n squared shaded squares in each figure. The number of unshaded squares can be determined by finding the difference: 4 n squared minus n squared equals 3 n squared The seventh figure in the pattern has a total of 3 times 7 squared = 147 unshaded triangles. Incorrect Response: A. This response may represent the misconception that the number of unshaded triangles in a figure is equal to n squared : 7 squared = 49. Incorrect Response: B. This response may represent the misconception that the number of unshaded triangles is equal to 3 to the fourth power = 81. Incorrect Response: C. This represents the number of unshaded triangles in the sixth figure in the pattern: 3 times 6 squared = 108. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | B |
Objective 004 Correct Response: B. The poured water increases ever more slowly in height as it fills the container from its base to its widest point. Where the container narrows in its middle region, the height of the poured water increases ever more quickly until it reaches the top section of the container. That final section has a short height and a constant, narrow width, so the water fills relatively quickly and at a constant rate. The graph in this response best represents these changes. Incorrect Response: A. This response shows the height of the water in the container to be increasing at an increasing rate, which is not true for the initial shape of the container. Incorrect Response: C. The horizontal stretch in the graph suggests that water is being poured in without changing its height in the container. This will not happen with the container shown. Incorrect Response: D. The horizontal stretch in the graph suggests that water is being poured in without changing its height in the container. This will not happen with the container shown. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | C |
Objective 004 Correct Response: C. This scenario is correct because it describes the cyclist's movement in a way that is consistent with the graph:
Incorrect Response: A. The first sentence of this scenario implies that the graph should pass through the point (20, 3) since the bicyclist has traveled a total of 3 miles in 20 minutes. The graph shown does not pass through this point. Incorrect Response: B. This scenario is consistent with the graph shown from the origin to x = 30, but at that point, the graph shows a horizontal line (which implies that the bicyclist has stopped). This scenario describes the cyclist traveling along a side road at that point, which would mean that the cyclist's distance from home would not be constant in that interval. Incorrect Response: D. This scenario states that the bicyclist has traveled 3 miles in 30 minutes, which implies the graph should pass through the point (30, 3). The graph shown does not pass through this point, so the scenario is not accurate. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | C |
Objective 005 Correct Response: C. Evaluating the expression for x = 2 requires careful interpretation of the negative signs and the exponents: 3 times the quantity negative 2 to the negative first power minus the quantity negative 2 cubed equals 3 times the quantity negative one half minus the quantity negative 8 equals negative 3 halves plus 8 equals negative 1 and 1 half plus 8 equals 6 and 1 half. Incorrect Response: A. An error related to the sign for the value of The quantity negative 2 cubed could lead to this result. Interpreting the value to be 8 leads to the expression Negative 3 halves minus 8 = negative 9 and 1 half Incorrect Response: B. This response may be the result of misinterpreting the value of 3 times the quantity negative 2 to the negative first power to be negative 1 sixth and making a sign error when interpreting The quantity negative 2 cubed : negative 1 sixth minus 8 equals negative 8 and 5 sixths Incorrect Response: D. This response may be the result of misinterpreting the value of 3 times the quantity negative 2 to the negative first power to be |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | B |
Objective 005 Correct Response: B. In the equation Q times t = V, Q is directly proportional to V (e.g., doubling flow rate Q for a given amount of time will double volume V) and inversely proportional to t (e.g., doubling the flow rate Q and halving the time allows the same volume of water to pass through the pipe). In general, two variables are directly proportional when they are in a proportional relationship and inversely proportional when their product is constant. Incorrect Response: A. This equation shows that Q is inversely proportional to V since Q = . t divided by v (This implies that the value of Q decreases as the value of V increases.) Incorrect Response: C. This equation shows that Q is directly proportional to both t and V (because Q = v times t ). Incorrect Response: D. This equation shows that Q is inversely proportional to both t and V (because Q times v times t = 1). |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | D |
Objective 005 Correct Response: D. Applying the distributive property and then combining like terms produces the following result: . 8 x minus 5 times the quantity x minus 1 plus 3 x equals 8 x minus 5 x plus 5 plus 3 x This further simplifies to = 6x + 5. 3 x plus 5 plus 3 x equals 6 x plus 5 Incorrect Response: A. This response is the result of sign errors with the distributive property, as well as errors with distributing the factor of negative 5 to the negative 1 in the quantity . X minus 1: 8 x plus 5 x minus 1 plus 3 x equals 10 x minus 1 Incorrect Response: B. This response is the result of forgetting about the factor 3x at the end of the expression: . 8 x minus 5 x plus 5 equals 3 x plus 5 Incorrect Response: C. This response is the result of not distributing the factor of negative 5 to the negative 1 in the quantity . X minus 1: 8 x minus 5 x minus 1 plus 3 x equals 3 x minus 1 plus 3 x equals 6 x minus 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | C |
Objective 005 Correct Response: C. Solving the equation for n yields the following result: Y equals x plus d n minus d implies y equals x plus d times the quantity n minus 1 implies y minus x equals d times the quantity n minus 1 implies the quantity y minus x divided by d equals n minus 1 implies n equals 1 plus the quantity y minus x divided by d. Incorrect Response: A. This response may be the result of sign errors along with a misconception that the two values of d in the initial equation can be combined to form 2d. Incorrect Response: B. This response represents misconceptions about what it means to "move" a variable from one side of the equal sign to another. (This may be the result of moving the variables without regard to the addition property of equality.) Incorrect Response: D. This response may be the result of a sign error when moving one value of d to the left with y, and then dividing both sides by x minus d which could be the result of a misinterpretation of the order of operations in the problem. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | A |
Objective 005 Correct Response: A. The double shaded region in the graph below describes all the possible combinations of Cruisers and Racers that the company may develop without exceeding 24 total bicycles (i.e., where x + y is less than or equal to 24) and without exceeding 160 total hours of labor (i.e., where 8x + 4y is less than or equal to 160).
A graph is shown in the first quadrant of the coordinate plane such that the horizontal axis represents the number of racers and the vertical axis represents the number of cruisers. The graph shows the shaded region defined by the inequalities x plus y is less than or equal to 24 and 8 x plus 4 y is less than or equal to 160. Incorrect Response: B. This response shows the solution to the system of inequalities x + y is less than or equal to 24 and y is less than or equal to 20. The inequality y is less than or equal to 20 may be the result of dividing 160 by 8. Incorrect Response: C. This response shows the solution to the system of inequalities x + y is less than or equal to 24 and x is less than or equal to 12. The inequality x is less than or equal to 12 may be the result of adding 4 and 8. Incorrect Response: D. This response is the graph of the inequality x + y is less than or equal to 24, which is only one of the inequalities used to solve the system. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | D |
Objective 006 Correct Response: D. The ratio of the investments shown in the table X to Y to Z is equal to 750 to 500 to 250 or 3 to 2 to 1. The total investment is equal to 2,100 dollars so we can use the equation 3 x plus 2 x plus x equals 2,100 to determine the investment in Company Z: 3 x + 2 x + x = 2,100 implies 6 x = 2,100 implies x = 350 This means the investor may invest 350 dollars in Company Z, twice that amount 2 times 350 = 700 dollars in Company Y, and triple that amount 3 times 350 = 1,100 dollars in Company X. Incorrect Response: A. This response maintains the same ratio between the companies as the table, but the sum of the investments is not equal to 2,100 dollars Incorrect Response: B. In this response, the second investor spends a total of 2,100 dollars by investing 200 dollars more than what the first investor allocated for each of the companies. This addition does not keep the ratios equal. For example, The sum 750 dollars plus 200 dollars divided by the sum 500 dollars plus 200 dollars equals 950 dollars divided by 700 dollars which is not equal to 750 dollars divided by 500 dollars. Incorrect Response: C. In this response, the ratio comparing the investment in Company X to the investment in Company Z is 1,050 dollars divided by 700 dollars is equal to 3 divided by 2 However, the table shows that the ratio of these investments is actually 750 dollars divided by 250 dollars is equal to 3 divided by 1 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | B |
Objective 006 Correct Response: B. The unit rate (i.e., the cost for one muffin) can be found by the equation 13.5 divided by 3 = 4.50. The missing value in the table corresponds to the price for 5 muffins, which is 5 times the unit rate: 4.50 times 5 = 22.50. Incorrect Response: A. This response is the result of interpreting 5 to be 2 fifths of the distance from 3 to 8, which may lead to the calculation 13.50 + 13.50( 2 fifths ) = 13.50 + 5.40 = 18.90. Incorrect Response: C. This response is the result of finding the average of the costs shown in the table: The sum of 13.50 and 36.00 divided by 2 is equal to 49.50 divided by 2 which is equal to 24.75 This would imply that the price for each muffin is 4 dollars and 95 cents which is not equal to 13.5 divided by 3 = 4.50. Incorrect Response: D. This response may be the result of misinterpreting the unit cost for a muffin to be 1 dollar then subtracting 3 dollars from the value of . 36 dollars This is inconsistent with the unit price of 13.5 divided by 3 = 4.50 per muffin. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | C |
Objective 006 Correct Response: C. If the 12 kittens represent 2 thirds of the cats, then the total number of cats can be found using the proportion . 2 thirds equals 12 divided by x which implies x equals 18 Since 25 percent of the animals at the shelter are cats, the total number of animals can be found using the percent proportion 25 divided by 100 equals 18 divided by a Incorrect Response: A. This response is the result of misinterpreting the total number of cats to be 8 ( 2 thirds of 12). This contradicts the given information that there are 12 kittens at the animal shelter. Incorrect Response: B. This response is the result of misinterpreting the total number of cats to be 8 ( 2 thirds of 12) and then setting up the percent proportion incorrectly. This gives the result that there are only 2 animals at the shelter. Incorrect Response: D. This is the result of correctly identifying the number of cats at the shelter but then setting up the final percent proportion incorrectly. This response gives a total of 4.5 animals at the shelter. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | D |
Objective 006 Correct Response: D. Using the similarity statement provided, we can conclude that P Q is similar to M N and . R Q is similar to O N We can calculate PQ by setting up a proportion where the ratios compare the lengths of the segments within each triangle: P Q divided by R Q is equal to M N divided by O N implies P Q divided by 108 is equal to 19 divided by 27 Incorrect Response: A. This response is likely the result of misinterpreting the similarity statement shown in the stem. This could lead to the construction of an invalid proportion. Incorrect Response: B. This response is likely the result of misinterpreting the similarity statement shown in the stem. This could lead to the construction of an invalid proportion. Incorrect Response: C. This response is likely the result of misinterpreting the similarity statement shown in the stem. This could lead to the construction of an invalid proportion. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | D |
Objective 006 Correct Response: D. When two variables vary directly, the ratio between them always stays the same. In this equation, the dependent variable (y) is always 7 times the independent variable (x). Incorrect Response: A. In this equation, x and y are inversely related. The ratio between x and y does not stay the same for different inputs for this equation. (Consider the input/output pairs x = 1, y = 2 and x = 8, y = .) 1 fourth Incorrect Response: B. This describes a linear equation with a constant rate of change and a y-intercept of 9, but a linear equation only describes direct variation when the y-intercept is 0. Incorrect Response: C. This equation is equal to y = , the expression x plus 1 all divided by x which describes a rational function. The values of x and y do not maintain the same ratio. (Consider the input/output pairs x = 1, y = 2 and x = 4, y = .) 5 fourths |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 55 | B |
Objective 006 Correct Response: B. In a proportion, cross products are equal:
R divided by s equals t divided by u implies u times r divided by s equals t divided by u (u in denominator is crossed out) times u (which is crossed out) implies u r divided by s equals t implies s (which is crossed out) times u r divided by s (s in denominator is crossed out) equals s t implies u r equals s t. Incorrect Response: A. This response may be the result of the misconception that diagonal sums are equal in a proportion. (For a counterexample, consider 1 half = 5 tenths : 1 + 10 is not equal to 5 + 2). Incorrect Response: C. This response represents the misconception that the sum of the numerators must be equal to the sum of the denominators in a proportion. (For a counterexample, consider 1 half = 5 tenths : 1 + 5 is not equal to 2 + 10.) Incorrect Response: D. This response represents the misconception that the product of the numerators must be equal to the product of the denominators in a proportion. (For a counterexample, consider 1 fourth equals 25 hundredths, but 1 times 25 is not equal to 4 times 100 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | A |
Objective 006 Correct Response: A. The 260-foot parcel is 1.3 times bigger in area than the 200-foot parcel (because The product 260 times 200 divided by the product 200 times 200 is equal to 13 tenths ). The price of this parcel must also be 1.3 times greater than the smaller parcel because it is directly proportional to the area. Therefore, the lot costs 24,000 dollars times 1.3 = 31,200 dollars Incorrect Response: B. This value represents the area, in square feet, of the 200-foot by 200-foot parcel. Incorrect Response: C. This value may be the result of using a 260-foot by 260-foot parcel in the calculations: The product of 260 times 260 divided by x is equal to the product 200 times 200 divided by 24 thousand, which implies 40 thousand x is equal to 1 billion 6 hundred 22 million 4 hundred thousand, which implies x is equal to 40 thousand 5 hundred 60 Incorrect Response: D. This value represents the area, in square feet, of the 200-foot by 260-foot parcel. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | A |
Objective 007 Correct Response: A. Assuming that the walkway is moving at a constant speed, we can find the rate of change using any two data points x 1 y 1 and x 2 y 2 in the table: . Y 2 minus y 1 divided by x 2 minus x 1 Using the points (0, 500) and (380, 1), the rate of change is equal to 500 minus 380 divided by 0 minus 1 is equal to negative 120 This means that the distance from the traveler to end of the walkway is decreasing by 120 feet per minute, which implies that the walkway is moving the traveler at a rate of 120 feet per minute. Incorrect Response: B. This response is the result using the data point (2, 260) to create the ratio 260 divided by 2 equals 130 divided by 1 Since the context refers to the distance from the end of the 500 foot walkway, the correct ratio is 500 minus 260 divided by 0 minus 2 equals 240 divided by negative 2 equals negative 120 Incorrect Response: C. This response may be the result of finding the average for the distance values in the table: 500 plus 380 plus 260 plus 140 divided by 4 equals 1,280 divided by 4 equals 320 Incorrect Response: D. This may be the result of misinterpreting the data point (1, 380) to represent the rate of change for the scenario. This would be true only if the data described the traveler's total distance traveled per minute, rather than their distance from the end of the walkway. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | A |
Objective 007 Correct Response: A. The initial rate for the machine is 36 divided by 2 = 18 pies per hour. The new rate is 240 divided by 8 = 30 pies per hour. The difference in the rates is equal to 30 minus 18 = 12. Incorrect Response: B. This response is the initial rate of production for the machine in the factory, not the difference in the rate of production. Incorrect Response: C. This response is the rate of production for the machine after the maintenance, not the difference in the rate of production. Incorrect Response: D. This response is the result of using the ratio 240 minus 36 divided by 8 minus 2 equals 204 divided by 6 = 34. This answer is not accurate because the scenario involves two different, constant rates of change. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | C |
Objective 007 Correct Response: C. The x-intercept for a line occurs when y = 0. To find the x-intercept for the linear equation shown, substitute 0 for y and solve for x: 3 x plus 2 times 0 equals 12 implies 3 x equals 12 implies x equals 4 Incorrect Response: A. This response may be the result of interpreting the coefficient for y in the given equation as the x-intercept for the line. Incorrect Response: B. This response may be the result of interpreting the coefficient for x in the given equation as the x-intercept for the line. Incorrect Response: D. This response represents the y-intercept for the given line: 3 times 0 plus 2 y equals 12 implies 2 y equals 12 implies y equals 6 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | D |
Objective 007 Correct Response: D. The solution to this problem can be found by replacing p with (p + 0.50) in the equation provided: D = negative 17,500 times the quantity p plus 0.50 plus 78,750 implies d equals negative 17,500 p minus 8750 plus 78,750 implies d equals negative 17,500 p plus 70,000 The new equation is 8,750 less than the original equation, which corresponds to a decrease in demand by 8,750 units. Incorrect Response: A. This response may be the result of misinterpreting the new equation D = negative 17,500 plus 70,000 The misconception may involve interpreting the y-intercept of the new equation as the change in demand. Incorrect Response: B. This response may be the result of a sign error when combining the constant terms in the equation D equals negative 17,500 times the quantity p plus 0.50 plus 78,750 (Accidentally using a minus sign instead of a plus sign after combining negative8,750 and 78,750 may lead to the conclusion that 70,000 implies a decrease in demand by 70,000 units.) Incorrect Response: C. This response may be the result of misinterpreting the given equation and the new equation D = negative 17,500 p plus 70,000 If D equals negative 17,500 p plus 78,750 is considered the new equation, it would appear to correspond to an increase in demand by 8,750 units. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | B |
Objective 007 Correct Response: B. The slope of each line represents the cost per mile for renting each truck. This information would allow someone to determine which truck is more reasonable for a given distance. Incorrect Response: A. The x-intercepts for each line would represent the number of miles each truck can be driven for 0 dollars so they are not in the domain for the functions in this context. Incorrect Response: C. The y-intercepts show the initial cost to rent each truck, but they do not provide information on the cost per mile to rent each truck. Incorrect Response: D. The intersection shows the number of miles for which the total cost of renting each truck is the same, but it does not provide information about the specific rate of change for each line. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | B |
Objective 007 Correct Response: B. The x-intercept for a line occurs when y = 0. To find the x-intercept for the given equation, substitute 0 for y and solve for x: 48 x equals 12 times 0 minus 17 minus 3 x implies 48 x equals negative 17 minus 3 x implies 51 x equals negative 17 implies x equals negative 1 third Incorrect Response: A. This may be the result of combining the like x terms to get 51 x and then dividing the coefficient by 17. Incorrect Response: C. This may be the result of an error when solving the equation for x, as well as an error when combining the like terms for x: 48 x minus 3 x = 45 x Incorrect Response: D. This response represents the y-intercept for the given equation: 48 times 0 equals 12 y minus 17 minus 3 times 0 implies 0 equals 12 y minus 17 implies 17 equals 12 y implies y equals 17 twelfths |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | B |
Objective 008 Correct Response: B. The volume of a cube, V, is equal to a side length, s, cubed: V = x cubed Since the volume of each cube is 8, . 8 equals s cubed implies the cube root of 8 equals the cube root of s cubed implies s equals 2 Exactly one face of each cube is touching the ground, and the area of one face of the cube is equal to length times width, or 2 times 2, which is equal to 4 square feet Since there are 25 boxes that each occupy 4 square feet of floor space, the total floor space for the configuration is 25 times 4 or 100 square feet Incorrect Response: A. This response may be the result of misinterpreting the side length of each box to be 1 foot : 1 squared times 25 = 25. Incorrect Response: C. This response may be the result of misinterpreting the side length of each box to be 4 feet : 4 squared times 25 = 400. Incorrect Response: D. This response may be the result of misinterpreting the side length of each box to be 8 feet : 8 squared times 25 = 1,600 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | C |
Objective 008 Correct Response: C. Consider the following diagram of equilateral triangle ABC:
Equilateral triangle A B C is shown. The midpoints of each side form a smaller inscribed equilateral triangle D E F such that D is the midpoint of A B, E is the midpoint of B C and F is the midpoint of A C. The larger equilateral triangle is divided by the inscribed triangle into four congruent triangles. The three bottom triangles are shaded gray. It follows from the information provided that D is the midpoint of A B and E is the midpoint of B C which implies A D is congruent to D B and B E is congruent to E C By using properties of special right triangles ( 30 60 90 degree formed by drawing an altitude in each of the smaller triangles), and properties of parallel lines ( D E is parallel to A C ), we can conclude that the four smaller triangles are congruent ( Triangle A D F is congruent to triangle D B E is congruent to triangle D E F is congruent to triangle F E C ). The ratio of unshaded triangles to shaded triangles is 1 to 3, which means the amount of paint necessary to finish the task is 1 third of what has already been used. Incorrect Response: A. This response may be the result of misinterpreting the triangles in the diagram shown in the rationale for Correct Response C by comparing the top triangle to the halves of the shaded equilateral triangles. This could lead to a ratio of 1 to 6. Incorrect Response: B. This response may be the result of misinterpreting the number of smaller triangles in the figure (i.e., each smaller triangle in the figure represents 1 fourth the area of the large triangle). Incorrect Response: D. This response may stem from the misconception that the painted area represents half of the triangle since the horizontal line segment is located halfway up the triangle. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | A |
Objective 008 Correct Response: A. Because of the relationship between the area of a triangle and the area of a rectangle with the same base
Incorrect Response: B. This response may be the result of the misconception that the two triangles (2 and 3) together represent 2 thirds of the total area of the rectangle. Incorrect Response: C. Because of the relationship between the area of a triangle and the area of a rectangle with the same base
Incorrect Response: D. The sum of the areas of triangles 1 and 2 is equal to 3 fourths of the total area of the rectangle, and the sum of the areas of triangles 4 and 6 is 1 half of the total area of the rectangle. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | B |
Objective 008 Correct Response: B. Adjacent angles are supplementary, which makes this a parallelogram and not necessarily a rhombus. (A rhombus must have 4 congruent sides.)
The interior angles for all the composing shapes for trapezoid W V Y U are shown. U W Z is equal to 30 degrees, and W Z U is equal to 60 degrees. Angles X W Z and X Y Z are equal to 60 degrees, and angles W Z Y and W X Y are equal to 120 degrees. Each interior angle for triangle X V Y is equal to 60 degrees. Incorrect Response: A. The claim that the four sides are congruent is not necessarily true. Incorrect Response: C. A rhombus has 4 congruent sides, congruent opposite angles, and supplementary adjacent angles. The information in the figure can only confirm the last two criteria (e.g., segment W X is not necessarily congruent to segment W Z Incorrect Response: D. The statement that a parallelogram must have four congruent sides is false. Quadrilateral W X Y Z is a parallelogram because its opposite angles are congruent. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | B |
Objective 008 Correct Response: B. Since the arc shown in the diagram has a 60 degree central angle, it must represent 60 divided by 360 equals 1 sixth of the total circumference for the circle. This means that the circumference of the circle is 6 times 4 = 24 feet Since the circumference of a circle is 2 pie r we can determine the length of the radius: 2 pie r equals 24 implies r equals 24 divided by 2 pie equals 12 divided by pie Substituting this value for r into the equation for the area of a circle yields the area: Pie r squared equals pie times the quantity 12 divided by pie squared equals pie times 144 divided by pie squared which equals 144 divided by pie square feet. Incorrect Response: A. This response may be the result of misinterpreting the radius to be 4 and then finding the circumference using that value: 2 pie r equals 2 times pie times 4 equals 8 pie Incorrect Response: C. This response may be the result of calculating the area of the circle using 4 as the radius: Pie r squared equals pie times 4 squared equals 16 pie Incorrect Response: D. This response gives the area of the circle excluding the
60 degree sector shown |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | C |
Objective 008 Correct Response: C. The net shown is for a square pyramid.
The cross-section described in this response creates an isosceles triangle where two legs are equal to the slant height of the pyramid:
The image indicates the cross section that is the result of a slice through the top vertex of the pyramid that is perpendicular to the base and parallel to one side of the base, resulting in a cross section that is the shape of an isosceles triangle. Incorrect Response: A. This response represents the shape of the cross section when the square pyramid is cut with a plane that is parallel to the square base:
The image indicates the cross section that is the result of a slice through the pyramid that is parallel to the base, resulting in a cross section that is the shape of a square. Incorrect Response: B. This response represents the shape of the cross section when the square pyramid is cut with a plane that is perpendicular to the base, intersects the base at a line that is parallel to one side of the square, but does not pass through Point P:
The image indicates the cross section that is the result of a slice through the pyramid that is perpendicular to the base, parallel to one side of the base, and not passing through the top vertex P, resulting in a cross section that is the shape of a trapezoid. Incorrect Response: D. This response may be the result of the misconception that slicing through a square pyramid in a particular way will result in a distortion of the base resulting in a rectangle. Less common cross sections for a square pyramid can create variations of trapezoids (as shown in the rationale for Incorrect Response B) but not rectangles. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | B |
Objective 008 Correct Response: B. It follows from the diagram that the length of the diagonal for the square is 8 inches. Applying properties of special right triangles to a triangular half of the square (in a 45 degree 45 degree 90 degree triangle, the ratio of the legs to the hypotenuse is 1 to 1 to the square root of 2 ), the side length of the square must be 8 divided by the square root of 2 equals 8 divided by the square root of 2 times the square root of 2 divided by the square root of 2 which equals 8 radical 2 divided by 2 which equals 4 radical 2 inches. This implies that the area of the square is 4 radical 2 the quantity squared is equal to 16 times 2 or 32 square inches. Since the circle has a radius of 4 inches, the area of the circle can be approximated as follows, approximating pie as a value just slightly greater than 3: Pie times r squared equals pi times 4 squared which equals 16 pie or approximately 50 square inches. The area of the shaded region is the difference between these two values: 50 minus 32 = 18 square inches. Incorrect Response: A. This response may be the result of the calculation 8 pie minus 16 in which the area of the square was interpreted to be 16, and it was subtracted from the circumference of the circle. Incorrect Response: C. This response may be the result of the calculation 16 pie minus 16 radical 2 in which the perimeter of the square was subtracted from the area of the circle. Incorrect Response: D. This response may be the result of the calculation , 16 pie minus 32 in which a side length of the square was interpreted to be 8 inches, and the perimeter was used instead of the area. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | B |
Objective 008 Correct Response: B. The length of cable needed on one side of the tree can be calculated by using the Pythagorean Theorem with side lengths 6, (8 minus 2), and 8: A squared plus b squared equals c squared implies the square root of the quantity 6 squared plus 8 squared equals c which implies the square root of 100 equals c which implies c equals 10 feet. Since an additional 1.5 feet of cable is needed for each side, the total length of cable needed for one side of the tree is 11.5 feet Doubling this value produces the correct response, 23 feet. Incorrect Response: A. This response may be the result of calculating the length of 10 feet, then doubling the value without regard for the additional cable needed on each side. Incorrect Response: C. This response may be the result of tripling the value of 8 feet in the problem without regard for the information about the additional cable. Incorrect Response: D. This response may be the result of adding the leg lengths for the triangles on both sides of the tree, then adding 3 for the additional cable: 2 times the quantity 8 plus 6 + 3 = 28 + 3 = 31. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | C |
Objective 008 Correct Response: C. Applying the Pythagorean Theorem with a perpendicular line from the center of the base to the vertex yields the slant height of the pyramid: 30 squared plus 40 squared equals x squared implies x equals the square root of the quantity 30 squared plus 40 squared which implies x equals the square root of 2,500 which implies x equals 50 feet The area of one triangular face of the pyramid is 1 half b times h equals 1 half 60 times 50 which equals 1,500 square feet. Since there are 4 congruent triangular faces, the area of all triangular faces is 4 times 1,500 = 6,000 square feet. Incorrect Response: A. This response represents the area of a single triangular face of the pyramid. Incorrect Response: B. This response may be the result of interpreting the slant height to be equal to the overall height of the pyramid: 4 times the quantity 1 half times 40 times 60 equals 4,800 Incorrect Response: D. This response represents the overall surface area of the pyramid 6,000 for the four triangular faces plus 3,600 for the square base). |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | A |
Objective 009 Correct Response: A. To create an isosceles triangle with A B as the base, point C must be placed such that it is equidistant from A and B. That is, A C and A B must have the same length. Since the point (3, 1) is the midpoint of A B placing a point anywhere along the vertical line x = 3 will ensure that both the vertical and horizontal distance is equal for A C and CB, which will result in congruent side lengths for the segments. Incorrect Response: B. This response may be the result of finding the midpoint between 0 and 8. Incorrect Response: C. This is a possibility but not a necessary condition. Incorrect Response: D. This is a possibility but not a necessary condition. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | B |
Objective 009 Correct Response: B. The definition of a trapezoid is a quadrilateral with at least one set of parallel sides. This figure meets that condition since A B is parallel to D C Incorrect Response: A. Since A B C D is a quadrilateral with at least one pair of opposite sides parallel ( A B is parallel to D C ), it meets the criteria for a trapezoid. Incorrect Response: C. The shape is a trapezoid, but this response incorrectly relates the sides in the figure. A D is not parallel to B C since they have different slopes. Incorrect Response: D. While one pair of opposite sides is parallel ( A B is parallel to D C ), this is not true for A D and B C since they have different slopes. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | A |
Objective 009 Correct Response: A. The length of segment X Y is 7 (found by counting horizontal units). The length of segment XY and Y Z can be found using the distance formula: Incorrect Response: B. This response may be the result of a miscalculation using the distance formula which resulted in same length sides XY and Y Z . Incorrect Response: C. This response may be the result of the misconception that the length of Y Z is equal to the sum differences in the x and y values: 3 + 4 = 7. Incorrect Response: D. This may be the result of using a visual assessment to determine that the side lengths are equal. The calculated values are all distinct. (See the rationale for Correct Response A.) |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | D |
Objective 009 Correct Response: D. Consider the diagram below:
The image from the stem is shown with labels for all interior angles in the diagram. The two base angles in the isosceles triangle are 5 and 6, the third interior angle for the isosceles triangle is 4, the vertical angle to 4 is 1, the angle opposite the 130-degree angle is 2, and the final interior angle in the parallelogram is 3. Since the 130 degree angle is one angle in a parallelogram, we can deduce that the opposite angle, angle 2 is also equal to 130 degrees The sum of the interior angles in a parallelogram is 360 degrees and opposite angles in a parallelogram are congruent, so both angle 1 and angle 3 are equal to . 1 half the quantity 360 minus 2 times 130 equals 1 half times 100 equals 50 degrees. Since angle 1 and angle 4 are vertical angles, the measure of angle 4 is also equal to 50 degrees The triangle in the image is isosceles, where angle 5 and angle 6 are the base angles of the triangle. This means that they both have the same measure, which is 1 half the quantity 180 minus 50 equals 65 degrees.
The image from the stem is shown with measures for all interior angles in the diagram. The two base angles in the isosceles triangle are 65 degrees, the third interior angle for the isosceles triangle is 50 degrees, the vertical angle is 50 degrees, the angle opposite the 130-degree angle is also 130 degrees, and the final interior angle in the parallelogram is 50 degrees. Incorrect Response: A. This response represents the measure of angles 1 and 4 in the diagram, shown in the rationale for Correct Response D, not angle Q. Incorrect Response: B. Consider the diagram shown in the rationale for Correct Response D. This response cannot be true since the measure of angle 4 must be 50 degrees the measure of angles 5 and 6 must be equal, and the sum of the measures of angles 4, 5, and 6 must be 180 degrees Incorrect Response: C. This response may be the result of misinterpreting the triangle in the image to be an equilateral triangle. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | B |
Objective 009 Correct Response: B. The midpoint of segment A B is equidistant from both points. To find it, we can average the x and y values for the coordinates Negative 4, 4 and 8, negative 2 : . Half of negative 4 plus 8, half of 4 plus negative 2 implies 4 halves, 2 halves implies 2, 1 Incorrect Response: A. A point is only equidistant from A and B if it is a point on the perpendicular bisector of A B The slope of A B is A B is y 2 minus y 1 divided by x 2 minus x 1 equals 4 minus negative 2 divided by negative 4 minus 8 equals 6 divided by negative 12 equals negative 1 half. and the midpoint is (2, 1). (See the reasoning provided in the rationale for Correct Response B). The equation for the perpendicular bisector for A B must have a slope of 2 (the opposite reciprocal of Negative 1 half ) and pass through the point (2, 1). Substituting this information into a linear equation in slope-intercept form yields the equation of the perpendicular bisector: Y equals 2 x plus b implies 1 equals 2 times 2 plus b implies b equals negative 3 implies y equals 2 x minus 3 This response is not correct because it is not a point on the line—that is, the x and y coordinates do not satisfy the linear equation: 1 is not equal to 2 times 1 minus 3 Incorrect Response: C. This response is not correct because it is not a point on the perpendicular bisector of A B (see the rationale for Incorrect Response A)—that is, the x and y coordinates do not satisfy the linear equation: Negative 1 is not equal to 2 times 4 minus 3 Incorrect Response: D. This response is not correct because it is not a point on the perpendicular bisector of A B (see the rationale for Incorrect Response A)—that is, the x and y coordinates do not satisfy the linear equation: 4 is not equal to 2 times 8 minus 3 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | B |
Objective 009 Correct Response: B. Consider the following image, which shows triangle A B C after a 90-degree rotation clockwise about the origin.
The image shows a clockwise rotation of triangle A B C about the origin, followed by a translation that moves triangle A B C into the same position as triangle A prime B prime C prime. Note that the location of the rotated image (gray) is close to correct, as is the orientation. A translation (or slide) will move the triangle into the correct location. Incorrect Response: A. This set of transformations places Triangle A B C in the following location:
This image shows a counterclockwise rotation of triangle A B C about point A followed by a reflection over the y axis. Incorrect Response: C. See the rationale shown for Correct Response B to verify that a rotation is necessary at some point to orient the triangle in the correct position. Incorrect Response: D. See the rationale shown for Correct Response B to verify that a rotation is necessary at some point to orient the triangle in the correct position. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | A |
Objective 009 Correct Response: A. Consider the following diagram, which labels three angles that can be used to determine the measure of angle n:
The image from the stem is labeled such that the triangle formed between line a, line c, and line d has interior angle labels 1, 2, and 3. 1 is a vertical angle to the 57 degree angle. 2 is supplementary to the 127 degree angle, and 3 is supplementary to n. Angle 1 represents the vertical angle that is opposite the 57 degree angle, so its measure is also 57 degrees. Angle 2 must be supplementary with the 127 degree angle since they are a linear pair, which means the measure of angle 2 is (180 minus 127) = 53 degrees. Angles 1, 2, and 3 form the interior angles of a triangle, so the sum of their measures must equal 180 degrees, which implies the measure of angle 3 is equal to 180 minus 57 minus 53 = 70 degrees. Finally, angle n must be supplementary to angle 3 since they form a linear pair. This means the measure of angle n is equal to 180 minus 70 = 110 degrees. Incorrect Response: B. This response may stem from the misconception that angle n is twice the measure of the angle labeled 57 degrees. Incorrect Response: C. This is the measure of an angle that is supplementary to 57 degrees, but it is not equal to the measure of angle n. (See the rationale for Correct Response A.) Incorrect Response: D. This response may be the result of thinking that angle n is congruent to the angle labeled 127 degrees, which is not the case. (See the rationale for Correct Response A.) |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | C |
Objective 009 Correct Response: C. Two triangles are similar if two of their corresponding angles are congruent. One pair of congruent angles is given in this response and the other comes from both triangles having right angles (because all right angles are congruent). Incorrect Response: A. One corresponding angle and one congruent corresponding leg is not enough information to establish similarity. Consider the counterexample shown:
Incorrect Response: B. This information is insufficient to establish similarity. As a counterexample, consider a 30 degree 60 degree 90 degree triangle and a 45 degree 45 degree 90 degree triangle. These satisfy the condition (the sums of the non-right angles are equal), but they are not similar. Incorrect Response: D. This information is insufficient to establish similarity. As a counterexample, consider a 30 degree 60 degree 90 degree triangle and a 45 degree 45 degree 90 degree triangle. It is possible that these triangles have the same hypotenuse length but are not similar. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | C |
Objective 009 Correct Response: C. Quadrilateral A B C D is shown in the coordinate plane below:
Quadrilateral A B C D is shown graphed using the coordinates from the question. A horizontal line segment connects the vertices A and C. To find the area, consider a horizontal line connecting points A and C and calculate the area of each triangle separately. The area of the upper triangle is 1 half times 10 times 5 = 25 and the area of the lower triangle is 1 half times 10 times 4 = 20, so the total area of the shape is 45 square units. Incorrect Response: A. This response may be the result of applying the same logic as what is shown in the rationale for Correct Response C but interpreting the value of the base for each triangle to be 6: The absolute value of negative 8 plus 2 equals 6 Incorrect Response: B. This response may be the result of finding the product of the lengths of A B and B C after using the distance formula: 2 radical 13 times 4 radical 2 equals 8 radical 26 This is only valid if the quadrilateral is a rectangle. Incorrect Response: D. This response may be the result of finding the product of the lengths of A B and A D after using the distance formula: Radical 61 times 4 radical 2 equals 4 radical 122 This is only valid if the quadrilateral is a rectangle. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | C |
Objective 009 Correct Response: C. Consider the graph shown.
The graph shows a reflection of the original triangle over the line y = x, followed by a reflection over the line x = 1. The final location of A after those transformations is negative 4, 4. Reflecting point A (4, 2) across the line y = x creates the point , A prime located at (2, 4). (Note that this transformation can also be performed algebraically by transposing the x and y coordinates in the original point A.) The second transformation is a reflection across the line x = negative 1, which transforms point A prime to point A double prime located at negative 4, 4 (This can also be performed algebraically by considering the horizontal distance point A prime is away from the line of reflection.) Incorrect Response: A. This response may be the result of reflecting point A over the x-axis, and then reflecting the point over the line x = negative 1. Incorrect Response: B. This response represents the final location of a different vertex for the original triangle (the vertex initially located at 6 0 Incorrect Response: D. This response represents the location of point A after a reflection across the line y = x and a reflection across the x-axis. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | B |
Objective 010 Correct Response: B. The prefix "deci" refers to "tenth," so there are 10 decimeters in a meter. 18 decimeters is equal to 1.8 meters, which is equivalent to approximately 6 feet. Incorrect Response: A. This response is the result of a misconception about the prefix "centi." There are 100 centimeters in one meter. (18 centimeters is equivalent to approximately 7 inches.) Incorrect Response: C. This response is the result of misconceptions related to the length of a meter. One meter is approximately 3.2 feet, so 18 meters is approximately 58 feet. Incorrect Response: D. This response is the result of a misconception about the prefix "kilo." There are 1000 meters in a kilometer. 18 kilometers is 1,800 meters or approximately 5,900 feet. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | B |
Objective 010 Correct Response: B. The total cost for the lunch order is equal to 42 dollars and 75 cents The change due for a 50 dollars bill is 50 minus 42.75 = 7.25. The fewest number of bills that can be used is 3: 2 one-dollar bills and 1 five-dollar bill. Incorrect Response: A. This response may be the result of misinterpreting the lunch order calculation, specifically misinterpreting the cost of the drinks to be 4 times 2 dollars and 50 cents or 10 dollars and the cost of the 3 sandwiches as 19 dollars This would result in a total cost of , 44 dollars which implies 6 dollars of change. This can be accomplished with 2 bills. Incorrect Response: C. This response may be the result of using the correct computation for the lunch order but misinterpreting the question. If the question asked for the fewest number of bills and coins needed to make the change, the answer would be 4. Incorrect Response: D. This response may be the result of a correct computation of the lunch order but the misinterpretation that the change must be made in one-dollar bills. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | A |
Objective 010 Correct Response: A. The relationship between degrees Fahrenheit and degrees Celsius is C equals 5 ninths times the quantity f minus 32 When F = 98.6, C equals 5 ninths times the quantity 98.6 minus 32 which equals 5 ninths times 66.6 For the purposes of estimation, we can round 66.6 to the nearest multiple of 9, 63, to get
5 ninths times 63 is equal to 5 ninths (9 in the denominator is crossed out) times 9 times 7 over 1 (9 in the numerator is crossed out) equals 5 times 7 or 35 degrees Celsius. Incorrect Response: B. This response may be the result of using an incorrect formula C equals 5 ninths times the quantity f plus 32 to find the temperature in degrees Celsius. Incorrect Response: C. This response may be the result of using an incorrect formula C equals 5 ninths times the quantity f minus 32 to find the temperature in degrees Celsius. Incorrect Response: D. This response may be the result of using an incorrect formula C equals 5 ninths times the quantity f plus 32 to find the temperature in degrees Celsius. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | D |
Objective 010 Correct Response: D. The ratio Width divided by height for the model and the actual building will be equal since the model is to scale. This means that the proportion 6 divided by 12 equals 45 divided by h can be used to calculate the height of the building: 6 divided by 12 equals 45 divided by h implies 6 h equals 540 implies h equals 90 Incorrect Response: A. This proportion does not describe an accurate relationship between the dimensions of the model and the dimensions of the building. This proportion results in an answer of 22.5 feet for the height of the building. Incorrect Response: B. This proportion does not describe an accurate relationship between the dimensions of the model and the dimensions of the building. This proportion results in an answer of 22.5 feet for the height of the building. Incorrect Response: C. This proportion does not describe an accurate relationship between the dimensions of the model and the dimensions of the building. This proportion results in an answer of 1.6 feet for the height of the building. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | B |
Objective 010 Correct Response: B. The figure is composed of two similar triangles. The triangles are similar because their corresponding angles are congruent (i.e., the bottom angle is common to both triangles and the left and right edges are transversals that form 2 pairs of congruent corresponding angles where they intersect the parallel lines). To find y, we can use the following proportion: 9 divided by 12 equals 12 divided by 12 plus y implies 144 equals 9 times the quantity 12 plus y implies 144 equals 108 plus 9 y implies 36 equals 9 y implies y equals 4. To find x, we can use the proportion 9 divided by x is equal to 12 divided by 8 implies 12 x equals 72 implies x equals 6. The ratio of x to y is 6 to 4 or 3 to 2. Incorrect Response: A. This response may be the result of using an incorrect proportion or misinterpreting the value of y to be equal to 3. Incorrect Response: C. This response may be the result of analyzing the ratio 12 to y, which gives 12 to 4 or 3 to 1. Incorrect Response: D. This response may be the result of analyzing the ratio of 12 to 9, which is equal to 4 to 5. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | D |
Objective 010 Correct Response: D. The lines intersect to form the right triangle shown:
The image shows the triangular area that is bounded by the lines in the question. The triangle has a base of 6 units and a height of 6 units. The triangle has a width of 6 units and a height of 6 units, so the area is equal to One half times 6 times 6 equals 18 square units. Incorrect Response: A. This response may be the result of incorrectly interpreting the graph of the lines, or by using the coefficient in the calculation for the area of a triangle. Incorrect Response: B. This may be the result of misinterpreting the dimensions of the triangle to be 3 units tall and 7 units wide. Incorrect Response: C. This may be the result of misinterpreting the dimensions of the triangle to be 3 units tall and 9 units wide. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | B |
Objective 010 Correct Response: B. Consider a triangle with base, b, and height, h. The area of this triangle is equal to . 1 half base times height Doubling the base and the height affects the expression for area as follows: One half times 2 b times 2 h equals 2 b h This expression is equal to 4 times 1 half base times height so doubling both dimensions causes the area to increase by a factor of 4. Incorrect Response: A. This response may be the result of misinterpreting the value 2b2h to mean the area of the original triangle has doubled. Incorrect Response: C. Consider the following counterexample: An isosceles triangle has a base of 6 units and a height of 4 units. The length of the two congruent sides can be found by drawing a perpendicular line from the vertex to the midpoint of the base and using the Pythagorean Theorem to get The square root of 3 squared plus 4 squared equals the square root of 25 equals 5 The perimeter of the triangle is 6 + 5 + 5 = 16 units. Doubling the base and height means the new base is 12 units long, but each of the congruent sides must be equal to The square root of 6 squared plus 8 squared is equal to the square root of 100 which is equal to 10. The new perimeter is now 12 + 10 + 10 = 32 units. This process can be generalized to show that the perimeter doubles when both dimensions are doubled. Incorrect Response: D. Consider the following counterexample: An isosceles triangle has a base of 6 units and a height of 4 units. The length of the two congruent sides can be found by drawing a perpendicular line from the vertex to the midpoint of the base and using the Pythagorean Theorem to get The square root of 3 squared plus 4 squared equals the square root of 25 equals 5 The perimeter of the triangle is 6 + 5 + 5 = 16 units. Doubling the base and height means the new base is 12 units long, but each of the congruent sides must be equal to The square root of 6 squared plus 8 squared is equal to the square root of 100 which is equal to 10. The new perimeter is now 12 + 10 + 10 = 32 units. This process can be generalized to show that the perimeter doubles when both dimensions are doubled. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | C |
Objective 011 Correct Response: C. The sample space represents all possible outcomes for the contest. There are 6 possible outcomes for a winner from two participants A and B choosing one of three difference gifts: {(A, book), (A, gift certificate), (A, smartphone), (B, book), (B, gift certificate), (B, smartphone)}. The number of outcomes in the sample space is equal to the number of people (2) times the number of prizes (3). Incorrect Response: A. In this context, only one person wins, and that winner then makes a choice of which gift to take. The number 3 does not represent the total number of outcomes. Incorrect Response: B. The sum of the number of people and the number of prizes is 2 + 3 = 5, which does not represent the total number of possible outcomes for the contest. (See the reasoning in the rationale for Correct Response C.) Incorrect Response: D. This response indicates that there are 2 cubed = 8 possible outcomes, but there are only 6 unique outcomes for the contest. (See the reasoning in the rationale for Correct Response C.) |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | C |
Objective 011 Correct Response: C. The radius of the large circle is 4, which means the area of the large circle is equal to Pie times r squared equals pie times 4 squared equals 16 pie square units, and the radius of the small circle is 2, which means the area of the small circle is equal to Pie times r squared equals pie times 2 squared equals 4 pie square units. The shaded area represents one quarter of the outer ring, which represents the difference between the area of the large circle and the area of the small circle: 1 fourth times the quantity 16 pie minus 4 pie equals 1 fourth 12 pie which equals 3 pie This shaded region accounts for 3 pie divided by 16 pie equals 3 divided by 16 of the total circular region. Incorrect Response: A. This response represents the area of the shaded region shown.
The image from the question is shown, with a shaded region indicating the area of the small circle only between the radii The area of this shaded region is 1 fourth of 4 pie equals pie, and it represents Pie divided by 16 equals 1 sixteenth of the total circular region. Incorrect Response: B. This response may be the result of interpreting the shaded area to be twice as much as the area shown in the rationale for Incorrect Response A. This would result in a conclusion that the shaded region represents 2 Pie divided by 16 equals 2 sixteenths of the circular area. Incorrect Response: D. This response represents the probability that a beanbag lands in the shaded region shown.
The image from the question is shown with a shaded region that indicates the total area of the diagram (including the small and large circle) between the radii. The shaded area is 1 fourth 16 pie equals 4 pie, and it represents one fourth of the total area for the circular region. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | A |
Objective 011 Correct Response: A. There are 4 prime numbers in each hat: 2, 3, 5, and 7. The total number of possible combinations where both numbers are prime is 4 times 4 = 16. There are 10 times 10 or 100 possible combinations for drawing numbered slips from the hats, so the theoretical probability that two slips are both prime is equal to . 16 hundredths In the experiment, drawing two prime numbers occurred 20 times out of 100, which is 4 more pairs than what we would expect using theoretical probability. Incorrect Response: B. This is most likely the result of the misconception that 1 is a prime number, which would lead to a theoretical probability of . 25 hundredths Incorrect Response: C. This is the result of the misconception that only 3 of the numbers in each hat are prime, which leads to a theoretical probability of . 9 hundredths Incorrect Response: D. This could be the result of reasoning that because 4 out of the 10 numbers in each hat are prime, the probability of drawing two prime numbers is 40 percent or . 40 hundredths (This is equal to the theoretical probability for drawing a single prime number from one hat.) |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | A |
Objective 011 Correct Response: A. Since the letters e and a must be placed consecutively, we can think of e a as a single character within the context of the problem. This means that there are 4 unique characters to use to create a word. The number of possibilities for this is equal to 4 factorial equals 4 times 3 times 2 times 1 equals 24 The stem asks for how many additional arrangements can be formed (excluding "heart"), so the answer is 23. Incorrect Response: B. This response includes the word "heart," which is excluded in the question by "how many additional arrangements ." dot dot dot Incorrect Response: C. This is the result of using the incorrect expression 5 factorial, or 5 times 4 times 3 times 2 times 1 and then subtracting 1 to compensate for the word "heart" since the stem specifies "How many additional arrangements dot dot dot ": 120 minus 1 = 119. Incorrect Response: D. This is the result of the incorrect expression 5 factorial, or 5 times 4 times 3 times 2 times 1 which is most likely the result of considering e and a to be separate characters when calculating the different word arrangements: 5 factorial equals 120 |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | C |
Objective 011 Correct Response: C. The expression 6 factorial equals 6 times 5 times 4 times 3 times 2 times 1 equals 720 can be used to find the number of different arrangements possible for the letters in the word "Boston." However, this counting technique is only the solution if each letter in the word is unique. Since there are two of the letter "o" and swapping the two letters produces the same word, the value of 720 must be halved to compensate for the duplicates: 720 divided by 2 = 360. Incorrect Response: A. This response may be the result of misinterpreting the value of 6 factorial to be equal to the sum of the whole numbers from 6 to 1, rather than the product: 6 + 5 + 4 + 3 + 2 + 1 = 21. Incorrect Response: B. This response may be the result of using the expression . 6 factorial divided by 6 (The denominator in this expression is incorrect for the reasons described in the rationale for Correct Response C.) Incorrect Response: D. This response does not take into consideration the fact that swapping two of the same letter produces the same word rather than a unique arrangement. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | B |
Objective 011 Correct Response: B. Treat the selection of the 2 particular people as one possible outcome and compare it to the total number of ways that any 2 of 10 people may be paired together (i.e., the number of ways to choose 2 of 10 people when the order of their selection does not matter). There are 5 ways to choose the first person and 4 ways to choose the second person, so there are 5 times 4 = 20 ways in which two people may be chosen when the order of their selection matters. However, each pair may have been chosen in 2 different orders, so the total number of pairings is actually 20 divided by 2 = 10. Therefore, the probability is 1 tenth or 10%. Incorrect Response: A. This response may be the result of interpreting the number of possible two-person groupings as 5 times 4 (without dividing by two to account for different combinations of the same two employees). Incorrect Response: C. This response may be the result of assuming there are two unique outcomes in which employees can work together. Since order does not matter, different combinations of the same two employees must all be considered the same outcome. Incorrect Response: D. This response may be the result of using the ratio 2 fifths to calculate the probability. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | C |
Objective 012 Correct Response: C. The left edge of the box in the box plot represents the first quartile of the data set. The first quartile is the median of the lower half of the data. This means that 75 percent of the data in the set are greater than 68. Incorrect Response: A. The median of the data set, represented by the middle bar in the box for the box plot, is 77. The mean test score cannot be deduced from the information shown. Incorrect Response: B. This response may be the result of misinterpreting the relationship between the number line and the box plot. The median of the data set is 77, which is represented by the middle line in the box for the box plot. Incorrect Response: D. Since 68 is the first quartile of the data set, 25 percent of the data fall between 45 and 68. 77 is the median of the data set, which means that 50 percent of the data fall between 77 and the maximum value, 100. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | C |
Objective 012 Correct Response: C. The average amount of tips, in dollars, for the 4 days worked is equal to The sum 34 plus 40 plus 56 plus 82 all divided by 4 equals 212 divided by 4 which equals 53 The equation The sum 34 plus 40 plus 56 plus 82 plus x all divided by 5 equals 58 can be used to find the amount of tips needed on Saturday to make the average 5 dollars greater than the 4-day average. Solving this equation for x leads to: The sum of 212 plus x divided by 5 equals 58 implies 212 plus x equals 290 which implies x equals 78. Incorrect Response: A. This response is the average amount of tips for the four days that are provided: The sum 34 plus 40 plus 56 plus 82 all divided by 4 equals 212 divided by 4 which equals 53 Incorrect Response: B. This response is the average described in the question ( 5 dollars greater than the 4-day average of 53 dollars ), but it does not represent the amount of tips that must be earned on Saturday to achieve this. Incorrect Response: D. This response is 5 dollars greater than the amount of tips earned on Friday. It does not represent the amount needed on Saturday to increase the average in the way specified in the question. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | D |
Objective 012 Correct Response: D. Since this sample only includes respondents with an e-mail address, or respondents who regularly check their e-mail, it may not be a representative sample of the population. The data from this survey could be skewed by the sample of respondents (sampling bias). Incorrect Response: A. Including specific examples does not inherently affect the validity of the conclusion. The question includes an "e.g. list," which provides some specific examples but implies that there are more recreational uses for computers and cell phones than what is provided. Incorrect Response: B. This statement is only true if the sample is biased for some reason. A random sample can be used to make valid conclusions about the population. Incorrect Response: C. While the devices listed are not exhaustive, the conclusion is about the use of a cell phone or computer only. The conclusion does not make claims about use of recreational electronic devices beyond the scope of computer or cell phone use. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | A |
Objective 012 Correct Response: A. A scatter plot is an effective way to analyze two variables and determine correlation. For instance, in this context, it may be the case that the number of absences is negatively correlated with performance on standardized tests (as the number of absences increases, standardized test scores decrease). Incorrect Response: B. Since this type of data is referencing parts (different ages of students) of a whole (students in a primary school) a circle graph would be most appropriate. Incorrect Response: C. A line graph is most appropriate for tracking how one value changes over time (in this case, height). Incorrect Response: D. A double bar graph is appropriate for comparing measures from two distinct sets. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 99 | B |
Objective 012 Correct Response: B. The value 145 is greater than 6 of the values in the data set, which contains a total of 11 values. This means that a height of 145 corresponds to the 55th percentile: 6 elevenths times 100 is approximately 0.55 Incorrect Response: A. This response represents the percent of students with a height greater than 145: 4 elevenths times 100 is approximately 0.36 Incorrect Response: C. This response is the product of 1 eleventh times 7 (the number of values in the data set that are less than or equal to 145): 7 elevenths times 100 is approximately 0.64 Incorrect Response: D. This response may be the result of interpreting the percentile using the fraction 7 tenths (using the number of values less than or equal to 145 and mistaking the number of values in the set to be 10). |
|||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | C |
Objective 012 Correct Response: C. This statement involves the use of interpolation, and the values referenced are consistent with the trend in the scatter plot. This claim is a valid prediction that does not extend beyond the scope of the scatter plot. Incorrect Response: A. This statement is too broad a generalization given the data provided. Incorrect Response: B. A scatter plot allows for analysis of correlation between two variables. The data shown do not provide evidence for claims regarding different variables (factors). Incorrect Response: D. A scatter plot allows for analysis of correlation between two variables. Additional evidence is needed to establish a causal relationship. |
|||||||||||||||||||||||||||||||||||||||||||||||||
| Total Correct: | Review your results against the test objectives. | ||||||||||||||||||||||||||||||||||||||||||||||||||
Open Responses, Sample Responses, and Analyses
| Question Number |
Your Response Read about how your responses are scored and how to evaluate your practice responses |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 101 |
Open Response Item Assignment #1 For each assignment, you may type your written response on the assigned topic in the box provided. Note: The actual test allows you to handwrite your responses on separate response sheets to be scanned for upload to the test. For this practice test, you may handwrite each response on 1–2 sheets of paper. |
||||||||||
| First Sample Weak Response |
First Sample Weak Response to Open-Response Item Assignment #1 A prerequisite skill needed to do this problem is an understanding of exponents. If the student must find the volume of a cube, then he needs to know the formula V = s cubed Otherwise, the student could not solve the problem. I would first remind the students about multiplication being repeated addition. Then I would write the number 5 being multiplied by itself 9 times. on the board and ask, "How are we going to show this without having to write so much! Is it going to be a bigger or smaller answer than adding that many five’s ?" Then I would explain how this can be written in the "shorthand" of mathematics: 5 to the ninth power I would then give them lots of easier examples to do, like the number 2 being multiplied by itself 3 times. This would be a good activity because the standard says to include exponents. The situation given aligns with the standard. To find volume you do use a formula with variables and exponents and replace s, side, with a number. The given situation is a little harder because the teacher is giving the students a problem where you have the answer and must find the s. |
||||||||||
| First Weak Response Analysis |
Analysis of First Weak Response to Open-Response Item Assignment #1 This is an example of a weak response because it is characterized by the following: Purpose: The response addresses all three parts of the assignment in a partial way. For instance, the first part does identify a prerequisite skill, but the candidate explains its relevance to the Situation rather than to the Standard. The second section then describes an activity that shows students what exponents represent, which does not align with the Standard's focus on expressions containing variables. In the third section, the candidate offers an erroneous assessment of the Situation's alignment with the Standard. Subject Matter Knowledge: The response reflects a limited understanding of the subject matter. The candidate misunderstands part one of the assignment when they identify a prerequisite skill for the Situation rather than the Standard. The activity described in part two demonstrates partial understanding of the Standard and limited knowledge of how to enhance students' understanding of the concepts it outlines. While the Standard does mention exponents, the candidate's activity fails to address the Standard's focus on writing and evaluating expressions that contain variables. In part three, the candidate does not realize that the Situation is beyond the scope of the Standard, which includes evaluation of expressions at specific values of their variables (replacing s with a number and finding the volume) but does not include the reverse (being given the volume and finding the value of s). Support: The candidate provides limited supporting evidence. For example, the activity is not described in enough detail to demonstrate how it might enhance students' understanding of the Standard, as the candidate identifies only a superficial connection between this activity and the Standard (that it "says to include exponents"). In addition, the candidate justifies their incorrect assessment of the Situation by identifying a similarly tenuous connection between the Situation and the Standard (the presence of variables and exponents in both). Rationale: The response shows limited reasoning about the topic. For example, the candidate does not explain their choice of prerequisite skill in relation to the Standard. Additionally, the candidate's description of the activity is vague and offers no discussion of how it would enhance students' understanding of this Standard. While the candidate begins to suggest that the Situation is not ideal when they note that this problem would be "harder," they do not realize that it achieves an objective beyond the Standard provided. |
||||||||||
| Second Sample Weak Response |
Second Sample Weak Response to Open-Response Item Assignment #1 A prerequisite skill needed to achieve this standard is the ability to change arithmetic expressions into general expressions by substituting variables for specific numbers. For example, if the total money in pennies earned today is equal to quarters plus dimes plus nickels plus pennies, a general expression could be M = 25q + 10d + 5n + 1p, where M is total money in pennies, q is number of quarters, d is number of dimes, n is number of nickels and p is the number of pennies. Provide students with a sheet of paper with many algebraic expressions and request that they be evaluated with the given values for the variables. For example: a + c + d if a = 3, c = 5 and d = 7 Value is? The situation given does not align with the standard because it is backwards. |
||||||||||
| Second Weak Response Analysis |
Analysis of Second Weak Response to Open-Response Item Assignment #1 This is an example of a weak response because it is characterized by the following: Purpose: The purpose of the assignment is partially achieved. While the candidate identifies a prerequisite skill for the Standard, their explanation is not grade appropriate. Part two outlines a classroom exercise using variables, but the candidate does not discuss how it enhances students’ understanding of the concepts in the Standard. Lastly, the candidate realizes that the Situation does not align with the Standard, but their explanation is unclear. Subject Matter Knowledge: The response shows a limited and at times inappropriate application of subject matter knowledge. When identifying a prerequisite skill, the candidate correctly identifies variables and formulas as key aspects of the Standard, but the example they provide is too advanced to be considered a prerequisite for it (four variables in one expression). In part two, the activity the candidate describes is a series of exercises that does not enhance student understanding of the underlying concepts outlined in the Standard. Finally, while the candidate is accurate in noting that the Situation does not align with the Standard, they do not clearly explain why. Support: The supporting evidence is limited. The prerequisite skill the candidate identifies is appropriate, but the example they choose to illustrate this concept is too advanced for the grade level the assignment indicates (sixth). In the second section, the candidate also outlines passive exercises containing expressions with variables—an activity that lacks student-teacher interaction focusing on skills students need to understand the underlying mathematical concepts. Lastly, while the candidate's assessment of the Situation is correct, they offer only vague support for their conclusion ("it is backwards"). Rationale: The response presents a poorly reasoned discussion of the Standard and how it might be integrated into the classroom. First, the candidate explains their choice of prerequisite skill with an example that goes beyond the scope of the Standard. The activity described is vague, and the candidate does not explain how it would enhance understanding of key concepts covered in the Standard (variables, expressions, formulas). In addition, the candidate offers a limited, very general justification for their assessment of the Situation. |
||||||||||
| First Sample Strong Response |
First Sample Strong Response to Open-Response Item Assignment #1 Prerequisite skill: an understanding of variables. Students must understand that a variable can represent ANY number and change depending on the situation. This leads to the concept of a "rule" or "recipe" to follow in order to solve different situations. These concepts are building blocks for writing formulas and evaluating expressions. Activity: One way to help students understand variables, expressions, and formulas is a game called "What's My Rule?" The teacher draws a table on the board with two rows labeled "input" and "output." She has an equation or "rule" in mind and calls on students to give an input number. She writes the input in the table and the output number below it. This continues until someone can find the rule used to generate the output. The teacher then asks everyone who has found the rule to write it down. Someone gives their rule orally, which is written on the board, and anyone with a different way of describing it shares their way too. Then everyone translates the rule into an expression or formula. Continue the game using rules for different types of expressions that do not contain parentheses. As seen in the sample table, one rule could be "double the input and then add 1." As a formula, it could be written as Output = 2 times Input + 1. This activity supports students' understanding of the standard because they will see expressions as "directions" to follow to get a result. This reinforces that a variable can represent any number and that using variables is a general way to describe a rule. Formulas are an example of "rules" developed to make finding perimeter, area, volume, etc., quick and easy once students understand those concepts and master order of operations. Alignment: The Situation does not align well with this standard. Students can use a formula for the volume of a cube, which contains an exponent. However, the situation works backwards: It provides the "output" and asks students to find the dimensions of the cube, reversing how we normally solve for volume. A more appropriate situation would be for the teacher to ask students to find the volume of a cube when each edge is 5 units.
|
||||||||||
| First Strong Response Analysis |
Analysis of First Strong Response to Open-Response Item Assignment #1 This is an example of a strong response because it is characterized by the following: Purpose: This response addresses all three parts of the assignment in full. The response states a prerequisite skill and explains how it is relevant to the Standard. The candidate also describes an appropriate activity to model the role variables play in formulas/expressions. Lastly, the response identifies that the Situation does not align with the Standard and offers a way to improve it. Subject Matter Knowledge: There is a substantial and accurate application of subject matter knowledge. The response reflects a strong understanding of the Standard (variables and how they are used in expressions). The candidate then describes an age-appropriate activity to enhance students' understanding of expressions/formulas and demonstrate how to translate a rule described in words into an expression containing one variable. Further, the candidate explains how specific components of the game (input, rule) reinforce mathematical concepts (variable, expression) that are fundamental to using formulas to find area, volume, and so forth. Finally, the candidate realizes the Situation given does not align with the Standard and explains why. Support: The candidate provides high-quality, relevant examples to complete all components of the assignment. The prerequisite skill is clearly stated and its relevance explained. The candidate's "What's My Rule?" activity illustrates that "rules" can be expressed mathematically (i.e., as formulas) by using variables to represent any number the student wants to input. The candidate also shares a specific rule that could be used in the game and provides a sample input/output table to simulate one round. Lastly, the candidate reaches a sound conclusion about the Situation, defends why it does not fully align with the Standard, and explains how to revise the Situation for better alignment. Rationale: The response reflects a comprehensive understanding of the topic. The candidate explains how their chosen prerequisite skill is relevant to the standard. The candidate also offers in-depth explanation of how their activity enhances students' understanding of variables, which leads to students writing expressions and therefore lays the groundwork for a future understanding of equations and formulas. The candidate also justifies their assessment of the Situation and explains why their suggested change would better align with the Standard. |
||||||||||
| Second Sample Strong Response |
Second Sample Strong Response to Open-Response Item Assignment #1 1. A prerequisite skill for this standard is an understanding that variables can function as placeholders in evaluating expressions. In elementary school, students were introduced to "placeholders," where shapes stood in for numbers (see example below). The activity below builds upon this concept of placeholder shapes to introduce variables represented by letters. 2. Start the activity with a bag full of green and red circles. Each student takes a handful of circles and places them on their desk. The teacher asks the students to sort their piles into two different rows. Then she asks students to identify the common trait they used to make their two rows. Hopefully they say color! The teacher then explains that every red = 5 points and every green = 10 points. The teacher then asks: How can we make R R R R (or 5 5 5 5) into a shorter expression? They could suggest 4R, 4 times 5, or 4 times 5. Students can then look at the green row (G G G G G) and perform a similar analysis (5G, 5 times 10, or 5 times 10). Now the students must write an expression about their own handful. For example, a student who has 6 red circles plus 4 green circles might write 6R + 4G. Then, they can plug in the values for R and G and evaluate their expression: 6 times 5 + 4 times 10 = 30 + 40 = 70. If each student grabs a new handful, they will notice that the number of green and red circles varies with every turn, while the value of each tile remains constant. The teacher can then ask students to come up with "directions," or a more general expression, for how to find the total points no matter how many of each color are pulled from the bag. Students might say, "multiply the number of red by 5, multiply the number of green by 10, and add them together," or 5R + 10G = total points. 3. The situation does not align with the standard. The situation provides the volume and asks students to find the length of the edge, but this task requires solving an equation, which is not included in the standard. Rather, students should be given the length of one edge of the cube (for example, 6 inches) and asked to find the volume. Example from #1: If delta + 3 = 7, students replaced delta with 4 to solve the equation. Then, students considered what delta + 3 could equal if the value of delta were 5, 8, 10, etc. |
||||||||||
| Second Strong Response Analysis |
Analysis of Second Strong Response to Open-Response Item Assignment #1 This is an example of a strong response because it is characterized by the following: Purpose: The response addresses all three parts of the assignment. The response identifies a prerequisite skill for the Standard and explains how it is relevant. The candidate also describes an activity that builds upon students' prior knowledge to model the concept of variables as placeholders in evaluating expressions. Finally, the candidate identifies that the Situation does not align with the Standard and provides a possible remedy. Subject Matter Knowledge: There is a substantial application of subject matter knowledge. The response reflects a clear and accurate understanding of the Standard (how variables are used as placeholders in evaluating expressions) and demonstrates further understanding of how this Standard builds on curriculum objectives in earlier grades. In the second section, the candidate outlines an activity that both enhances students' understanding of how to evaluate an expression and allows students to practice writing their own expressions based on a real-world situation (their handful of red and green circles). The candidate realizes that the Situation does not align with the standard and explains why. Support: The candidate provides high-quality, relevant support throughout the response. The prerequisite skill is clearly stated, and the candidate explains its relevance to the Standard. The candidate also describes their activity in detail, demonstrating how students will use manipulatives and providing an example to illustrate how a student might engage with a particular combination of circles (4 red and 5 green). Additionally, the candidate explains how the lesson enhances student understanding by connecting specific aspects of the activity (number of circles, directions) with concepts addressed in the Standard (variable, expression). Rationale: The response reflects an ably reasoned, comprehensive understanding of the topic. The candidate explains how students' prerequisite knowledge of variables as placeholders is relevant to the Standard. The candidate then outlines all steps in the activity and provides a thorough explanation of how it enhances students' understanding of variables, generalized expressions, and how their values can change. The candidate justifies their statement that the Situation does not align with the Standard and offers a way to revise it. |
||||||||||
| 102 |
Open-Response Item Assignment #2 For each assignment, you may type your written response on the assigned topic in the box provided. Note: The actual test allows you to handwrite your responses on separate response sheets to be scanned for upload to the test. For this practice test, you may handwrite each response on 1–2 sheets of paper. |
||||||||||
| First Sample Weak Response |
First Sample Weak Response to Open-Response Item Assignment #2 The student is confused about how many inches are in a foot. Half of a foot is not point 6 feet. The student correctly multiplies 4 times 8 and 6 tenths, but 6 tenths is not the correct number to use. It should be 4 times 8 and 1 half The student needs the rules of operations with fractions explained to her again. The correct solution is 6 and 1 half plus 32 and 1 half = 39 feet. To help the student understand that 6 inches is not point 6 feet, I would have her look at a ruler and ask her to find 6 inches on it. I would then ask the student how many inches there are in a foot. You have 6 inches out of 12 inches, which is 6 twelfths Now have the student reduce the fraction to get 1 half By using the ruler, the student can see that 6 inches is really one half of a foot. |
||||||||||
| First Weak Response Analysis |
Analysis of First Weak Response to Open-Response Item Assignment #2 This is an example of a weak response because it is characterized by the following: Purpose: The purpose of the assignment is partially achieved. The first part correctly identifies one of the three errors in the Student Response. In the second part, the candidate does give an answer to the Problem, but it is incorrect and ignores the final step of converting feet into yards. The response then offers an alternative way to help the student understand one of the three errors and explains why it would be helpful. Subject Matter Knowledge: The response shows a limited, at times inaccurate application of subject matter knowledge. One error in the Student Response is correctly identified (that 6 inches is not point 6 of a foot), and the candidate gives an alternative approach to help the student understand that 6 inches equals 1 half foot. However, the candidate fails to recognize the other two errors in the Student Response. In addition, the candidate incorrectly states that the Student Response correctly multiplies 4 times 8 and 6 tenths, demonstrating that they misunderstand how to multiply a whole number by a mixed number. As a result, the candidate's own answer to the Problem is also incorrect. Support: The supporting evidence is limited. For example, although the candidate correctly identifies one of the student's errors, they do not specify what rules the student might need "explained again" or how those rules might correct the error. The candidate also never addresses two other errors that appear in the Student Response. Additionally, because the candidate does not show their work in part two, the reason they arrive at an incorrect answer remains unclear—whether, for instance, the candidate has fundamentally misunderstood the Problem or made a calculation error. Finally, the alternative method only addresses one student error. Rationale: The response shows limited reasoning about the topic. The candidate identifies only one of three errors in the Student Response, and with limited justification. In part two, the candidate does not show their work in enough detail to demonstrate the reasoning that led to their (incorrect) answer. While the candidate does describe a method to address one of the student's misconceptions, they fail to recognize the other errors and ultimately to assist the student in finding the correct answer. |
||||||||||
| Second Sample Weak Response |
Second Sample Weak Response to Open-Response Item Assignment #2 The student does not know how many inches there are in a yard. The student does not know how to multiply mixed fractions. The student does not know how to change feet into yards. The perimeter is 40 feet and 6 inches. First, help the student change 1 half into inches. Then work with this addition problem: 6 feet and 6 inches PLUS 8 feet and 6 inches PLUS 8 feet and 6 inches PLUS 8 feet and 6 inches PLUS 8 feet and 6 inches. Add the whole numbers together to get 38 feet . Then add up the inches getting 30 inches. Remember 12 inches make a foot. Your 30 inches are 2 feet (24 inches) plus 6 inches. The final perimeter answer is 40 feet and 6 inches. Remember one yard is 36 inches or 3 feet . Regroup your feet to make yards, and anything left over becomes a fractional part of a yard. |
||||||||||
| Second Weak Response Analysis |
Analysis of Second Weak Response to Open-Response Item Assignment #2 This is an example of a weak response because it is characterized by the following: Purpose: All three parts of the assignment have been addressed, but in a limited way. In part one, the student's mistakes made are listed but not explained. In part two, the candidate's solution is correct but incomplete (not converted into yards). In part three, the alternative method focuses on finding the correct answer rather than improving the student's conceptual understanding. Subject Matter Knowledge: There is a limited application of subject matter knowledge. In part one, the response lists three errors, but the candidate does not explain those errors in the context of the Student Response or discuss misconceptions that might have led to them. In part two, the solution is partially complete. In part three, the alternative approach does provide a way to answer the Problem, but it does not address the student's misunderstanding of multiplication of mixed numbers by whole numbers. Part three further demonstrates limited knowledge of how to enhance students' conceptual understanding of unit conversion (inches to feet, feet to yards). Support: The supporting evidence is limited. In part one, the candidate does not use specifics from the Student Response to explain the errors they have identified, and they do not consider possible misconceptions that caused the errors. In part two, the solution is correct but incomplete, as the Problem requires a final answer in yards rather than feet. In part three, the candidate does not connect their alternative method with the conceptual errors identified in part one; for instance, this method helps the student to avoid fractions rather than directly addressing their conceptual misunderstandings of fractions and unit conversion. Rationale: The response reflects a poorly reasoned understanding of the topic. In part one, the candidate lists errors without explaining where or why they might have occurred in the Student Response, which further obscures how and why their alternative method might address those errors. In part three, the candidate does not justify their alternative method, as it merely helps the student to find the correct perimeter rather than addressing the misconceptions the Student Response demonstrates. Since the candidate also does not show their reasoning in part two, the response ultimately fails to illustrate the candidate's own knowledge of fractions and multiplication involving mixed numbers. |
||||||||||
| First Sample Strong Response |
First Sample Strong Response to Open-Response Item Assignment #2 1. The student understands that perimeter is the distance around a figure and attempts to add the five sides. The student also recognizes that one of the lengths is different from the others, and that common denominators are needed to add fractions. However, he does not understand that 8 feet 6 inches is the same as 8 and 1 half feet, nor that 4 times 8 and 6 tenths does not equal 32 and 6 tenths The student also incorrectly converts the answer into yards, as he multiplies (rather than divides) the sum by 3.
2. The correct answer is
6 and one half plus 4 times 8 and one half equals 6 and one half plus open paren 4 times 8 plus 4 times one half close paren equals 6 and one half plus 32 plus 2 equals 40 and one half feet 3. The student misunderstands three concepts: the number of inches in 1 foot, multiplication of whole and mixed numbers, and conversion of feet into yards. --Show the student a ruler and have him place a finger on the 6-inch mark. Ask how many pieces his finger cuts the ruler into and whether these pieces are equal. The student will see that the ruler is cut in half at the 6-inch mark, reinforcing the fact that 6 inches equals 6 twelfths feet and 6 twelfths = . one half --Remind the student that 4 times 8 and one half is the addition of 4 groups of 8 and one half, or 8 and one half plus 8 and one half plus 8 and one half plus 8 and one half The student was correct that 4 times 8 is 32, but he did not distribute the 4 to the one half Now he can add the four halves to get 2 for an answer of 32 + 2 = 34, and then add that to the last side, which is 6 and one half feet. 34 + 6 and one half is 40 and one half This emphasizes that multiplication is repeated addition and uses this concept to arrive at the correct product. --Use a yardstick to help the student see that 3 feet make 1 yard. Give the student a 12-foot piece of string and a yardstick. Ask how long the string is in both feet and yards. The student will see that the number of yards is smaller than the number of feet, and since 3 feet = 1 yard, we need to divide (not multiply) the number of feet by 3. Then, have the student consider 40 and one half divided by 3 in two steps. First, 40 divided by 3 is 13 with 1 foot left over. Then this foot can be added to one half foot to get 1 and one half feet. Have the student place his/her finger on 1 and one half feet on the yardstick to illustrate that it is 1 and one half of a yard. |
||||||||||
| First Strong Response Analysis |
Analysis of First Strong Response to Open-Response Item Assignment #2 This is an example of a strong response because it is characterized by the following: Purpose: The purpose of the assignment is fully achieved. The response addresses all three parts of the prompt. The candidate's analysis of the Student Response identifies concepts that the student understands in addition to errors and misconceptions. The candidate also provides the correct solution to the Problem. The response recognizes three conceptual errors in the Student Response and gives an alternative approach to help the student understand each of those concepts. Subject Matter Knowledge: The response shows substantial application of subject matter knowledge. The candidate has found the correct perimeter for the fence. When showing their work to calculate the perimeter, the candidate also demonstrates a strong understanding of multiplication involving fractions, division involving fractions, and conversion of units. The alternative methods included in the response recognize what the student has misunderstood and devises activities that not only aid the student in finding the correct final answer but also strengthen their understanding of the underlying mathematical concepts at each step. Support: The response clearly identifies three errors in the Student Response, explains where they occur, and describes the conceptual misunderstanding that likely caused each one. In addition, the candidate provides a correct solution to the Problem and supports their answer by showing their calculations step by step. Finally, the candidate describes each component of their alternative method in detail, including the use of manipulatives to reinforce mathematical concepts; they also explain how these methods would address the student's misunderstandings of, for example, multiplication of mixed numbers and unit conversion. Rationale: This response shows an ably reasoned understanding of the topic. The student's errors are identified, and the candidate explains the misconceptions that generated those errors. Accurate, step-by-step calculations demonstrate how the candidate arrived at the correct solution to the Problem in part two. Lastly, the response clearly aligns each alternative approach in part three with an error in the Student Response, and the candidate explains how each activity would address each misconception. |
||||||||||
| Second Sample Strong Response |
Second Sample Strong Response to Open-Response Item Assignment #2 The student knows that finding perimeter means adding all 5 sides together. However, the student thinks that 10 inches make one foot (instead of 12 inches), which leads her to the wrong fraction: she changed 6 inches to 6 tenths of a foot instead of 6 twelfths (or one half ). Multiplying 8 and 6 tenths by 4 would have been an appropriate method if 6 tenths were the right fraction. Unfortunately, the student only multiplied 8 by 4 and ignored the fraction. Although these errors lead her to the incorrect perimeter, she did correctly convert the improper fraction to a mixed number. The student also knows that 3 feet makes a yard but multiplied their total feet by 3 instead of dividing by 3. Correct solution: 6 and one half plus 4 times 8 and 6 twelfths equals 6 and one half plus 4 times 8 plus 4 times one half equals 6 and one half plus 32 plus 2 equals 40 and one half feet. Divide 40.5 by 3 equals 13.5 yards or 13 and one half yards The student's first mistake was to make incorrect fractional conversions. Real rulers and a yard stick (or paper models) would provide the student with concrete ways of understanding that half of a foot is 6 inches. Ask the student to count out 6 inches on a ruler; point out that it is in the middle of the ruler and therefore one half of a foot. If you have a paper model, fold it into 2 equal parts to demonstrate. The student also had difficulty multiplying a mixed number by a whole number. Ask the student to break 8 and one half into 8 whole rulers plus a one half ruler. Then multiply 4 by 8, which equals 32, and multiply 4 by one half which equals 2. If necessary, place a 6-inch paper on a ruler four times to show that it makes 2 whole rulers. We now have 6 and one half + 32 + 2, or 40 and one half feet. Lastly, pull out a yard stick. Ask the student to notice that a ruler is smaller than a yard stick and see how many rulers make one yard stick. Then ask the student to physically count out 40 and one half feet on the yardstick, recording every time they make one yardstick (39 feet requires 13 yardsticks) and any remaining part that does not equal a whole yard ( one and one half feet left over). Note how much of a yard this is by counting one and one half feet out on the yardstick. Find that it is 18 inches long, which is half of the 36 inches needed for one yard. If needed, fold a paper model yard stick to show that one and one half feet is in the middle. The student will then get the final answer 13 and one half yards |
||||||||||
| Second Strong Response Analysis |
Analysis of Second Strong Response to Open-Response Item Assignment #2 This is an example of a strong response because it is characterized by the following: Purpose: The purpose of the assignment is fully achieved. In part one, the candidate provides a complete analysis of the three errors in the Student Response in addition to discussing mathematical concepts the student has understood. In part two, the correct solution is provided, and the candidate shows the method they used to find it. In part three, the candidate details an alternative method that addresses the student's major misconceptions and uses visuals to cement the concepts. Subject Matter Knowledge: There is accurate and appropriate application of subject matter. In part one, the candidate identifies the student's misunderstanding of conversions between inches and feet as well as between feet and yards. The candidate further explains the errors the student makes when multiplying a mixed number by a whole number. Part two provides a complete correct solution to the Problem, and it demonstrates the candidate's understanding of concepts such as multiplication of mixed numbers and unit conversion. In part three, the candidate presents an age-appropriate alternative approach that uses physical models to build on the student's prior knowledge. Support: The candidate provides sound supporting evidence in all three parts of the response. In part one, the candidate refers to specifics in the Student Response to clarify the errors identified (for instance, pointing out that the student erroneously converts 6 inches to 6 tenths of a foot). In part two, the candidate's response includes step-by-step calculations to both support their correct answer and demonstrate their knowledge of the concepts and skills needed to solve it. Part three gives a detailed description of the candidate's alternative method, including specifics about their use of manipulatives to enhance students' conceptual understanding. Rationale: This response reflects an ably reasoned understanding of mathematical concepts and how to enhance student understanding of them in the classroom. In part one, the student's misunderstandings are both identified and explained. In part two, the candidate not only finds the correct solution but also breaks the Problem down to show their reasoning at each step. In part three, the candidate develops an age-appropriate remediation technique that explains how to correct the student's conceptual misunderstandings with concrete, real-world examples. |
||||||||||
| Review the Performance Characteristics and Score Scale for Written Performance Assignments. | |||||||||||
Multiple Choice Question
Practice Test Evaluation Chart
In the evaluation chart that follows, the multiple-choice questions are arranged in numerical order and by test objective. Check your responses against the correct responses provided to determine how many questions within each objective you answered correctly.
Subarea 1 : Number Systems and Operations
Objective 0001: Apply number theory, structures of numeration systems, and arithmetic properties to the real number system.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 1 | A | |
| 2 | A | |
| 3 | D | |
| 4 | B | |
| 5 | D | |
| 6 | D | |
| 7 | B | |
| 8 | C | |
| 9 | C | |
| 10 | D | |
| 11 | D |
out of 11
Objective 0002: Demonstrate knowledge of the principles and operations related to whole numbers, decimals, and percents.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 12 | B | |
| 13 | C | |
| 14 | B | |
| 15 | A | |
| 16 | D | |
| 17 | B | |
| 18 | C | |
| 19 | D | |
| 20 | A | |
| 21 | C | |
| 22 | A | |
| 23 | C | |
| 24 | B |
out of 13
Objective 0003: Understand principles and operations related to integers and fractions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 25 | C | |
| 26 | B | |
| 27 | C | |
| 28 | A | |
| 29 | A | |
| 30 | D | |
| 31 | D | |
| 32 | C | |
| 33 | B | |
| 34 | B | |
| 35 | B | |
| 36 | A | |
| 37 | A |
out of 13
Subarea 1 (Objectives 0001–0003) Total out of 37
Subarea 2 : Algebraic Thinking and Relations
Objective 0004: Analyze patterns and the properties of functions and relations.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 38 | D | |
| 39 | D | |
| 40 | A | |
| 41 | C | |
| 42 | D | |
| 43 | B | |
| 44 | C |
out of 7
Objective 0005: Understand how to manipulate and simplify algebraic expressions and translate problems into algebraic expressions, equations, and inequalities.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 45 | C | |
| 46 | B | |
| 47 | D | |
| 48 | C | |
| 49 | A |
out of 5
Objective 0006: Understand properties and applications of ratios and proportions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 50 | D | |
| 51 | B | |
| 52 | C | |
| 53 | D | |
| 54 | D | |
| 55 | B | |
| 56 | A |
out of 7
Objective 0007: Analyze properties and applications of linear relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 57 | A | |
| 58 | A | |
| 59 | C | |
| 60 | D | |
| 61 | B | |
| 62 | B |
out of 6
Subarea 2 (Objectives 0004–0007) Total out of 25
Subarea 3 : Geometry
Objective 0008: Analyze the characteristics and properties of two- and three-dimensional figures.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 63 | B | |
| 64 | C | |
| 65 | A | |
| 66 | B | |
| 67 | B | |
| 68 | C | |
| 69 | B | |
| 70 | B | |
| 71 | C |
out of 9
Objective 0009: Understand the principles and properties of coordinate and transformational geometry.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 72 | A | |
| 73 | B | |
| 74 | A | |
| 75 | D | |
| 76 | B | |
| 77 | B | |
| 78 | A | |
| 79 | C | |
| 80 | C | |
| 81 | C |
out of 10
Subarea 3 (Objectives 0008–0009) Total out of 19
Subarea 4 : Measurement, Data, and Probability
Objective 0010: Understand principles, concepts, and procedures related to measurement.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 82 | B | |
| 83 | B | |
| 84 | A | |
| 85 | D | |
| 86 | B | |
| 87 | D | |
| 88 | B |
out of 7
Objective 0011: Understand the fundamental principles of probability.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 89 | C | |
| 90 | C | |
| 91 | A | |
| 92 | A | |
| 93 | C | |
| 94 | B |
out of 6
Objective 0012: Understand descriptive statistics and the methods used in collecting, organizing, reporting, and analyzing data.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 95 | C | |
| 96 | C | |
| 97 | D | |
| 98 | A | |
| 99 | B | |
| 100 | C |
out of 6
Subarea 4 (Objectives 0010–0012) Total out of 19
Practice Test Score Calculation
The practice test score calculation is provided so that you may better gauge your performance and degree of readiness to take an MTEL test at an operational administration. Although the results of this practice test may be used as one indicator of potential strengths and weaknesses in your knowledge of the content on the official test, it is not possible to predict precisely how you might score on an official MTEL test.
The Sample Responses and Analyses for the open-response items may help you determine whether your responses are more similar to the strong or weak samples. The Scoring Rubric can also assist in estimating a score for your open responses. You may also wish to ask a mentor or teacher to help evaluate your responses to the open-response questions prior to calculating your total estimated score.
How to Calculate Your Practice Test Score
Review the directions in the sample below and then use the blank practice test score calculation worksheet to calculate your estimated score.
Multiple-Choice Section
| Enter the total number of multiple-choice questions you answered correctly: | 66 | ||
| Use Table 1 below to convert that number to the score and write your score in Box A: | A: | 195 |
Open-Response Section
| Enter the number of points (1 to 4) for your first open-response question: | 2 | ||
| Enter the number of points (1 to 4) for your second open-response question: | 3 | ||
| Add those two numbers (Number of open-response question points): | 5 | ||
| Use Table 2 below to convert that number to the score and write your score in Box B: | B: | 46 |
Total Practice Test Score (Estimated MTEL Score)
| Add the numbers in Boxes A and B for an estimate of your MTEL score: | A + B = | 241 |
Practice Test Score Calculation Worksheet: Elementary Mathematics (68)
Table 1:
| Number of Multiple-Choice Questions Correct | Estimated MTEL Score |
|---|---|
| 0 to 25 | 131 |
| 26 to 30 | 138 |
| 31 to 35 | 145 |
| 36 to 40 | 152 |
| 41 to 45 | 160 |
| 46 to 50 | 167 |
| 51 to 55 | 174 |
| 56 to 60 | 181 |
| 61 to 65 | 188 |
| 66 to 70 | 195 |
| 71 to 75 | 202 |
| 76 to 80 | 209 |
| 81 to 85 | 216 |
| 86 to 90 | 223 |
| 91 to 95 | 230 |
| 96 to 100 | 237 |
Table 2:
| Number of Open-Response Question Points | Estimated MTEL Score |
|---|---|
| 2 | 31 |
| 3 | 36 |
| 4 | 41 |
| 5 | 46 |
| 6 | 50 |
| 7 | 55 |
| 8 | 60 |
Use the form below to calculate your estimated practice test score.
Multiple-Choice Section
| Enter the total number of multiple-choice questions you answered correctly: | |||
| Use Table 1 above to convert that number to the score and write your score in Box A: | A: |
Open-Response Section
| Enter the number of points (1 to 4) for your first open-response question: | |||
| Enter the number of points (1 to 4) for your second open-response question: | |||
| Add those two numbers (Number of open-response question points): | |||
| Use Table 2 above to convert that number to the score and write your score in Box B: | B: |
Total Practice Test Score (Estimated MTEL Score)
| Add the numbers in Boxes A and B for an estimate of your MTEL score: | A + B = |

 = 0.05 + 0.20 = 0.25.
= 0.05 + 0.20 = 0.25.
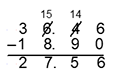
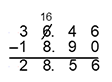
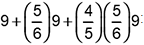
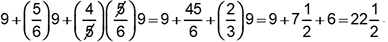
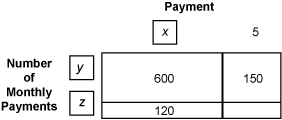
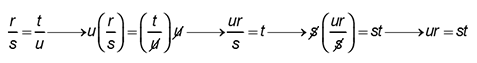

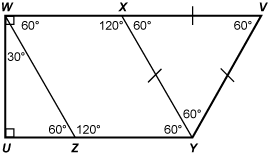


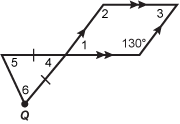
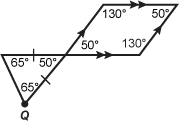



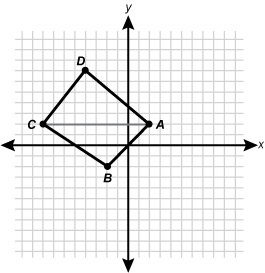
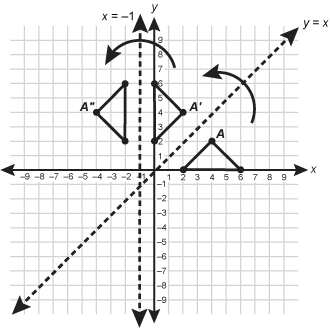
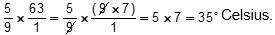
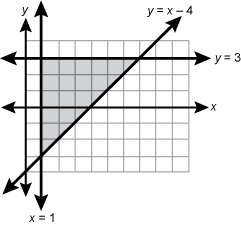
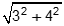 =
=
 =
=