Practice Test: Middle School Mathematics (65)
Answer Key, Sample Responses, Evaluation Chart, and Score Calculation Tool
Answer Key
Fill in your answers below and then print this answer key to save your work. Alternatively, you can print the answer key first to fill it out offline as you take the practice test. Note that the correct responses will be displayed on the printed answer key, so you may want to cover them until you have completed the practice test and are ready to check your answers.
When you have finished the practice test, click on "show answers" to see how well you did on each objective. In addition, use the Evaluation Chart to determine how many questions within each objective you answered correctly.
You will not receive a score for the practice test, and there is no passing score for the practice test. However, to get a sense of how well you did, use the Score Calculation Tool to better gauge your performance and degree of readiness to take an MTEL test at an operational administration.
NOTE: When you take the actual test, you will receive a score report that provides subarea-level performance, not objective-level performance. Information about test results can be found at Score Report Explanation.
| Question Number | Your Response | Correct Response |
Related Objectives and Rationale |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | C |
Objective 001 Correct Response: C. This claim may be verified with simple examples, such as pi to the 0 power equals 1 and radical 2 squared equals 2. Incorrect Response: A. The sum of an irrational number plus a rational number is irrational. Consider that a non-repeating, nonterminating decimal will remain as such when any terminating or repeating decimal is added to it. Incorrect Response: B. The quotient of an irrational number divided by a rational number is irrational. Suppose that A divided by b formed a rational number, m divided by n. Then it would follow that A equals b times the fraction m over n. That is, A would also be a rational number. This result contradicts the statement that A is an irrational number and so it cannot be true. Incorrect Response: D. The sum of an irrational number plus a rational number is irrational. See the rationale for response A. |
|||||||||||||||||
| 2 | B |
Objective 001 Correct Response: B. There are 3 sets of identical groups of x plus 4 shown, or the quantity x plus 4 plus the quantity x plus 4 plus the quantity x plus 4. This may be written as 3 times the quantity x plus 4 by the distributive property of equality. Incorrect Response: A. Since each of the three rods represents x, 3x is the correct term to represent the unknowns in the problem. However, this answer does not distribute the factor of 3 to the ones units shown—there are 12 ones units in the diagram, not 4. Incorrect Response: C. The exponent signifies repeated multiplication of x plus 4. This expression would correspond to the total volume of a cube that has an edge length of x plus 4. This is not what is shown in the diagram. Incorrect Response: D. This response may reflect a misconception that an exponent represents repeated addition (e.g., the multiplication of 4 and 3). The expression 4 cubed denotes 4 times 4 times 4 equals 64 ones units. |
|||||||||||||||||
| 3 | D |
Objective 001 Correct Response: D. Given that K is a multiple of x, then K equals m times x for some whole number m. Similarly, given that K is a factor of y, then Y divided by K equals n for some whole number n. It follows from the substitution of K that Y divided by the product mx equals n implies y equals m times x times n. That is, y is a multiple of x. Incorrect Response: A. Given that K is a factor of y, then Y divided by K equals n for some whole number n. Take the reciprocal of both sides of the equation to see that K divided by y equals 1 divided by n. As such, K divided by y can only be a whole number if K = y. Incorrect Response: B. Given that K is a multiple of x, then K equals m times x for some whole number m. Dividing both sides of this equation by m times x shows that x divided by K equals that unit fraction 1 divided by m: K over the product m times K equals m times x divided by m times k implies 1 over m equals x over k. This means that x divided by k is only a whole number when x = K. Incorrect Response: C. For a proof by counterexample, consider the values K = 4, x = 2, and y = 8. These values are consistent with the information provided. In this case, y is not a factor of x, so the claim that "y is a factor of x" must not always be true. |
|||||||||||||||||
| 4 | B |
Objective 001 Correct Response: B. The prime factorization of 300, 480, and 840 is as follows:
Incorrect Response: A. This response reflects the number of prime factors in the greatest common factor. Incorrect Response: C. This response may be chosen for being the sum of the exponents when 300 is written as a product of its prime factors, 2 squared times 3 times 5 squared. Incorrect Response: D. This response reflects the sum of the greatest exponent associated with each factor common to all three numbers: 2 to the fifth 3 and 5 squared. This may indicate a misconception about the definition of a greatest common factor. |
|||||||||||||||||
| 5 | D |
Objective 001 Correct Response: D. The expanded form of the number represented as "1 Y 3" is equal to 1 times 100 plus Y times 10 plus 3 times 1. Multiplying the digit Y by 24 corresponds to a partial product of 24 times 10 times Y equals 240 times Y. Incorrect Response: A. 20 times Y does not reflect the contribution of the 4. The correct partial product can be written with the distributive property as The quantity 20 plus 4 times 10 times y. Incorrect Response: B. The tens place value is not expressed with 24 times Y. This response treats the digit Y as though it represented Y units of 1. Incorrect Response: C. This response may represent 4 times 10 times Y. This product does not account for the multiplication between Y and the digit 2 in 24. |
|||||||||||||||||
| 6 | D |
Objective 001 Correct Response: D. Division by 2 will distribute over each of the terms in the parentheses: 2 times 6 to the sixth power divided by 2 plus 10 times 6 to the fourth power divided by 2 plus one half times 6 squared divided by 2 equals six to the sixth power plus 5 times six to the fourth power plus one fourth times 6 squared. Incorrect Response: A. This answer is the result of a misapplication of the distributive property in which the base for each exponential expressing is divided by 2. (It does not hold, for instance, that 6 squared times 18 divided by 2 is equal to 3 squared times 9.) Incorrect Response: B. This response demonstrates a misconception with the division of products in which the exponent for each exponential expression is halved. (It does not hold, for instance, that 6 squared divided by 2 is equal to 6.) Incorrect Response: C. The response 6 cubed plus 5 times 6 squared plus one fourth times 6 could be obtained from multiple errors, such as dividing both the constants and the exponents for each expression by 2. |
|||||||||||||||||
| 7 | C |
Objective 001 Correct Response: C. The value of a number does not change if a pair of inverse operations are applied to it. The pair of equations 4 times 8 equals 32 and 32 divided by 8 equals 4 shows division by 8 reversing the effect of multiplication by 8. Incorrect Response: A. In this response, multiplication occurs with one number and division with its integer opposite. This does not demonstrate the concept of inverse operations. The inverse operation of multiplication by 1 is division by 1, not negative 1. However, even if this were addressed, the concept of inverse operations would not be well illustrated by multiplication and then division by 1. Incorrect Response: B. This response demonstrates properties of zero, not inverse operations. Incorrect Response: D. These equations multiply and divide by different numbers, making them inappropriate to use to illustrate the concept that multiplication and division are inverse operations. |
|||||||||||||||||
| 8 | B |
Objective 001 Correct Response: B. The time it takes the light to travel is equal to the distance it travels divided by its speed: 1.5 times 10 to the twelfth plus 1.5 times 10 to the eighth all divided by 3 times 10 to the eighth. Divide the numerator and the denominator by 10 to the eighth power to obtain 1.5 times 10 to the fourth plus 1.5 times 10 to the 0 all divided by 3. The expression can now be written as one third times the quantity 15,000 plus 1.5. Incorrect Response: A. This response is 10 times less than the correct response, which may indicate a misconception that may have arisen because 1.5 shows a decimal and 3 does not or because of an error in dividing by the powers of 10 in the number by 10 to the eighth power. Incorrect Response: C. This response is 10 times greater than the correct response, which may indicate a misconception that may have arisen because 1.5 shows a decimal and 3 does not or because of an error in dividing by the powers of 10 in the number by 10 to the eighth power. Incorrect Response: D. This response is 100 times greater than the correct response. |
|||||||||||||||||
| 9 | C |
Objective 001 Correct Response: C. A power with a negative exponent is equivalent to the reciprocal of that power with a positive exponent. The expression simplifies as 2 to the negative third power times 3 all divided by 3 to the negative second power times 5 squared equals one over 2 cubed times 3 all divided by 1 over 3 squared times 5 squared equals three eighths divided by 25 ninths equals 3 eighths times 9 twenty-fifths equals 27 over 200. Incorrect Response: A. This response could be obtained from evaluating the expression as Negative 6 times 3 divided by negative 6 times 10. This indicates a misunderstanding that exponents signify binary multiplication (e.g., 5 squared = 5 times 2 = 10) and not repeated multiplication (e.g., 5 squared = 5 times 5 = 25). Incorrect Response: B. This response could be obtained by misinterpreting the meaning of negative exponents: Negative 8 times 3 divided by negative 9 times 25. Incorrect Response: D. This response is the result of interpreting 2 to the negative third power times 3 all divided by 3 to the negative second power times 5 squared as 3 times 5 squared all divided by 2 cubed times 3 squared. |
|||||||||||||||||
| 10 | A |
Objective 001 Correct Response: A. In Step 2, the teacher includes tiles representing the additive inverses plus 3 and negative 3 to the original set of plus 3 tiles. This is equivalent to adding 0 to the original value, which is justified by the additive identity property. Incorrect Response: B. The associative property would be demonstrated by showing how 3 separate tiles have the same total sum regardless of whether the middle pile is combined with the left or right pile first. 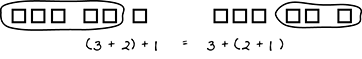 Five blocks are spaced such that three are grouped together. The five blocks are circled, and one block is outside the circle. Beneath the image the expression open parentheses 3 plus 2 closed parentheses plus 1 is shown. This image is shown to be equal to a second image, which depicts 6 blocks total, with three blocks being grouped together. Beneath the second image is the expression 3 plus open parentheses 2 plus 1 closed parentheses.
Five blocks are spaced such that three are grouped together. The five blocks are circled, and one block is outside the circle. Beneath the image the expression open parentheses 3 plus 2 closed parentheses plus 1 is shown. This image is shown to be equal to a second image, which depicts 6 blocks total, with three blocks being grouped together. Beneath the second image is the expression 3 plus open parentheses 2 plus 1 closed parentheses.
Incorrect Response: C. The commutative property would be demonstrated by showing how the sum of 2 separate piles of tiles is not affected by the order in which the groups are combined.  Five blocks are spaced apart in two different configurations to show that 3 plus 2 is the same as 2 plus 3
Five blocks are spaced apart in two different configurations to show that 3 plus 2 is the same as 2 plus 3
Incorrect Response: D. The multiplicative inverse property states that the product of any number and its reciprocal is 1. This could be demonstrated by setting up n algebra tiles in a row and then showing 1 enth of the line always results in a single tile. |
|||||||||||||||||
| 11 | B |
Objective 002 Correct Response: B. Let a vertical position of 0 represent sea level and negative integers represent the depth of the submarine. In this reference system, the integer negative 375 describes the initial position of the submarine. The expression negative 375 + 183 − 228 represents new position of the submarine after it rises and then dives again. It evaluates to negative 420 feet. If the submarine rises at 30 feet per second, then it reaches the surface in 420 divided by 30 = 14 seconds. Incorrect Response: A. This result can be obtained from the expression negative 375 − 183 + 228 . In this case, the submarine starts at a depth of 375, sinks 183 more feet, and then rises 228 feet. Incorrect Response: C. This result is approximately equal to (375 + 228) divided by 30. Incorrect Response: D. This result can be obtained from the expression 375 + 183 + 228. Because integer signs are not considered, this expression represents a submarine that dives by 183 feet and then by 228 feet. |
|||||||||||||||||
| 12 | D |
Objective 002 Correct Response: D. Let x represent the original price of the television. The price after a 15% discount is 0.85x. The tax is paid on the price after discount, so it can be represented by 0 point 0 6 5 times 0 point 8 5 x. The total price paid including discount and tax is 0 point 8 5 x plus 0 point 0 6 5 times 0 point 8 5 x equals 0 point 8 5 x times the quantity 1 plus 0 point 0 6 5 equals k. Solving for x results in x equals k divided by the product of 0 point 8 5 and the quantity 1 plus 0 point 0 6 5. Incorrect Response: A. This response provides the final cost of the television if K represents its initial amount. K, however, represents the final amount. Incorrect Response: B. This expression attempts to reverse the effects of applying tax and providing a discount but does so incorrectly. Consider the claim that a 6.5% increase can be offset with a 6.5% decrease. The multiplication x times the quantity 1 plus 0 point 0 6 5 times the quantity 1 minus 0 point 0 6 5 does not return x. Because the increase of 6.5% was applied with the multiplication of the quantity 1 plus 0 point 0 6 5, it must be removed with the inverse operation of division by that same amount. The same argument applies to the factor of the quantity 1 plus 0 point 1 5 that is used to compensate for the discount. Incorrect Response: C. This equation is the result of solving the equation 0 point 8 5 x times the quantity 1 minus 0 point 0 6 5 equals K for x. The quantity 1 minus 0 point 0 6 5 treats the tax as if it discounted the original price, which is not correct. |
|||||||||||||||||
| 13 | C |
Objective 002 Correct Response: C. To convert the decimal 0 point 0 5 repeating to a fraction, let n = 0 point 0 5 repeating and 100n = 5 point 0 5 repeating. The equation 100n − n = 5 point 0 5 repeating − 0 point 0 5 repeating is equivalent to 99n = 5, so n = 5 ninety-ninths. Incorrect Response: A. The decimal form of 5 ninths is 0 point 5 repeating. Incorrect Response: B. The decimal form of 5 nintieths is 0 point 0 5 repeating. It may be instructive to note that 5 nintieths = 5 ninths divided by 10 and then compare this decimal to the decimal shown in the rationale for response A. Incorrect Response: D. This result may be obtained from the equation 100n − 10n. Notice that the repeating decimals in 100n = 5 point 0 5 repeating and 10n = 0 point 5 repeating will not cancel each other out when they are subtracted. |
|||||||||||||||||
| 14 | C |
Objective 002 Correct Response: C. The prime factorization of 1250 is 2 times 5 to the fourth. Any fraction that only has factors of 2 and 5 in its denominator after it is reduced will be represented with a terminating decimal. Incorrect Response: A. The prime factorization of 270 is 2 times 3 cubed times 5. The multiple factors of 3 present in the denominator cause the decimal equivalent of the fraction to be nonterminating. Incorrect Response: B. The prime factorization of 450 is 2 times 3 squared times 5 squared. The multiple factors of 3 present in the denominator cause the decimal equivalent of the fraction to be nonterminating. Incorrect Response: D. The prime factorization of 3250 is 2 times 5 cubed times 13. The factor of 13 present in the denominator causes the decimal equivalent of the fraction to be nonterminating. |
|||||||||||||||||
| 15 | C |
Objective 002 Correct Response: C. If the GCF of x and y is 3, then x and y can be represented by 3k and 3m, respectively, where k and m are relatively prime (i.e., they share no common factors, otherwise the GCF of x and y would reflect those factors and be greater than 3). Substituting this into 2 over x = 5 over y equals 2 over 3 k = 5 over 3 m. The least common denominator for these fractions is 3km. Given that 3k = x and m = y over 3, the least common denominator can also be written as x times y over 3. Incorrect Response: A. This response corresponds to a least common denominator that is the product of all the quantities shown: 2 times 5 times x times y. Incorrect Response: B. This response incorrectly combines information about the GCF with the denominator values of x and y. Incorrect Response: D. This response corresponds to the reciprocal of 2 times 5 over x times y. |
|||||||||||||||||
| 16 | B |
Objective 002 Correct Response: B. Apply algebraic properties of inequality to test whether A plus c over b plus c is greater than A over b is a true statement. The inequality can be rearranged as b times the quantity A plus c is greater than A times the quantity b plus c through multiplication, expanded as A times b plus b times c is greater than A times b plus a times c by the distributive property, and then further reduced to the simple inequality b is greater than A. This result may be interpreted to mean that A plus c over b plus c is greater than A over b is a true statement when b is greater than A. This must be true because the fraction A over b is a proper fraction greater than zero. Incorrect Response: A. The inequality A minus c over b minus c is greater than A over b can be rearranged as b times the quantity A minus c is greater than A times the quantity b minus c. This expands to A times b minus b times c is greater than A times b minus A times c and simplifies to negative b is greater than negative A, which is also equivalent to b is greater than A. However, this cannot be true because we are given that A over b is a proper fraction greater than 0. Incorrect Response: C. Simplify the left side of the inequality to obtain A over b is greater than A over b, which is a false statement. Incorrect Response: D. Observe that A divided by c over b divided by c is equivalent to A over b. The inequality shown is equivalent to the statement A over b is greater than A over b, which is false. |
|||||||||||||||||
| 17 | B |
Objective 002 Correct Response: B. The space probe will reach its destination in 43 million 100 thousand over 35,960 times 24 days (approximately 49.94 days). This may be approximated with compatible numbers as 40 million divided by 40,000 times 25, which reduces to 1,000 divided by 25 = 40. This is close to 50 despite the substantial overestimation of the denominator. Another potential estimate is to round the fraction to 42 million divided by 36,000 times 24 to obtain 42 times 1 million divided by 36 times 24 times 1,000, which may be further estimated as 7 times 1,000 divided by 44 is approximately 1,000 over 20 = 50. Many other estimation strategies are possible. Incorrect Response: A. Consider that 24 times 24 = 576 hours, a little more than half of 1,000 hours. At 1,000 hours, the total distance would be approximately 35,960,000 miles. The distance covered in 24 days represents a little more than half of this amount (i.e., approximately 18 million miles), suggesting that response B is a much better estimate. Incorrect Response: C. Consider that 24 times 24 times 10 = 5,760 hours, which is a little more than half of 10,000 hours. Following the reasoning in the rationale for A, 10,000 hours corresponds to a distance of 350,960,000 miles—nearly 10 times the distance it is expected to cover. Halving this distance to approximately 500 hours still leads to far too great of a distance. Incorrect Response: D. See the rationales for A and C. An additional potential source of error in these computations is in the conversion between miles per hour and miles per day. |
|||||||||||||||||
| 18 | C |
Objective 002 Correct Response: C. The problem can be described by the linear equation 5 plus 0 point 7 5 times x equals 31, where x is the time in seconds that the cyclist has coasted down the hill and 5 is the initial speed for the cyclist at time x = 0. Solving the equation for x: 5 plus 3 fourths x equals 31 implies 3 fourths x equals 26 implies x equals 26 divided by 3 fourths implies x equals 26 times 4 thirds implies x equals 104 over 3 equals 34 and 2 thirds. Incorrect Response: A. This response is the result of the computation the quantity 31 minus 5 times 3 fourths, which represents a misinterpretation of the relationships in the problem. Incorrect Response: B. This answer is the result of the computation 31 divided by 3 fourths, which does not take the initial speed of the cyclist into account. Incorrect Response: D. This answer is the result of the computation 36 divided by 3 fourths, which may be the result of using the equation 3 fourths times x minus 5 equals 31. |
|||||||||||||||||
| 19 | B |
Objective 002 Correct Response: B. The question asks for a reasonable estimate, so it is appropriate to round the values to make computations simpler. The distance could be rounded to 150,000,000 kilometers equals 1 point 5 times 10 to the eighth power kilometers. The distance from Earth to Mars is half of this value, or 0 point 5 times 1 point 5 times 10 to the eighth equals 0 point 7 5 times 10 to the eighth equals 7 point 5 times 10 to the seventh kilometers. Use an estimate of 10 months of travel time to simplify the calculation. Convert 10 months to hours: 10 months times 30 days over 1 month times 24 hours over 1 day equals 7,200 hours. (Note: while not all months have 30 days, it is a reasonable approximation for the situation—especially when the 10 months of travel time is only an estimate.) Divide the distance by the time to obtain 7.5 times 10 to the seventh kilometers divided by 7.2 times 10 cubed hours is approximately 1 times 10 to the fourth kilometers per 1 hour. Incorrect Response: A. Underestimating the amount of time needed for the spacecraft to travel across this distance could lead to this result. For example, computing the speed without factoring in the months leads to the result 0 point 5 times 1 point 5 times 10 to the eighth power divided by the quantity 30 times 24 is approximately 1 times 10 to the fifth power. Incorrect Response: C. Overestimating the time and distance could lead to this result. For example, 1 point 5 times 10 to the eighth divided by the quantity 30 times 365 times 24 is approximately 1 point 7 times 10 cubed. Incorrect Response: D. Overestimating the amount of time needed for the spacecraft to travel across this distance could lead to this result. For example, converting the time to minutes leads to the result 0 point 5 times 1 point 5 times 10 to the eighth divided by the quantity 30 times 24 times 60 is approximately 1 point 7 times 10 squared. |
|||||||||||||||||
| 20 | C |
Objective 002 Correct Response: C. This response shows 3 times 6 eighths equals 18 over 8 equals 2 and 1 fourth. With these values, A b c equals 2 times 1 times 4 equals 8. Incorrect Response: A. This response shows 3 fifths plus 5 fifths plus 3 fifths equals 11 fifths equals 2 and 1 fifth. With these values, A b c equals 2 times 1 times 5 equals 10. Incorrect Response: B. This response shows 3 times 5 sixths equals 15 sixths equals 2 and one half. With these values, A b c equals 2 times 1 times 2 equals 5. Incorrect Response: D. This response shows 1 fourth plus 3 fourths plus 1 fourth equals 5 fourths equals 1 and 1 fourth. With these values, A b c equals 1 times 1 times 4 equals 4. |
|||||||||||||||||
| 21 | B |
Objective 002 Correct Response: B. The distance between 1 eighth and 3 eighths is 3 eighths minus 1 eighth = 1 fourth unit. This distance is split into 6 segments such that each segment has a length of 1 fourth divided by 6 = 1 twenty-fourth unit. Point D is located 3 segments away from 1 fourth + 3 times 1 twenty-fourth = 1 eighth + 1 eighth = 1 fourth unit. Alternatively, consider that point D is located midway between 1 eighth and 3 eighths, which is 1 fourth. Incorrect Response: A. In this response, Point D is located 3 sevenths of the way from point A to point H. That is, 2 twenty fourths plus 3 sevenths times the quantity 2 thirds minus 2 twenty fourths equals 1 third unit. Incorrect Response: C. In this response, Point D is located 3 fifths of the way from point A to point F. That is, 1 twelfth plus 3 fifths times the quantity one half minus 1 twelfth equals 1 third unit. Incorrect Response: D. In this response, Point D is located 3 fourths of the way from point A to point E. That is, 1 seventh plus 3 fourths times the quantity 3 sevenths minus 1 seventh equals 5 fourteenths unit. |
|||||||||||||||||
| 22 | A |
Objective 002 Correct Response: A. The width of lot A is 4950 divided by 110 = 45 feet, and the width of lot B is 7920 divided by 110 = 72 feet. The ratio 45 to 72 is equivalent to 5 to 8. Incorrect Response: B. This response reflects a ratio that was simplified from 45 over 72 plus 45. It does not compare the correct quantities. Incorrect Response: C. This response represents the ratio of lot B to lot A, but the question asked for the ratio of lot B to lot A. Incorrect Response: D. This response combines the errors described in responses B and C. |
|||||||||||||||||
| 23 | C |
Objective 003 Correct Response: C. The sequence 0, 4, 9.5, 16.5, 25, 35 increases in a quadratic pattern. This can be seen by the linear increase in the first differences: plus4, plus5.5, plus7, plus8.5, plus10 (i.e., the first differences increase by 1.5 with each term). Continuing this pattern leads to a diameter of 6 miles at day 35 + 11.5 = 46.5, a diameter of 7 miles at day 46.5 + 13 = 59.5, and a diameter of 8 miles at day 59.5 + 14.5 = 74. Incorrect Response: A. This response may be based on the reasoning that the diameter of the spill increases at a constant rate of 4 miles every 25 days. This ratio cannot be doubled to 8 miles every 50 days because the diameter of the spill increases more slowly over time. Incorrect Response: B. This response increases the number of days by 10 with each mile of diameter. This represents the difference between 35 days and 25 days. However, the sequence shows that this difference increases as the diameter grows. Repeated addition of 10 does not account for this dynamic. Incorrect Response: D. This response may be based on the reasoning that the square of diameter is approximately equal to the number of days associated with the previous whole number diameter (i.e., 2 squared equals 4, 3 squared is approximately 9 point 5, 4 squared is approximately 16 point 5…). Continuing this pattern, 9 squared is approximately the number of days it takes for the spill to become 8 miles in diameter. This response does not describe the pattern as accurately as response C. |
|||||||||||||||||
| 24 | B |
Objective 003 Correct Response: B. The sequence may be written equivalently as 2 to the power of 0, 2 to the power of 1, 2 squared, 2 cubed, 2 to the fourth power, 2 to the fifth power, and so on. Multiplying two terms in the sequence with values of 2 to the power of a and 2 to the power of b produces 2 to the power of a plus b, which is the value of the term found at position a + b + 1 in the sequence. Incorrect Response: A. The sum of the first two terms proves this claim false. Incorrect Response: C. The average of the first two terms proves this claim false. Incorrect Response: D. This is true only when the division of the two terms produces a whole number, such as when 8 divided by 4 = 2. The quotient of 4 divided by 8 does not appear in the sequence shown. |
|||||||||||||||||
| 25 | B |
Objective 003 Correct Response: B. The value for the first term (when n = 1) is 2 and the sequence decreases by 8 with each new term. The expression that produces 2 for the first term and then decreases by 8 with each additional term is 10 − 8n. Incorrect Response: A. This expression yields 2 minus 8 times 1 equals negative 6 for the first term. It would be correct if the first term corresponded to n = 0 (such as when x = 0 at the y-intercept of a linear equation), but it does not. Incorrect Response: C. This expression yields 8 times 1 minus 2 equals 6 for the first term. Incorrect Response: D. This expression yields 8 times 1 minus 10 equals negative 2 for the first term. |
|||||||||||||||||
| 26 | A |
Objective 003 Correct Response: A. The amount of medication in the patient's bloodstream decreases by 10% each hour, which means that 90% of the medication present at a given moment will still remain in the bloodstream after 1 hour. After the first hour, 100 times 0 point 9 0 equals 90 milligrams remain. After the second hour, 90% of this value remains. This can be expressed as 90 times 0 point 9 0, but it is easier to connect back to the starting value to see the exponential nature of the relationship: 100 times 0 point 9 0 times 0 point 9 0 equals 100 times 0 point 9 0 squared. After t hours, there will be 100 times 0 point 9 0 to the power of t milligrams of medication in the bloodstream. Incorrect Response: B. A linear function changes by a constant rate, so the difference in the amount of medication present in the bloodstream between any two consecutive hours should be the same. This is not what happens. The data below show how a 100 milligram dose of medication will change when only 90% is retained each hour. The difference between any two consecutive hours varies. 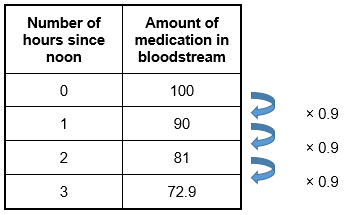 A table with 2 columns and 5 rows. Column 1 head Number of hours since noon. Column 2 head amount of medication in bloodstream. Column 1 row 2 0 column 2 row 2 100. Column 1 row 3 1 column 2 row 3 90. Column 1 row 4 2 column 2 row 4 81. Column 1 row 5 3 column 2 row 5 72.9. Arrows to the right of the table show that data in column 2 changes by times 0.9 for each hour that passes.
A table with 2 columns and 5 rows. Column 1 head Number of hours since noon. Column 2 head amount of medication in bloodstream. Column 1 row 2 0 column 2 row 2 100. Column 1 row 3 1 column 2 row 3 90. Column 1 row 4 2 column 2 row 4 81. Column 1 row 5 3 column 2 row 5 72.9. Arrows to the right of the table show that data in column 2 changes by times 0.9 for each hour that passes.
Incorrect Response: C. A proportional function can be written as f of x equals k times x. In this case, the amount of medication in the bloodstream divided by the number of hours since noon should always produce a constant value. They do not: 90 divided by 1 = 90; 81 divided by 2 = 40.5. Incorrect Response: D. One characteristic of a quadratic function is the difference between two uniformly spaced values will change in a linear pattern. Consider the differences in the pattern below. 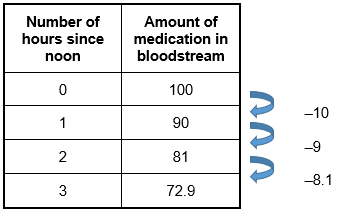 A table with 2 columns and 5 rows. Column 1 head Number of hours since noon. Column 2 head amount of medication in bloodstream. Column 1 row 2 0 column 2 row 2 100. Column 1 row 3 1 column 2 row 3 90. Column 1 row 4 2 column 2 row 4 81. Column 1 row 5 3 column 2 row 5 72.9. Arrows to the right of the table show that data in column 2 changes by minus 10 after the first hour, minus 9 after the second hour, and minus 8.1 after the third hour.
A table with 2 columns and 5 rows. Column 1 head Number of hours since noon. Column 2 head amount of medication in bloodstream. Column 1 row 2 0 column 2 row 2 100. Column 1 row 3 1 column 2 row 3 90. Column 1 row 4 2 column 2 row 4 81. Column 1 row 5 3 column 2 row 5 72.9. Arrows to the right of the table show that data in column 2 changes by minus 10 after the first hour, minus 9 after the second hour, and minus 8.1 after the third hour.
The first difference changes from negative 10 to negative 9 . If this were a linear pattern, the next value should be negative 8, but it is negative 8.1. |
|||||||||||||||||
| 27 | D |
Objective 003 Correct Response: D. A linear relationship is characterized by a constant rate of change. The data in the table show the Celsius measurements increasing by 5 degrees and the Fahrenheit measurements increasing by 9 degrees, and the ratio of these changes is also constant. Incorrect Response: A. A constant relationship describes a situation where the value of one variable does not change when the value of the other variable changes. This is not consistent with the data set. Incorrect Response: B. Mathematical relationships described as quadratic have a rate of change that varies. The data in this table show a constant rate of change. Incorrect Response: C. An exponential relationship is characterized by a constant ratio between successive terms. This does not hold true for these data. Consider the Fahrenheit scale: 50 over 59 does not equal 59 over 68. |
|||||||||||||||||
| 28 | D |
Objective 003 Correct Response: D. In each round, the number of teams remaining in the tournament is halved. There are 256 or 2 to the power of 8 teams in round 1, so 1 half of 2 to the eighth power teams are eliminated in round 1. Then, 128 or 2 to the power of 7 teams remain, so 1 half of 2 to the seventh power teams are eliminated in round 2. At the start of round 3, 64 or 2 to the power of 6 teams remain, so 1 half of 2 to the sixth power games are played in that round. In the first 3 rounds, a total of One half of 2 to the eighth power plus one half of 2 to the seventh power plus one half of 2 to the sixth power implies one half times the quantity 2 to the eighth power plus 2 to the seventh power plus 2 to the sixth power teams have been eliminated. Incorrect Response: A. This response may represent several misconceptions about the number of initial teams or the idea that teams are eliminated in every other round of the tournament. This response is equal to 336 teams, which is greater than the total number of teams in the tournament. Incorrect Response: B. This response may represent a misconception about the number of initial teams in the tournament. This response is equal to 448 teams, which represents the number of teams eliminated in 3 rounds of a tournament with 512 initial teams. Incorrect Response: C. This response correctly calculates the number of teams eliminated in a tournament with 128 initial teams. |
|||||||||||||||||
| 29 | B |
Objective 003 Correct Response: B. Two variables have an inversely proportional relationship when their product is always constant. The product of volume and pressure is constant at 3600 for all the values in the table. The relationship between volume and pressure can best be defined as inversely proportional (i.e., PV = k). Incorrect Response: A. The volume data are increasing uniformly by 5, so we can test for an exponential relationship by determining whether any two consecutive values for pressure have a constant ratio. Consider the three values for pressure at the end of the table: 90 over 100 does not equal 80 over 90. Incorrect Response: C. A linear relationship will have a constant rate of change. The rate of change for the first three coordinate pairs is not constant: 180 minus 144 divided by 25 minus 20 equals 7 point 2, 144 minus 120 divided by 20 minus 15 equals 4 point 8. Incorrect Response: D. One property of quadratic functions is that differences between uniformly spaced values will change in a linear pattern. The difference in the pressure values are negative 36, negative 24, negative 20, negative 10, negative 10; these do not change in a linear pattern. |
|||||||||||||||||
| 30 | B |
Objective 003 Correct Response: B. The dots may be pictured as being arranged in rows and columns.  3 columns of dark dots with 3 dots in the first column, 2 dots in the second column and 1 dot in the last column.
3 columns of dark dots with 3 dots in the first column, 2 dots in the second column and 1 dot in the last column.
Notice that this pattern colors in half of a rectangular array that is R dots wide and R + 1 dots tall.  3 columns of dots. the first column has 1 light dot at the top and three dark dots at the bottom. The second column as 2 light dots at the top and 2 dark dots on the bottom. The third column has 3 light dots at the top and 1 dark dot on the bottom.
3 columns of dots. the first column has 1 light dot at the top and three dark dots at the bottom. The second column as 2 light dots at the top and 2 dark dots on the bottom. The third column has 3 light dots at the top and 1 dark dot on the bottom.
Incorrect Response: A. This equation simplifies to d = R + 3, which means that the number of dots increases by 1 when the number of rows increases by 1. This is not consistent with the pattern. Incorrect Response: C. This equation may be written as d equals 2 thirds r plus 4, which means that the number of dots increases by 2 thirds of a full dot when the number of rows increases by 1. This is not consistent with the pattern. Incorrect Response: D. This may be ruled out as a potential solution by testing this relationship with the second pattern of dots. The equation states that row 4 should contain 2 times 4 squared divided by 3 equals 32 thirds equals 10 and 2 thirds dots. Only whole dots appear in this pattern, so this equation is obviously wrong. |
|||||||||||||||||
| 31 | D |
Objective 004 Correct Response: D. The width of the base of the monument can be represented by 12 minus 4x, since 2x is needed for both the top and bottom sections of the stone path surrounding the base. The length can be represented by 20 minus 2x, since x is needed for both the left and right sections of the stone path. The area of the base of the monument is the quantity 12 minus 4 X times the quantity 20 minus 2 X equals 240 minus 24 X minus eighty X plus 8 X squared equals eight x squared minus 104 X plus 240 = 8 times the quantity X squared minus 13 X plus 30. Incorrect Response: A. This expression represents an expansion of the quantity 20 minus 2 X times the quantity 12 minus X. This is the result of halving the width of the path rather than doubling it to account for the two pairs of sides. Incorrect Response: B. This expression follows from the quantity 20 minus X times the quantity 12 minus 2 X. This does not account for the path having two pairs of sides. Incorrect Response: C. This expression represents an expansion of the quantity 20 minus 4 X times the quantity 12 minus 2 X. |
|||||||||||||||||
| 32 | C |
Objective 004 Correct Response: C. Three liters of a 3% acid solution contains 0 point 0 9 liters of acid. The ratio 0 point 0 9 divided by 3 compares the volume of acid to the total volume of this solution. When x liters of 15% acid solution are added to it, the ratio changes to the quantity 0 point 0 9 plus 0 point 1 5 X all divided by 3 plus X. This ratio equals 0 point 1 2 when the correct amount of acid is added: the quantity 0 point 0 9 plus 0 point 1 5 X all divided by 3 plus X equals 0 point 1 2. Apply the distributive property to obtain 0 point 1 5 x plus 0 point 0 9 equals 0 point 1 2 x plus 0 point 3 6. Incorrect Response: A. The equation 0 point 0 9 x plus 0 point 1 5 equals 0 point 1 2 x has several errors. First, the quantity of 15% acid solution is fixed to 1 liter. To this, x liters of 9% acid is mixed in. The situation modeled by this equation answers a different question: "When is the total amount of acid in 1 liter of 15% acid solution and x liters of 9% acid solution the same as x liters of 12% acid solution?" Incorrect Response: B. The equation 0 point 1 5 x plus 0 point 0 9 equals 0 point 1 2 x plus 3 could be the result of incorrectly applying the distributive property to the quantity 0 point 0 9 plus 0 point 1 5 X all divided by 3 plus X equals 0 point 1 2. Incorrect Response: D. As with incorrect response A, this response can be eliminated because the term 0 point 0 9 x would represent adding 9% acid solution to the mixture. |
|||||||||||||||||
| 33 | B |
Objective 004 Correct Response: B. Substitute 2 fifths for x and then simplify as follows: 2 times 2 fifths to the negative second power minus 4 times 2 fifths to the negative first power equals 2 times five halves squared minus 4 times 5 halves = 2 times 25 fourths minus 4 times 5 halves equals 5 halves Incorrect Response: A. This result could be obtained by misrepresenting the expression as 2 times 2 fifths times negative 2 minus 4 times 2 fifths times negative 1, where the exponent is treated as a multiplication factor. Incorrect Response: C. This result could be obtained by misrepresenting the expression as 1 over the quantity 2 times 2 fifths squared minus 1 over the quantity 4 times 2 fifths, where the exponents are applied to both the variable and the coefficient. Incorrect Response: D. This result could be obtained by misrepresenting the expression as negative 2 times 2 fifths squared plus 4 times 2 fifths, where the negative symbol in the exponent is treated as if it were multiplied by negative 1. |
|||||||||||||||||
| 34 | D |
Objective 004 Correct Response: D. The solution set for the inequality can be found as follows: Original problem: negative 2 thirds times the quantity 3 m minus 2 is less than one half the quantity m plus 1 Apply the distributive property: negative 2 m plus 4 thirds is less than one half m plus 1 half Apply the addition property of inequalities: negative 2 m minus 1 half m is less than one half minus 4 thirds Simplify: negative 5 halves m is less than negative 5 sixths Apply the multiplicative property of inequalities: m is greater than negative 5 sixths times negative 2 fifths Simplify: m is greater than 1 third The graph should have an open circle at 1 third and shading to the right of 1 third. Graph D shows the solution set for the inequality. Incorrect Response: A. One fast way to eliminate this response is by testing a point in the proposed solution set to see whether it satisfies the original inequality. Substituting the point m = negative1 results in the inequality negative 2 thirds times the quantity 3 times negative 1 minus 2 is less than one half times the quantity negative 1 plus 1 implies 10 thirds is less than 0. This is a false statement, so this answer should be eliminated. Incorrect Response: B. One fast way to eliminate this response is by testing a point in the proposed solution set to see whether it satisfies the original inequality. Substituting the point m = 0 results in the inequality negative 2 thirds times the quantity 3 times 0 minus 2 is less than one half times the quantity 0 plus 1 implies 4 thirds is less than one half. This is a false statement, so this answer should be eliminated. Incorrect Response: C. This response could indicate a misconception with the multiplication property of inequalities. Following the steps from the correct response, Original problem: negative 2 thirds times the quantity 3 m minus 2 is less than one half the quantity m plus 1 Apply the distributive property: negative 2 m plus 4 thirds is less than one half m plus 1 half Apply the addition property of inequalities: negative 2 m minus 1 half m is less than one half minus 4 thirds Simplify: negative 5 halves m is less than negative 5 sixths The next step is to multiply both sides of the inequality by negative 2 fifths, so the direction of the inequality must be reversed. The graph in the response could indicate that this change was not applied. |
|||||||||||||||||
| 35 | D |
Objective 004 Correct Response: D. Apply order of operations to evaluate the expression: the quantity 5 plus negative 2 to the fourth divided by 4 times the quantity 5 squared minus negative 2 squared equals 3 to the fourth divided by 4 times the quantity 25 minus 4 equals 81 over 4 times 21 equals 81 80 fourths equals 27 twenty eighths. Incorrect Response: A. The following interpretation of the expression leads to this result: the quantity A plus c to the power of b divided by b times the quantity A squared minus c squared equals the quantity 5 plus negative 2 times 4 divided by 4 times the quantity 25 minus 4 equals 5 minus 8 divided by 4 times 21 equals negative 3 over 84 equals negative 1 over 28. Incorrect Response: B. The following interpretation of the expression leads to this result: the quantity A plus c to the power of b divided by b times the quantity A squared minus c squared equals b times the quantity A plus c divided by b times the quantity 2 A minus 2 c squared equals 4 times the quantity 5 minus 2 over 4 times the quantity 10 minus 4 equals 3 sixths. Incorrect Response: C. An incorrect application of operations in the denominator could develop the expression the quantity 5 plus negative 2 to the fourth power divided by 4 times the quantity 25 plus 4, which simplifies to the response 81 1 hundred sixteenths. |
|||||||||||||||||
| 36 | A |
Objective 005 Correct Response: A. The middle graph shows that can C weighs less than can B, and the left graph shows that can B weighs less than can A. Therefore, can C weighs the least. Incorrect Response: B. The left graph shows that cans A and B do not have the same height. Incorrect Response: C. The middle graph shows that can C is more expensive than can B. Incorrect Response: D. The right graph shows that can C is taller than can A. |
|||||||||||||||||
| 37 | D |
Objective 005 Correct Response: D. The water takes on the shape of the vessel into which it is poured. When V units of water have been poured into a cylinder of radius r and height h, the height and volume of the water column are related by the equation V equals pi r squared times h. The volume may be substituted by kt to account for the water being added at a constant rate k over time t. This changes the original equation to k times t equals pi r squared times h, which can also be rearranged as h equals k divided by pi r squared times t. The form of the equation clearly shows that the height of the water increases at a constant rate for each segment and that the segment with the largest radius has the smallest slope. Incorrect Response: A. This graph could be used to describe the height of water as it is poured into a cylinder but does not account for variations in the width of the vessel. Incorrect Response: B. The height of this graph increases more quickly over time. This would happen if the shape of the container was constantly narrowing, such as with a cone or a pyramid shape. The vessel shown does not have this characteristic. Incorrect Response: C. The shape of the curve would match a curvy vessel shape that smoothly narrows and widens along its height. The vessel shown does not have this characteristic. |
|||||||||||||||||
| 38 | D |
Objective 005 Correct Response: D. The graph of the function f of x plus 5 represents the horizontal translation of the graph of function f of x b units to the left. The function g of x = function f of x plus 5 has a graph that is identical in shape to that of function f of x but is shifted to the left by 5 units. Incorrect Response: A. This response may indicate a misconception in the direction of a shift. If function f of x minus 5 were incorrectly interpreted to mean an upward shift of function f of x by 5 units, then the quantity x plus 5 squared could be interpreted to mean that x squared was shifted down by 5 units. Incorrect Response: B. This response may indicate a misconception in the direction of a shift. Interpreting function f of x plus 5 to mean a shift of function f of x to the right by 5 units would lead to this result. Incorrect Response: C. This response may indicate a misconception either in the direction of a shift or with the order of operations. Subtracting function g of x minus 5 gives the quantity x plus 5 squared minus 5 equals x squared plus 10 x plus 25 minus 5 equals x squared plus 10 x plus 20. This is not equal to function f of x. |
|||||||||||||||||
| 39 | C |
Objective 005 Correct Response: C. A Cartesian plane displays the input values for a relation on the horizontal axis and the output values on the vertical axis. A function is a relation that has one output value for each input value, which this response shows. Incorrect Response: A. This response does not show one output value associated with each input value (i.e., one y-coordinate associated with each x-coordinate), so this graph cannot represent a function. Incorrect Response: B. This response does not show one output value associated with each input value (i.e., one y-coordinate associated with each x-coordinate), so this graph cannot represent a function. Incorrect Response: C. This response does not show one output value associated with each input value—the vertical segments span an infinite number of y-values as they drop down to the x-axis—so this graph cannot represent a function. |
|||||||||||||||||
| 40 | A |
Objective 005 Correct Response: A. The slope of each segment indicates the speed of the car in that segment. The car initially moves quickly and then slows down, speeds up, and slows down again. This is consistent with the description that the car began on the highway, slowed down in traffic, returned to highway speeds, and then slowed down on local roads. The constant slope back to the horizontal axis represents the steady rate home on local roads. Incorrect Response: B. This response shows the distance from home always increases over time. However, the information states that the car returned home. A correct graph must show the car has 0 distance from home at the end of its journey. Incorrect Response: C. This response shows the car returns home from its destination instantly. This is not what happened. Incorrect Response: D. This response is similar to that of response B in that it shows the distance from home always increasing over time; however, the information states that the car returned home. |
|||||||||||||||||
| 41 | B |
Objective 006 Correct Response: B. If one variable varies directly as another, then the ratio of the two variables is a constant. As one variable doubles, so will the other. Given that (x, y) is one point on the graph of f of x, doubling the x value will result in doubling the y value, regardless of the value of the constant of variation. Another point on the graph of f of x will be (2x, 2y). Incorrect Response: A. This answer can be disproved by testing the coordinate point (1, negative 2 thirds). The resulting equation shows that the constant of variation is not equal to negative 2 thirds: 2 y over negative 2 x equals a fraction with 2 times negative 2 thirds in the numerator and negative 2 times 1 in the denominator equals a fraction with negative 4 thirds in the numerator and negative 2 in the denominator equals 4 sixths equals 2 thirds does not equal negative 2 thirds. From the given information, the y-coordinate must be negative 1 times the x-coordinate. The given information also states that the coordinate (x, y) follows this relationship. If the equation y equals negative x is balanced, then the equation 2 y equals negative 2 thirds times negative 2 x is not. Incorrect Response: C. This answer can be disproved by testing the coordinate point (1, negative 2 thirds). The resulting equation shows that the constant of variation is not equal to negative 2 thirds: 3 y over negative 2 x equals a fraction with 3 times negative 2 thirds in the numerator and negative 2 times 1 in the denominator equals negative 2 over negative 2 equals 1 does not equal negative 2 thirds. Incorrect Response: D. From the given information, the y-coordinate must be negative 2 thirds times the x-coordinate. The given information also states that the coordinate (x, y) follows this relationship. If the equation y equals negative 2 thirds x is balanced, then the equation 3 y equals negative 2 thirds times 2 x is not. |
|||||||||||||||||
| 42 | D |
Objective 006 Correct Response: D. The ratio of number of students over number of teachers equals x over y equals 20 over 3, so 3 x equals 20 y or y equals 3 twentieths x. The graph of y equals 3 twentieths x is a line through the origin with slope equal to 3 twentieths. Graph D goes through (0, 0) and (100, 15) and has a slope of 15 hundredths equals 3 twentieths. Incorrect Response: A. This graph indicates that 12 teachers on a field trip would chaperone 0 students and that 80 students on a field trip would have 0 chaperones. This is not consistent with the situation. Incorrect Response: B. This graph indicates that 60 teachers on a field trip would chaperone 0 students and that 9 students on a field trip would have 0 chaperones. This is not consistent with the situation. Incorrect Response: C. This graph indicates that 200 teachers would chaperone 30 students, which is likely the result of interpreting the y-values to represent the number of students and the x-values to represent the number of teachers. |
|||||||||||||||||
| 43 | C |
Objective 006 Correct Response: C. Line L moves from negative 2, k plus 8 to 2, k by moving down by 8 units and right by 4 units. Therefore, the slope of the line is negative 2. The x-intercept of the line occurs where the value of the y-coordinate is 0. If the line starts from the point negative 2, k plus 8, then it reaches its x-intercept by moving down by k plus 8 and to the right by half this distance. Its final position is negative 2 plus 1 half k plus 8, and this expression is equivalent to 1 half the quantity k plus 4. Incorrect Response: A. This expression represents the location of the y-intercept. The line moves 2 units to the right and 4 units down from the point negative 2, k plus 8 to reach its y-intercept of 0, k plus 4. Incorrect Response: B. This expression may be the result of the reasoning described in the rationale for response A along with a sign error. Incorrect Response: D. This expression may be the result of the reasoning described in the rationale for response C along with a sign error. |
|||||||||||||||||
| 44 | C |
Objective 006 Correct Response: C. The slopes of parallel lines are equal. The slope of 3 x plus a y equals b can be found by solving the equation for y in terms of x: 3 x plus a y equals b implies a y equals negative 3 x plus b implies y equals negative 3 over a times x plus b over a. Using point-slope form, y minus y 1 equals m times the quantity x minus x 1, slope m = negative 3 over A and point X 1, y 1 equals negative 4, 0 yields y equals negative 3 over a times the quantity x plus 4 for the equation of line p. Incorrect Response: A. The slope of a line written in the standard form A x plus b y equals c is negative A over b. This response could be the result of calculating the slope of the first equation as A divided by b. Incorrect Response: B. This could be the result of combining the error described in response A and by misapplying the distributive property. Incorrect Response: D. This could be the result of a distributive property error while applying the point-slope equation. |
|||||||||||||||||
| 45 | B |
Objective 006 Correct Response: B. The graph of negative 2 times the quantity x minus 3 is less than y plus 7 is equivalent to y is greater than negative 2 x minus 1 and passes through the point (3, negative 7) with a slope of negative 2. The inequality is shown as a dashed line because values of y cannot be equal to those represented by the expression of x. The inequality holds true for any point within the region above this line. The graph of 3 x minus 4 y is greater than or equal to 12 is equivalent to y is less than or equal to 3 fourths x minus 4 and passes through the x-axis at (4, 0) and the y-axis at (0, negative 3). The inequality is represented as a shaded region below a solid line. The solution to the system of inequalities is the region two individual inequalities overlap, as shown in response B. Incorrect Response: A. This response shows the system of inequalities negative 2 times the quantity x minus 3 is greater than y plus 7 is equivalent and 3 x minus 4 y is greater than or equal to 12. Incorrect Response: C. This graph shows the solution to the system of inequalities 3 x minus 4 y is greater to 12 and negative 2 times the quantity x minus 3 is less than or equal to y plus 7. Incorrect Response: D. This graph shows the solution to the system of inequalities 3 x minus 4 y is greater to 12 and negative 2 times the quantity x minus 3 is greater than or equal to y plus 7. |
|||||||||||||||||
| 46 | A |
Objective 006 Correct Response: A. The solution can be found using elimination: 3 x plus 4 y equals negative 20 implies 3 times the quantity 3 x plus 4 y equals negative 20 implies 9 x plus 12 y equals negative 60 2 x minus 3 y equals negative 2 implies 4 times the quantity 2 x minus 3 y equals negative 2 implies 8 x minus 12 y equals negative 8 Note that the multipliers of 3 and 4 were used for the purpose of canceling the y terms. Adding the two remaining equations produces the correct response: 9 x plus 12 y equals negative 60 plus 8 x minus 12 y equals negative 8 implies 17 x equals negative 68 implies x equals negative 4 Incorrect Response: B. This response represents the y-value in the solution to the system of equations. Incorrect Response: C. This could be the result of errors related to distributing the factors of 3 and 4 to all terms in the original equations. 3 x plus 4 y equals negative 20 implies 3 times the quantity 3 x plus 4 y equals negative 20 implies 3 x plus 12 y equals negative 20, 2 x minus 3 y equals negative 2 implies 4 times the quantity 2 x minus 3 y equals negative 2 implies 2 x minus 12 y equals negative 8, implies 5 x equals negative 28 Incorrect Response: D. This could be the result of multiplying the equations by 3 and 4 (as shown in the rationale for response A) but not distributing the multiplication to the constant terms on the right of the equal sign: 3 x plus 4 y equals negative 20 implies 3 times the quantity 3 x plus 4 y equals negative 20 implies 9 x plus 12 y equals negative 20 2 x minus 3 y equals negative 2 implies 4 times the quantity 2 x minus 3 y equals negative 2 implies 8 x minus 12 y equals negative 2 |
|||||||||||||||||
| 47 | C |
Objective 006 Correct Response: C. The two constraints in this problem are the maximum weight the shelf can hold and the length of the shelf. The shelf can hold up to, and including, 85 pounds. Given that x represents the number of textbooks that weigh 6 pounds each and y represents the number of lab manuals that weigh 5 pounds each, this constraint is modeled by the inequality 6 x plus 5 y is less than or equal to 85. The shelf is 3 feet, or 36 inches, long, textbooks are 2 inches thick, and lab manuals are 2.5 inches thick. This constraint is modeled by the inequality 2 x plus 2 point 5 y is less than or equal to 36. Incorrect Response: A. Because the bookshelf "can hold up to 85 pounds," the symbol less than or equal to should be used. This symbol should also be used for the combined textbook lengths, which could be exactly 3 feet long and still fit on the bookshelf. Incorrect Response: B. The number 85 on the right side of the inequality represents the combined weights of the two books. The two terms added together on the left side of the inequality should also represent weight. However, if x is the weight of the book, then dividing that weight by 6 pounds per book yields units of books rather than pounds. Incorrect Response: D. The error in this response is similar to the one described in the rationale for response B. |
|||||||||||||||||
| 48 | B |
Objective 006 Correct Response: B. A family of lines is a set of lines that have something in common with each other. The set of lines shown in the graph all contain the point (2, negative 3). The point-slope form of a linear equation is y minus y 1 equals m times the quantity x minus x 1, where m is the slope of the line and x 1, y 1 is a point on the line. In this case, the slope of the lines is the parameter k, and the point is (2, negative 3). The equation for the family of lines is y minus negative 3 equals k times the quantity x minus 2, or y plus 3 equals k times the quantity x minus 2. Incorrect Response: A. The equation y plus 3 equals k x minus 2 can be rearranged as y equals k x minus 5. If this were true, then by the point-slope formula, the common point of intersection for the lines would be located at (0, negative 5). Incorrect Response: C. The equation y equals k x plus 2 minus 3 simplifies as y plus 1 equals k x. If this were true, then the common point of intersection for the lines would be located at (0, negative 1). Incorrect Response: D. The equation y equals k times the quantity x plus 2 minus 3 can be rearranged as y plus 3 equals k times the quantity x plus 2. If this were true, then the common point of intersection for the lines would be located at (negative 2, negative 3). |
|||||||||||||||||
| 49 | C |
Objective 006 Correct Response: C. From the table, y decreases by 2 thirds when x increases by 1. Continue the pattern back by 1 to identify a y-intercept of 4. In slope-intercept form, the equation for the line is y equals negative 2 thirds x plus 4. This equation may be transformed to standard form: 2 thirds x plus y equals 4 implies 2 x plus 3 y equals 12. Incorrect Response: A. This response is incorrect because it does not hold true when the variables are substituted with values from the table: 1 minus 3 times 3 and 1 third equals negative 9 does not equal 6. Incorrect Response: B. This response could be formed by observing that the relationship for the second row of the table may be expressed as 1 third x plus 2 equals y implies 3 y minus x equals 6. Incorrect Response: D. This response is likely the result of applying the slope to the wrong variable or making a mistake with the format for slope-intercept form: X equals negative 2 thirds y plus 4 implies x plus 2 thirds y equals 4 implies 2 y plus 3 x equals 12. |
|||||||||||||||||
| 50 | D |
Objective 007 Correct Response: D. The sequence of values for this vehicle is 27,500 dollars in the current year, 27,500 dollars divided by 1 minus 0 point 1 5 one year ago, 27,500 dollars divided by 1 minus 0 point 1 5 the quantity squared two years ago, and 27,500 dollars divided by 1 minus 0 point 1 5 the quantity cubed three years ago. Incorrect Response: A. This response represents the future value of 27,500 dollars if it increased in value by 15% every year for three years. Incorrect Response: B. This response represents the future value of 27,500 dollars if it decreased in value by 15% every year for three years. Incorrect Response: C. This response would represent the previous value of the car if it had increased in value by 15% every year for three years. |
|||||||||||||||||
| 51 | C |
Objective 007 Correct Response: C. When the equation for a parabola is written in the form y equals A times the quantity x plus b times the quantity x plus c, the x-intercepts of the parabola are located at (negative b, 0) and (negative c, 0). The x-intercepts of the parabola shown in the graph are at (negative 4, 0) and (negative 1, 0) so b = 4 and c = 1, making the equation y equals A times the quantity x plus 4 times the quantity x plus 1. According to the graph, the y-intercept of the parabola is (0, negative 1). Use this point to solve the equation for A: negative 1 equals A times 4 times 1 implies A equals negative 1 fourth. Incorrect Response: A. This response represents the width between the two roots. Incorrect Response: B. This response represents the value of the y-intercept. Incorrect Response: D. This response may be the result of estimating the y-value of the vertex to be negative 1 half and then assigning that value to A. |
|||||||||||||||||
| 52 | A |
Objective 007 Correct Response: A. Let x represent the length of one side of the square pen and x squared the area of the pen. Increasing the length of one side by 4 meters and the other side by 2 meters creates a rectangle with length x plus 4 and width x plus 2. The new area, x plus 4 times x plus 2, is three times the old area, 3 x squared. Solving the equation x plus 4 times x plus 2 equals 3 x squared will yield the value of x. First, distribute to multiply the binomials: x squared plus 4 x plus 2 x plus 8 equals 3 x squared. Then combine like terms and use the addition property of equality to set the equation equal to 0: 2 x squared minus 6 x minus 8 equals 0. Use the multiplication property of equality to simplify the equation by a factor of 2: x squared minus 3 x minus 4 equals 0. Incorrect Response: B. This equation represents the expansion of x plus 4 times x plus 2 equals 0. The area of the rectangular pen is not zero. Incorrect Response: C. This equation may represent the sum of the new and expanded pens: x squared plus the quantity x plus 4 times the quantity x plus 2 equals 0. Incorrect Response: D. This equation may come from the equation 2 x plus 4 equals 3 x squared. |
|||||||||||||||||
| 53 | A |
Objective 007 Correct Response: A. Substitute c, representing the y-intercept, into the equation to get y equals x squared plus b x minus 36. The information given states that (3, 0) is also a point. Substitute this into the equation to determine the unknown value of b: 0 equals 3 squared plus b times 3 minus 36 implies 3 b equals 27 implies b equals 9. Obtain the other root by factoring the y equals x squared plus 9 x minus 36 as y equals the quantity x minus 3 times the quantity x plus 12. The other root is located at (negative 12, 0). Incorrect Response: B. A sign error, such as one developed from substituting c = 36 into the equation could lead to this response. For example, 0 equals 3 squared plus b times 3 plus 36 implies 3 b equals negative 27 implies b equals negative 9. Incorrect Response: C. This response could represent the value obtained for bx when (3, 0) is substituted into the equation y equals x squared plus b x minus 36: 0 equals 3 squared plus 3 times 3 minus 36. Incorrect Response: D. A sign error, such as one developed from factoring y equals x squared plus 9 x minus 36 as y equals the quantity x plus 3 times the quantity x minus 12 could lead to this response. |
|||||||||||||||||
| 54 | C |
Objective 008 Correct Response: C. The base of the cone is a circle. The net of the lateral surface of a cone is represented as a 60 degrees sector of a circle 10 centimeters in radius. It follows that the curved edge of the cone has a length of 1 sixth times 2 pi times 10 equals 10 pi divided by 3. This distance fully wraps around the circle at the base. To find the radius of that circle, set its circumference equal to the length of the curved edge of the lateral side and solve for r: 10 pi divided by 3 equals 2 pi r implies r equals 10 sixths which equals 5 thirds. The area of the circle is then pi times 5 thirds squared equals 25 ninths pi. Incorrect Response: A. This answer is the result of not applying the square to both the numerator and the denominator in the final step of the solution shown for response C. Incorrect Response: B. This response is the result of misinterpreting the radius of the circle to be 5 sixths, and then applying the power of 2 only to the numerator in the final step of the solution process shown for response C. Incorrect Response: D. Making an error when solving for r in the solution shown for response C could lead to r = 5 sixths, which results in an answer of 25 pi divided by 36. |
|||||||||||||||||
| 55 | A |
Objective 008 Correct Response: A. The ratio for the smaller cube is surface area divided by volume equals 6 x squared divided by x cubed. The ratio for the larger cube is surface area divided by volume equals 6 times 4 x squared divided by 4x cubed equals 16 times 6 x squared divided by 64 x cubed equals 1 fourth times 6x squared divided by x cubed. In general, scaling the linear dimensions of a shape by k increases its surface area by a factor of k squared and its volume by a factor of k cubed. The ratio of these two values is k. Incorrect Response: B. This response may indicate a misconception with the relationship between a linear dimension of a shape and its surface area and volume. Incorrect Response: C. This response may indicate a misconception with the relationship between a linear dimension of a shape and its surface area and volume. Incorrect Response: D. This response represents the reciprocal of the correct ratio. |
|||||||||||||||||
| 56 | D |
Objective 008 Correct Response: D. When limited to a precision of 2 decimal places, the maximum overestimation possible in the edge of a cube is 10.49 inches. This leads to a maximum error in volume of 10 point 49 cubed minus 10 cubed. Incorrect Response: A. This represents the cube of the difference between the two side lengths. This does not represent the difference in the volumes of the two cubes. Incorrect Response: B. At a precision of 0.01 inches, the greatest overestimate for the volume occurs when using 10 inches for a cube that has a true edge length of 9.5 inches and the greatest underestimate when the true edge length is 10.49 inches. In both cases, the error is relative to using the rounded value of 10 inches and not to each other. This misconception is further compounded with reasoning described in the rationale for response A. Incorrect Response: C. A cube with an edge length of 9.5 inches is the smallest cube that would round up to an edge length of 10 inches. A cube of 9.4 inches would round to 9 inches, not 10, and so this calculation does not apply to this situation. |
|||||||||||||||||
| 57 | B |
Objective 008 Correct Response: B. Split triangle T A B into two right triangles by drawing the radius that is perpendicular to A B. The perpendicular chord bisector theorem states that this radius bisects chord A B. Given that the legs formed by the bisected chord are congruent, the radius bisecting them is shared by both triangles, and the two other radii form a pair of congruent hypotenuses, these triangles are congruent by S S S. Therefore, the 140 degrees is bisected into two angles that are each 70 degrees, and the length of each bisector of highway A B is 50 sine 70 degrees. The length of A B is twice this value. Incorrect Response: A. This response uses twice the correct value of the angle and half the correct value for the coefficient. Compare with response B. Incorrect Response: C. This response uses the reasoning described in response A and also uses an incorrect trigonometric function. In this context, cosine 70 degrees is equal to the ratio of the length of the leg adjacent to the angle of 70 degrees and the hypotenuse of the triangle. Incorrect Response: D. This response uses the reasoning described in responses A and C. |
|||||||||||||||||
| 58 | D |
Objective 008 Correct Response: D. The situation in the question can be modeled with the following diagram: 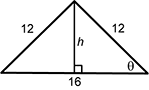 isosceles triangle with a base angle theta, a base of length 16, and legs of length 12 and height h
isosceles triangle with a base angle theta, a base of length 16, and legs of length 12 and height h
The area of a triangle equals 1 half times base times height. The base is 16, so 1 half times base equals 8. To find the height of the triangle, use the fact that sine of theta equals h over 12 implies h equals 12 times sine of theta. The area of the triangle is then 8 times 12 times sine of theta equals 96 times sine of theta. Incorrect Response: A. This answer is the result of both errors shown in the rationales for responses B and C. It is the result of using cosine instead of sine to find the height of the triangle, and unnecessarily halving the result. Incorrect Response: B. This answer is the result of misinterpreting the relationship between theta and the height of the triangle and using cosine instead of sine. Incorrect Response: C. This answer is the result of halving the answer shown in the rationale for Response D. It is likely the misinterpretation of the 1 half in the formula for the area of a triangle. |
|||||||||||||||||
| 59 | A |
Objective 009 Correct Response: A. When solving geometric proofs, one can assume that points that appear to be collinear in a diagram are collinear. Thus, the assumption that can be made regarding the figure shown is that point A is on segment D C. Incorrect Response: B. This is true if triangle A B C is equilateral, but there is no evidence in the diagram to support this claim. Incorrect Response: C. There is no information provided in the diagram that supports that segment B D is perpendicular to segment A C. Incorrect Response: D. There is no evidence to support this, such as congruency between alternate interior angles, in the image provided. |
|||||||||||||||||
| 60 | C |
Objective 009 Correct Response: C. Construct a line parallel to line L through point B. This line will also be parallel to line m. 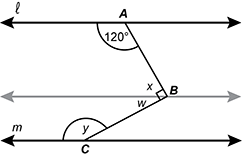 The image from the stem is shown, with an additional horizontal line passing through point B in the interior of the parallel lines. This horizontal line divides angle b into two complementary angles: x on the top, and w on the bottom.
The image from the stem is shown, with an additional horizontal line passing through point B in the interior of the parallel lines. This horizontal line divides angle b into two complementary angles: x on the top, and w on the bottom.
The angle labeled x will be supplementary to the 120 degree angle, so the measure of the angle labeled x is 60 degrees. The sum of the angles labeled x and w is 90 degrees, so the measure of the angle labeled w is 30 degrees. The angle labeled w will be supplementary to the angle labeled y, so the measure of the angle labeled y is 150 degrees. Incorrect Response: A. If the segments that form angle B were congruent, then angle y would have the same measure as angle A, but this cannot be deduced from the image shown. Incorrect Response: B. This response may be the result of creating a 45 45 90 triangle within the diagram, and then attempting to use one 45-degree angle to find its supplement, 135 degrees. Incorrect Response: D. Like response B, this may be the result of misapplying properties of 45 45 90 triangles in the diagram. In this case, 45 degrees was added to 120 degrees to get 165 degrees. |
|||||||||||||||||
| 61 | D |
Objective 009 Correct Response: D. Consider the following diagram. 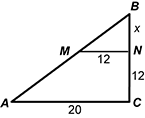 Right triangle A b c with line segment m n intersecting the vertical side and the opposite side to create a smaller triangle m b n. Side a c is 20, m n is 12, c n is 12, and n b is x.
Right triangle A b c with line segment m n intersecting the vertical side and the opposite side to create a smaller triangle m b n. Side a c is 20, m n is 12, c n is 12, and n b is x.
Triangles A B C and M B N are similar by the triangle proportionality theorem (i.e., the corresponding sides are parallel because M N is parallel to A C and intersects the sides of triangle A B C). This establishes the proportion x over 12 equals x plus 12 over 20 and the equation 12 times the quantity x plus 12 equals 20 x. Determine x from the equation 12 x plus 144 equals 20 x implies 8 x equals 144 implies x equals 18. The length of side segment C B is 18 plus 12 = 30. Incorrect Response: A. This response may represent a misconception about similarity. If the triangles were considered to be related by subtraction, then 20 minus 12 = 8 and 12 minus 8 = 4; segment C N = 12 + 4. However, similar triangles are related by multiplicative scale factors and not the subtraction shown here. Incorrect Response: B. This represents the length of segment N B. It must be added to the length of segment C N to obtain the length of segment C B. Incorrect Response: C. This response may be based on an incorrect claim that segment A C and segment C B are congruent. |
|||||||||||||||||
| 62 | A |
Objective 009 Correct Response: A. Using the diagram and the information given about the diagram, the following can be proven: 2 columns and 8 rows
The statement that is a true deduction based on the given information is segment D X is congruent to segment B X. Incorrect Response: B. Kite A B C D could satisfy the given information, which would mean that it is not necessarily true that both diagonals are perpendicular bisectors of each other. This means that segment A X does not have to be congruent to segment C X. Incorrect Response: C. This statement is only true when A B C D is a square. Since a square is not the only shape to satisfy the given criteria, this statement is not necessarily true. Incorrect Response: D. This statement is only true when segment A D is parallel to segment B C. If the figure is a kite, then these segments are not parallel. |
|||||||||||||||||
| 63 | B |
Objective 009 Correct Response: B. Quadrilateral P R S U is proven to be a parallelogram by noting that the opposite angles are congruent. By corresponding parts of congruent figures, angle d is congruent to angle h and angle a is congruent to angle e. Therefore, quadrilateral P R S U is a parallelogram, and segment P U is parallel to segment R S by the definition of a parallelogram. Incorrect Response: A. The length of these two segments does not directly prove parallelism between segment P U and segment R S. Incorrect Response: C. Use of the segment addition postulate is insufficient to prove parallelism between segment P U and segment R S. Incorrect Response: D. This claim can be used to show that consecutive angles in quadrilateral P R S U are supplementary, which is a sufficient starting point to conclude that quadrilateral P R S U is a parallelogram. Proving this requires several intermediate steps, making this method less efficient for proving that segment P U is parallel to segment R S. |
|||||||||||||||||
| 64 | C |
Objective 010 Correct Response: C. The sum of the measures of central angles of a semicircle is 180 degrees, so the angle labeled is 180 minus the quantity 60 plus 20 plus 70 equals 30 degrees. Using properties of vertical angles, angle P O Q is equal to 50 degrees. Since triangle P O Q has two sides formed by radii of the circle, the triangle is isosceles. If two sides in a triangle are congruent, then the angles opposite the congruent sides are also congruent angles. Since interior angles in a triangle sum to 180°, 180 minus 50 equals 2 times the measure of angle O P Q, which implies that angle O P Q has a measure of 65 degrees. Incorrect Response: A. If the measure of angle P O Q is interpreted to be 70 degrees, then isosceles triangle properties used in the rationale for response C would lead to a result of 55 degrees for angle O P Q. Incorrect Response: B. If the measure of angle P O Q is interpreted to be 60 degrees, then isosceles triangle properties used in the rationale for response C would lead to a result of 60 degrees for angle O P Q. Incorrect Response: D. If the measure of angle P O Q is interpreted to be 30 degrees, then isosceles triangle properties used in the rationale for response C would lead to a result of 70 degrees for angle O P Q. |
|||||||||||||||||
| 65 | B |
Objective 010 Correct Response: B. The volume of the cube is v equals 2 r cubed equals 8 r cubed equals 64 cubic inches. Divide 8 r cubed equals 64 by 8 to obtain r cubed equals 8. The value of r is the cube root of 8, which is 2. This is the radius of the sphere, which has a volume of v equals 4 thirds pi r cubed equals 4 thirds pi times 2 cubed equals 32 pi over 3. The value of π is little more than the value of 3pi divided by 3 is approximately 1.04, so the approximation of the volume as 33 cubic inches is reasonable. Incorrect Response: A. This response is the result of using the reciprocal of 4 thirds in the calculation for the volume of the sphere: v equals 3 fourths times pi times 2 cubed equals 6 pi which is approximately 19. Incorrect Response: C. This could be obtained by overestimating the value of pi over 3 in the equation. Incorrect Response: D. Using 4 pi r squared for volume gives 4 pi times 2 squared equals 16 pi, which is approximately equal to this answer. |
|||||||||||||||||
| 66 | B |
Objective 010 Correct Response: B. The top section of the rotated figure will be a hemisphere with radius z. The volume of the hemisphere is 1 half times 4 thirds times pi times z cubed equals 2 thirds pi times z cubed. The bottom section of the solid will be a cylinder with radius z and height 2 z. The volume of the cylinder is pi times z squared times 2 z equals 2 pi z cubed. The volume of the rotated figure is 2 thirds times pi times z cubed plus 2 pi z cubed equals 2 thirds pi z cubed plus 6 thirds pi z cubed equals 8 pi z cubed over 3. Incorrect Response: A. This is the result of quartering the volume of the hemisphere instead of halving it. This leads to a volume for the hemisphere of 1 third times pi times z cubed, which results in a total volume calculation of 1 third pi z cubed plus 2 pi z cubed equals 7 pi z cubed divided by 3. Incorrect Response: C. Forgetting to multiply the formula for the volume of a sphere by 1 half will result in the calculation of 4 thirds times pi times z cubed for the volume of the hemisphere, which leads to the result 4 thirds pi z cubed plus 2 pi z cubed equals 10 pi z cubed divided by 3. Incorrect Response: D. If the 1 half is removed from the volume calculation for the hemisphere, and the radius of the hemisphere is interpreted to be 2 z, then the volume of the hemisphere is calculated as 8 thirds times pi times z cubed. This will result in the total volume calculation of 8 thirds pi z cubed plus 2 pi z cubed equals 14 pi z cubed divided by 3. |
|||||||||||||||||
| 67 | C |
Objective 010 Correct Response: C. The sum of the angles in the circled region of the diagram below must be equal to 360 degrees.  A figure is shown with an octagon at the center. On the outside of the octagon, each of the eight sides forms the base of an isosceles triangle. The angle opposite the base in each triangle is equal to 72 degrees. Angle Z is circled and is indicated as the angle formed between two consecutive isosceles triangles on the outside of the octagon.
A figure is shown with an octagon at the center. On the outside of the octagon, each of the eight sides forms the base of an isosceles triangle. The angle opposite the base in each triangle is equal to 72 degrees. Angle Z is circled and is indicated as the angle formed between two consecutive isosceles triangles on the outside of the octagon.
The measure of one interior angle in a regular polygon can be found using the expression 180 times the quantity n minus 2 all divided by n, where n is the number of sides. For a regular octagon, one interior angle measures 180 times 6 all divided by 8 equals 135 degrees. Since the triangles are isosceles, each base angle 1 half 180 minus 72 equals one half of 108 equals 54 degrees. The measure of angle z can be found by subtracting known angles from 360: 360 minus 135 minus 54 minus 54 equals 117 degrees. Incorrect Response: A. This answer is the result of misinterpreting angle z to be a vertical angle to an interior angle in the octagon. Incorrect Response: B. This answer is the result of misinterpreting angle z to be supplementary to one base angle in the isosceles triangle. Incorrect Response: D. This answer is the result of misinterpreting the measure of angle z to be supplementary to the top angle in the isosceles triangle. |
|||||||||||||||||
| 68 | A |
Objective 011 Correct Response: A. Since C equals 2 pi r, a circle with circumference 16 pi must have a radius of 8. Every point on the circle must be 8 units from the center, (5, 5). If a coordinate point differs from the center by 8 in only the y-variable, then that point is a vertical distance of 8 from the center of the circle. The point (5, negative 3) is 8 units below the point (5, 5), so it will be on the circle. Incorrect Response: B. This point is a distance of 4 units from (5, 5), and it is the result of misinterpreting the radius of the circle to be 4 instead of 8. Incorrect Response: C. This answer is the result of misinterpreting a diagonal distance of 8 in the coordinate plane. This point is units 8 radical 2 away from (5, 5). Incorrect Response: D. This point is a distance of 16 units from (5, 5), and it is the result of misinterpreting the radius of the circle to be 16 instead of 8. |
|||||||||||||||||
| 69 | B |
Objective 011 Correct Response: B. The points (5, 9) and (5, negative 1) form the vertices of one base of the trapezoid since they form a vertical line that is parallel to the y-axis.  A graph with x and y axes with the following 3 points plotted: (negative 1, 7), (5, negative 1), (5, 9)
A graph with x and y axes with the following 3 points plotted: (negative 1, 7), (5, negative 1), (5, 9)
The point (negative 1, 7) forms one vertex of the other base of the trapezoid. Since the second base must also be parallel to the y-axis, the x-value of the missing coordinate point must be negative 1. Since the y-value of the vertex (negative 1, 7) is 2 less than the y-value of (5, 9), use the fact that the trapezoid is isosceles to determine that the final vertex must have a y-value that is two more than (5, negative 1). This leads to the conclusion that the final vertex must be (negative 1, 1). It can be determined that the trapezoid has a height of 6 (the difference between the x-values from one base to another), the short base has a length of 6 (the difference in y-values between the points on the line x = negative 1), and the long base has a length of 10 (the difference in y-values between the points on the line x = 5). Using the formula for the area of a trapezoid, A equals 1 half times the quantity b 1 plus b 2 times h equals 6 plus 10 divided by 2 times 6 equals 8 times 6 equals 48 square units. Incorrect Response: A. This response is likely the result of interpreting the length of the short base to be 4 instead of 6, which would result in the product 7 times 6 for the area using the formula described in the rationale for response B. Incorrect Response: C. This response is the result of misinterpreting the height of the trapezoid to be 7, which would lead to the calculation 8 times 7 for the area of the trapezoid using the formula described in the rationale for response B. Incorrect Response: D. This response is the result of misinterpreting the location of the final coordinate point and misinterpreting the height of the trapezoid. Such errors could result in the product 16 times 4 using the formula described in the rationale for response B. |
|||||||||||||||||
| 70 | A |
Objective 011 Correct Response: A. For angle A B C to be a right angle, the slope of segment A B and the slope of segment B C must have a product of negative 1, or the two slopes must be opposite reciprocals of each other. The slope of segment A B is A 2 minus b 2 divided by A 1 minus b 1 and the slope of segment B C is c 2 minus b 2 divided by c 1 minus b 1. To make the slope of segment B C equal to the slope of segment A B, take the reciprocal of the fraction and multiply the new slope by negative 1 (opposite): c 2 minus b 2 divided by c 1 minus b 1 equals negative 1 times c 1 minus b 1 divided by c 2 minus b 2 equals b 1 minus c 1 divided by c 2 minus b 2 implies A minus b over 2 minus 5 equals 5 minus 9 over c minus b Incorrect Response: B. This response is the result of interpreting the angle as angle C A B. This proportion is derived from using the slopes of A B and A C. Incorrect Response: C. This response is the result of interpreting the angle as angle A C B. This proportion is derived from comparing the slopes of A C and B C. Incorrect Response: D. This response is the result of interpreting the angle as angle A C B. This proportion is derived from comparing the slopes of A C and B C and making an error when applying the opposite. |
|||||||||||||||||
| 71 | D |
Objective 011 Correct Response: D. The coordinates of triangle A B C are A negative 2, 5, B negative 1, 1, and C negative 3, 1. The transformation rule for a reflection over the line y equals x is x y implies y x. The new coordinates of triangle A B C after the reflection are A 5, negative 2, B 1, negative 1, and C 1, negative 3. A 180° rotation counterclockwise is equivalent to a 180 degree rotation clockwise. The transformation rule for a 180 degree rotation is x y implies negative x negative y. The final location of triangle A B C after the rotation is A prime negative 5, 2, B prime negative 1, 1, and C prime negative 1, 3, which is shown in graph D. Incorrect Response: A. This image is the result of reflecting the triangle across the x-axis, reflecting it across the y-axis, and then rotating it 180 degrees about the origin. Incorrect Response: B. This image is the result of reflecting the triangle across the line x = negative 2. Incorrect Response: C. This image is the result of rotating the original triangle 90 degrees counterclockwise about the point (negative 2, 2). |
|||||||||||||||||
| 72 | D |
Objective 011 Correct Response: D. A circle that circumscribes a triangle has a center at the intersection of the perpendicular bisectors of the sides of the triangle. The slope of side segment A B is 8 minus 4 over 8 minus 0 equals one half, making the slope of a perpendicular line to segment A B = negative 2. The midpoint of segment A B equals 8 plus 0 over 2, 8 plus 4 over 2 equals the point 4 6. The equation of the perpendicular bisector of segment A B is y equals negative 2 x plus 14. The slope of side segment B C is 0 minus 4 over 2 minus 0 equals negative 2, making the slope of a perpendicular line to segment B C = 1 half. The midpoint of segment B C equals 2 plus 0 over 2, 0 plus 4 over 2 equals the point 1 2. The equation of the perpendicular bisector of segment B C is y equals 1 half x plus 1 point 5. The intersection of the perpendicular bisectors can be found by solving negative 2 x plus 14 equals 1 half x plus 1 point 5 implies 2 point 5 x equals 12 point 5 x implies x equals 5 and y equals negative 2 times 5 plus 14 equals 4. The radius of the circle is the distance from (5, 4) to one of the vertices of the triangle. Using the vertex (0, 4), r equals the square root of the quantity 5 minus 0 squared plus 4 minus 4 squared equals 5 and the area of the circle is 5 squared times pi equals 25 pi. Incorrect Response: A. This may be the result of interpreting B C to be the diameter of the circle: B C equals the square root of the quantity 4 minus 0 squared plus the quantity 0 minus 2 squared equals radical 20 equals 2 times radical 5. If this is the diameter of the circle, then the area is interpreted as pi times d over 2 squared equals pi times radical 5 squared equals 5 pi. Incorrect Response: B. This answer may be the result of finding the circumference of the circle instead of the area. Incorrect Response: C. This response may be the result of interpreting the segment A B to be the diameter of the circle: A B equals the square root of the quantity 8 minus 0 squared plus the quantity 8 minus 4 squared equals radical 80 equals 4 times radical 5. If this is assumed to be the diameter of the circle, then the area is interpreted as pi times d over 2 squared equals pi times 2 radical 5 squared equals 20 pi. |
|||||||||||||||||
| 73 | C |
Objective 011 Correct Response: C. Consider the median from point A to side B C: The midpoint of B C is 14 plus 4 over 2, 0 plus 12 over 2 equals the point 9 6. Since point A is the origin, the median from A to B C is included in the line 4 equals 2 thirds x implies x equals 6. The center of mass (the intersection of the medians) must be a point on this line. Using substitution with y equals 4 (from the information given in the problem): 4 equals 2 thirds x implies x equals 6. Incorrect Response: A. This response may stem from writing the equation of the line as y equals 9 sixths x then substituting y equals 4 to get x equals 8 thirds. Incorrect Response: B. This response may be the result of using a y-coordinate of 5 instead of 4 in the equation y equals 3 halves x. Incorrect Response: D. This response may be the result of the misconception that the center of mass must be a point on the line x equals 7, since that line is the perpendicular bisector of side A B. |
|||||||||||||||||
| 74 | A |
Objective 011 Correct Response: A. D E equals 2 since E is the midpoint of segment D C. G F equals 2 and angle A G F is a right angle since it is supplemental to angle D G F, which is right for rectangles. segment A F must be the hypotenuse of triangle A G F since it is opposite the right angle, which makes A G equals 2 since it is the other leg in isosceles triangle A G F. A is given as (1, 1), therefore G is (1, 3) and D G equals 5, so the area of the rectangle is 2 times 5 equals 10. Incorrect Response: B. This response may be the result of interpreting point G to be located at (1, 2), which would lead to an area of 2 times 6 for the rectangle. Incorrect Response: C. This answer may be the result of misinterpreting height of the rectangle to be 7 by comparing the y-values between points A and D. Incorrect Response: D. This response may be the result of calculating the area of trapezoid A B C D: 1 half times the quantity 7 plus 3 times 4 equals 20. |
|||||||||||||||||
| 75 | C |
Objective 012 Correct Response: C. A bar graph is most appropriate for this situation because the data are comparing a single measure, the total sales, across six different brands. The total sales for each individual brand could be represented by the height of a bar, and the display would allow for easy visual comparisons of the total sales between each brand. Incorrect Response: A. The most appropriate display for this set of data would be a circle graph or pie chart, since the goal is to show the percentages as parts of a whole. Incorrect Response: B. The most appropriate display for this data set would be a scatter plot. This display would make it easiest to make observations about correlation between the variables. Incorrect Response: D. The most appropriate display to show the change in a single variable over time is a line graph, so a bar graph is less appropriate for this situation than for the situation in response C. |
|||||||||||||||||
| 76 | A |
Objective 012 Correct Response: A. The scores for the three seasons can be converted to a list: 7, 7, 9, 9, 9, 10, 10, 13, 14, 14, 18, 18, 19, 19, 20, 22, 25, 25, 28, 28, 29, 29, 32, 35, 35, 38, 40, 42, 42, 44 The median is the center value when the data set is ordered, which falls between 20 and 22 in this set, so the median is 21. The interquartile range is the difference between the first and third quartile. The first quartile, Q 1, is the median for the lower half of the data, and the third quartile, Q 3, is the median for the upper half of the data. Q 1 equals 13, Q 3 equals 32, so the interquartile range is the difference between those values, 32 minus 13 equals 19. Incorrect Response: B. This answer may be the result of miscalculating the median as 23, perhaps identifying the median between 22 and 25 and rounding or if copying the data into a list, making a copying error. Incorrect Response: C. This answer may be the result of misinterpreting the interquartile range as the range. The interquartile range is the difference between the third quartile and the first quartile, but the range is the difference between the maximum value and the minimum value, in this case, 44 minus 7 equals 37. Incorrect Response: D. This answer may be the result of both errors from responses B and C. The median was determined incorrectly, and the interquartile range was misinterpreted for the range in this response. |
|||||||||||||||||
| 77 | C |
Objective 012 Correct Response: C. The median for the data set is 4, and it remains 4 after 15 is added to the data set at the far right. (Generally, the median is less affected by outliers than the mean.) Incorrect Response: A. The maximum changes from 8 to 15 once the value of 15 is included in the data set. The difference between those values is 7, which represents a more significant change than either the mean or the median. Incorrect Response: B. The mean for the original data set is the sum of all values in the data set divided by 15 equals 52 over 15 which is approximately 3 point 5. After the inclusion of 15, the mean is the sum of all values in the data set plus 15 divided by 16 equals 67 over 16 which is approximately 4 point 2. (Generally, outliers influence the mean more than the median.) Incorrect Response: D. The range for the original data set is 8 (8 minus 0), and it becomes 15 (15 minus 0) once the value of 15 is included in the data set. The change in the range is 7, which is greater than the change in the median and the mean. |
|||||||||||||||||
| 78 | A |
Objective 012 Correct Response: A. For a normal distribution, the data are symmetrical about the mean with approximately 68% of the data existing within one standard deviation from the mean, 95% of the data existing within two standard deviations from the mean, and approximately 99% of the data existing within 3 standard deviations from the mean. The situation in the question is referring to the data that are greater than 1 standard deviation from the mean. Using the symmetry and percentage descriptions from a normal distribution, this implies that approximately 16% of the students have heights that fall in this range: 0 point 1 6 times 50,000 equals 8,000. Incorrect Response: B. This answer could have come from misinterpreting the meaning of 68% of data existing within one standard deviation of the mean and incidentally summing the percentages at both ends of the normal distribution. This number represents the number of students with heights that are at least 173 centimeters and the number of students with heights that are no greater than 163 centimeters: 0 point 1 6 times 2 times 50,000 equals 0 point 3 2 times 50,000. Incorrect Response: C. This value represents the number of students who are within 1 standard deviation from the mean. These students have heights between 163 centimeters and 173 centimeters: 0 point 6 8 times 50,000 equals 34,000. Incorrect Response: D. This response likely stems from a misinterpretation of the data that are specified in the question. This value represents the number of students who are no taller than 173 centimeters. It is the complement of the data set from what is specified in the question: 0 point 8 4 times 50,000 equals 42,000. |
|||||||||||||||||
| 79 | C |
Objective 012 Correct Response: C. Without knowing the demographics of the communications collected, this is a potential concern that could misrepresent the constituency. There is not enough information provided to know that the sample is random, so there is no way to guarantee that it is representative of the entire constituency. (The bias that can exist in a survey where the participants are volunteers is the same source of bias that may exist in this context.) Incorrect Response: A. Generally, a larger sample is a better representation than a smaller sample, but only if the sample is random. There is no guarantee that the sample is random in this situation, so the results may be disproportionately impacted by a specific group, which could make the data an invalid representation of all constituents. Incorrect Response: B. Even though access promotes broad participation, it does not ensure that an ideologically diverse group of people exercise the right to vote. The constituents who did vote may have been part of a specific, highly motivated group, which could have skewed the data. Access does not ensure that the sample is random. Incorrect Response: D. The outcome of the bill should be the result of the opinions of the constituents, so this is not an accurate assessment of potential bias in the results. |
|||||||||||||||||
| 80 | C |
Objective 013 Correct Response: C. The data can be represented with a Venn diagram, where C = the set of students who saw the comedy movie and A = the set of students who saw the animated movie. The intersection of both sets, which is the percentage of students who saw both movies, is 14%. 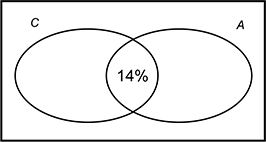 A venn diagram with circles labeled C and A that are partially overlapping. The overlapping region is labeled as 14 percent.
A venn diagram with circles labeled C and A that are partially overlapping. The overlapping region is labeled as 14 percent.
Since 55% of students saw the comedy movie, and this includes the 14% who saw both, then 55 minus 14 or 41% of students saw only the comedy movie. Likewise, the 28% of students who saw the animated movie includes the 14% who saw both. So, 28 minus 14 or 14% saw only the animated movie. 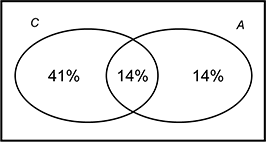 A venn diagram with circles labeled C and A that are partially overlapping. The overlapping region is labeled 14 percent, the region that represents only C is labeled 41 percent, and the region that represents only A is labeled as 14 percent.
A venn diagram with circles labeled C and A that are partially overlapping. The overlapping region is labeled 14 percent, the region that represents only C is labeled 41 percent, and the region that represents only A is labeled as 14 percent.
Since the Venn Diagram includes 100% of the students, the percent of students who saw neither movie must be 100 minus the sum of the percentages within the sets or 100 minus the quantity 41 plus 14 plus 14 equals 100 minus 69 equals 31. 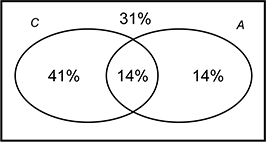 A venn diagram with circles labeled C and A that are partially overlapping. The overlapping region is labeled 14 percent, the region that represents only C is labeled 41 percent, and the region that represents only A is labeled as 14 percent. The region outside of both circles is labeled as 31 percent.
A venn diagram with circles labeled C and A that are partially overlapping. The overlapping region is labeled 14 percent, the region that represents only C is labeled 41 percent, and the region that represents only A is labeled as 14 percent. The region outside of both circles is labeled as 31 percent.
Incorrect Response: A. This response may be the result of adding the 55% and 28% in the question without considering how the overlap affects those percentages. Then, 100 minus 87 produces 13%. Incorrect Response: B. This response may be the difference between the percentage of students who saw neither movie and the percentage of students who saw both movies, or 31 minus 14 equals 17 percent. Incorrect Response: D. This response is the percentage of students who saw only the comedy movie. |
|||||||||||||||||
| 81 | B |
Objective 013 Correct Response: B. Probabilities can be assigned to each of the first three branches of the tree diagram using the fact that there are 12 markers total in the box. Information regarding what fraction of each marker is dry can be used to assign probabilities to the second set of branches.  The tree diagram is shown from the question with probabilities labeling the branches. On the first level, red, green, and blue are labeled 1 sixth, 1 third, and 1 half, respectively. On the second level. Which represents dry or not dry for each color, the probabilities are as follows:
The tree diagram is shown from the question with probabilities labeling the branches. On the first level, red, green, and blue are labeled 1 sixth, 1 third, and 1 half, respectively. On the second level. Which represents dry or not dry for each color, the probabilities are as follows:
Red dry 1 half Green dry 1 fourth Blue dry 1 half To the right of each pair of branches at the final level of the diagram are the following probabilities: 1 twelfth, 1 twelfth, 1 fourth. The product of the probabilities along the branches in each path shows the probability that a given marker meets both criteria (e.g., is green and dry = 1 twelfth). To find the probability that a randomly selected marker is dry, we must add the probabilities for each path that represents a dry marker. The sum of the possibilities for drawing a dry red, dry green, or dry blue marker is 1 twelfth plus 1 twelfth plus 1 fourth equals 5 twelfths. Incorrect Response: A. This result could be due to a misinterpretation of the meaning of the first three branches in the tree diagram. Incorrect Response: C. This result could be a misinterpretation of the probability specified in the question. This is the probability that a randomly selected marker will be blue. Incorrect Response: D. This result could be a calculation of the complement for the probability specified in the question. This is the probability that a randomly selected marker is not dry. |
|||||||||||||||||
| 82 | A |
Objective 013 Correct Response: A. The probability of selecting the first red number cube from the bag is 2 thirds, and the probability of selecting a second red number cube is 1 half, since the number cubes are drawn without replacement. The probability of selecting two red number cubes from the bag is then 2 thirds times 1 half equals 1 third. Once the two red number cubes are selected, there are 2 possible ways to roll a resulting sum of 3: (1, 2) or (2, 1). There are 6 times 6 or 36 total possibilities for rolling two number cubes, so the probability of rolling a sum of 3 is 2 thirty-sixths equals 1 eighteenth. The probability of selecting two red dice and rolling a sum of three is 1 third times 1 eighteenth equals 1 fifty-fourth. Incorrect Response: B. This answer may be the result of interpreting the probability of choosing two red number cubes as 1 half, and correctly calculating the probability of rolling a sum of three. This would lead to calculating the probability of selecting two red number cubes and rolling a sum of three as 1 half times 2 thirty-sixths equals 1 thirty-sixth. Incorrect Response: C. This answer may be the result of errors related to the formation of the sample space, or it may be the result of incorrectly adding probabilities for different events in the problem. Incorrect Response: D. This answer may be the result of calculating the probability of rolling a sum of 3 on two number cubes without considering the probability that the two chosen number cubes are red 2 thirty-sixths equals 1 eighteenth. |
|||||||||||||||||
| 83 | C |
Objective 013 Correct Response: C. If we define the number of green grapes originally in the bag to be x, then the number of green grapes in the bag after 5 are removed is equal to x minus 5 and the total number of grapes in the bag is x minus 5 plus 25 equals x plus 20. We can then say that x minus 5 divided by x plus 20 is less than 0.25 implies x minus 5 is less than 0.25 times the quantity x plus 20 implies x minus 5 is less than 0.25 x plus 5 implies 0.75 x is less than 10 implies that x is less than 13 point 3 repeating. Since x must be less than 13 point 3 repeating, and we are assuming there are only whole grapes in the bag, the greatest number of green grapes possible at the start is 13. This means that there could have been as many as 13 plus 25 equals 38 grapes in the bag originally. Incorrect Response: A. This response is the result of finding the correct answer, 38, but then adding the value of 5 back to it. The solution process outlined in the correct response finds the total number of grapes before 5 are removed, so adding 5 to that value is unnecessary. Incorrect Response: B. The same solution process from the correct response is used, but the result is rounded up to the nearest whole value, which could lead to the answer of 14 plus 25 or 39. Incorrect Response: D. This may be the result of solving the original inequality, which leads to an answer of x is less than 6 point 6 repeating, which could lead to the answer 25 plus 6 equals 31. |
|||||||||||||||||
| 84 | B |
Objective 013 Correct Response: B. There is a one-to-one correspondence between the sample spaces for the range of numbers from 1through 26 and the set of letters from Ato Z . This simulation samples from each set in the same manner, and each of the 100 sets can be easily compared to the criteria to check for at least one vowel. Incorrect Response: A. The question does not specify that each of the random five letter samplings must be words, so this simulation does not accurately describe the scenario. Incorrect Response: C. This simulation assumes that there is an equal probability of choosing a vowel or a consonant when randomly choosing a letter of the alphabet, which is not true. Incorrect Response: D. The simulation described does not allow for the repetition of letters within a five-letter sample, which is not consistent with the scenario in the question. Additionally, the simulation involves drawing samples until "only one vowel" is drawn, rather than at least one vowel. |
|||||||||||||||||
| 85 | B |
Objective 013 Correct Response: B. To find the probability of an alternating color pattern, look at the probability for creating the pattern in each position on the wire, where flags are chosen without replacement. Consider the scenario shown below. 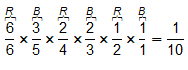 The product of six fractions is shown, with labels that alternate R, B, R, B, R, B. 6 over 6 times 3 fifths times 2 fourths times 2 thirds times 1 half times 1 over 1 equals 1 tenth.
The product of six fractions is shown, with labels that alternate R, B, R, B, R, B. 6 over 6 times 3 fifths times 2 fourths times 2 thirds times 1 half times 1 over 1 equals 1 tenth.
The starting color is arbitrary, so the probability of selecting either a red or a blue flag for that position is 6 over 6 equals 1. For the next position, the flag must be the other color from what filled the previous position, and there are 3 of those flags out of 5. For position 3, there are 4 remaining flags, 2 of which can satisfy the pattern, so the probability is 2 fourths. This logic leads to a probability of 2 thirds for the fourth position, 1 half for the fifth position, and only one flag remaining for the sixth position, which has a probability of 1. The product of the probabilities is 1 tenth. Incorrect Response: A. This response may be the result of reaching an answer of 1 tenth using a similar strategy shown in the rationale for response B, but then multiplying by 1 half to account for the fact that two different colors can start the pattern. As described in B, the solution process already considers both options. Incorrect Response: C. This answer may be the result of interpreting the probability as a product 1 half times 1 half, which does not consider all six positions on the wire or the fact that the flags fill positions "without replacement." Incorrect Response: D. This answer may stem from misunderstanding that the flags are drawn to fill positions "without replacement." If there are always 3 red and 3 blue to choose from, the probability of filling any single position with one color or the other is 1 half. |
|||||||||||||||||
| Total Correct: | Review your results against the test objectives. | ||||||||||||||||||
Open Responses, Sample Responses, and Analyses
| Question Number |
Your Response Read about how your responses are scored and how to evaluate your practice responses |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 86 |
Open Response Item Assignment #1 For each assignment, you may type your written response on the assigned topic in the box provided. Note: The actual test allows you to handwrite your responses on separate response sheets to be scanned for upload to the test. For this practice test, you may handwrite each response on 1–2 sheets of paper. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Sample Weak Response |
First Sample Weak Response to Open-Response Item Assignment #1 Prerequisite Skills for this standard: The student must be able to find the ratio between two quantities. The student must be able to work with fractions. Representations: Create a table
Activity: Pass out a large piece of paper to each student. Have them fold and record results repeatedly on a separate piece of paper. Make predictions for the eighth fold. Alignment: The problem does not align with the standard since number of folds to number of boxes is an exponential relationship not linear. The actual answer to the problem is 2n2 to the power of n where n is the number of folds |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Weak Response Analysis |
Analysis of First Weak Response to Open-Response Item Assignment #1 Purpose: The response does address Part 1 and focuses on the objective given with two prerequisites that are reasonable; however, the response does not explain their relevance to the objective. In Part 2, the response focuses on the given problem instead of modeling the mathematics given in the standard and does not explain why each representation used is appropriate. In Part 3, the response does recognize that the given problem does not align with the standard and gives an acceptable explanation of why it does not align. Subject Matter Knowledge: The response to Part 1 is minimal with the number of prerequisite skills needed to achieve this objective and does not address why the two prerequisite skills given are appropriate. This objective has many prerequisite skills needed after fractions that should be addressed. For example, conceptual understanding of proportional reasoning, meaning of rates, the meaning of percentage, and simple rate and percentage problems before developing multi-step problem solving. In Part 2, the response never creates representations that model the standard given, but instead uses the paper-folding problem, which does not address the standard appropriately. In Part 3, the response does show an understanding that the given problem is not a multi-step problem using ratios, rates, or percentages. The response gives an acceptable explanation of why this problem does not align with the standard. Support: In general, the response lacks support for the statements and work given. Part 1 gives minimal prerequisites and does not explain why they are appropriate. Part 2 is not a valid response for modeling the standard. Since the problem given does not align with the standard, it should not be used to create two or three representations to model the standard. Part 3 does correctly respond to whether it aligns to the standard and presents an explanation of why it does not align. Rationale: The response reflects a limited, poorly reasoned understanding of the topic. The response gives few prerequisite skills and does not explain why they are needed. The response does show two ways of representing the given problem but does not give multiple ways of representing the skills needed for the standard nor why the representations are beneficial and appropriate. The response does reason why the problem given is inappropriate for the standard but is more focused on the problem than the standard. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Sample Weak Response |
Second Sample Weak Response to Open-Response Item Assignment #1 Part 1: The prerequisite skills needed to do this standard are to be able to change a fraction to a percent and to be able to set up and solve a proportional relationship. Part 2: Problem: A student takes an exam and gets 17 out of 20 questions correctly solved. What grade did the student get on the exam? Method 1: Make a ratio table-
Method 2: Write a proportion: 17 over 20 = question mark over 100 Part 3: The problem given does not align well with the standard though it does mention ratios which is why a new problem was made. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Weak Response Analysis |
Analysis of Second Weak Response to Open-Response Item Assignment #1 Purpose: The purpose of the assignment is partially achieved. Part 1 gives two prerequisite skills that are appropriate for this standard. Part 2 of the response gives a problem situation and two representations to model mathematics in the standard but does not explain why they are appropriate. Part 3 does make a statement about the alignment of the problem given. Subject Matter Knowledge: Part 1 of the response shows some understanding of the prerequisite skills needed to successfully do this standard but does not explain why they were chosen or why they are important. Part 2 gives a new situation that does align with the standard and gives two representations that could be helpful. Part 3 states correctly that the original problem does not align with the standard. Support: Part 1 identifies two prerequisite skills but there is no explanation of their relevance to the standard. Part 2 provides two possible representations that could work, but there is no explanation of how to use them or why they would contribute to increasing student understanding of the topic. Part 3 correctly states that it is not aligned, but there is no explanation of the reasoning for arriving at that conclusion Rationale: There is a limited understanding of subject matter knowledge. The candidate offers possible correct responses but none of them are supported with any details or explanations. The "why" or the "how" is never addressed. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Sample Strong Response |
First Sample Strong Response to Open-Response Item Assignment #1 Prerequisite skills: 1) What ratio means, how ratios are used, how ratios can create proportions to explain relationships. These are needed in or to be able to understand and use rates, percentages, and word problems. 2) The concept of rate when compared to 1 unit, e.g., miles per 1 hour etc. This is needed in standard in order to do word problems that deal with different forms of rate: speed, interest rate, growth. 3) The meaning of percent as it relates to ratios, rates, and proportions. The concepts of ratios, rates, proportions, and percent are all connected, and the relationship needs to be understood in order to understand how to solve equations and problems that use them. 4) Perform calculations between fractions, decimals, proportions, and percent. In order to do multi-step problems related to this standard the student needs to be able to easily do these calculations. This standard requires students to draw on this prior knowledge as they learn to recognize and solve multi-step problems using a proportion and a percentage. Using the following problem, I'll create appropriate representations to model the math in the standard: Jill sold 10 boxes of cookies in 1 day. Her goal is to sell a total of 50 boxes of cookies. If Jill continues to sell 10 boxes per day: How many days will it take to reach her goal? What percentage of her goal did she sell on Day 1? 1. Table illustrating cookie sales.
A table clearly organizes data so students can see a pattern between boxes and days. Rate can be discussed with the students easily with the students using the table above relating it to a ratio table which they have seen before. Then have students represent this in a bar graph so they can understand the same information visually and see that the growth is increasing at a constant rate of 10 boxes of cookies per day and see where that is found in the table, relating the two representations. 2. Bar graph (see picture)
3. Numerical representation. Ask students, "What percentage of her goal did Jill sell on her first day?" 10 of 50 sold on day 1 which is 20 of 100 which is 20% OR Ten fiftieths equals 20 hundredths equals 20 percent. This shows the connections among ratios, percentages, and proportions. This multi-step problem demonstrates the standard. To solve it, the student can develop a ratio of cookies sold to days; construct a proportion to determine the total number of days needed to reach the goal; and calculate the daily percentage rate of sales. The paper folding example doesn't align with the standard because the relationship between the folds and boxes created is not proportional but an exponential relationship of 2n2 to the power of n. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Strong Response Analysis |
Analysis of First Strong Response to Open-Response Item Assignment #1 Purpose: The purpose is fully achieved. This response addresses all three parts of the assignment. The prerequisite skills and concepts are clearly stated, and their relevance is explained. The candidate identifies that the Problem Situation does not align with the standard and creates a relevant problem about cookie sales to model representations of ratios, percentages, and proportions, explaining why each representation is appropriate. Subject Matter Knowledge: There is substantial application of subject matter knowledge. For example, the candidate provides three different and appropriate ways to model the mathematics required in the standard. By using a table, the candidate shows how to organize the data to solve the problem. By selecting a bar graph, the candidate illustrates the relationship between the two variables pictorially. Finally, the candidate demonstrates the relationship between ratios, proportions, rate, and percent numerically as a multi-level problem. Additionally, the candidate realizes the problem given does not align with the standard and explains why. Support: The candidate gives high-quality, relevant examples to answer all components of the question. For instance, the candidate lists multiple prerequisite skills for the standard and explains their relevance. The cookie problem shows how ratios, percent, and proportions are related to each other with the specific and distinct examples of the bar graph, table, and numerical representation, all of which emphasize different approaches or types of understanding. The model shows a multi-step process to find solutions. Lastly, the candidate reaches a sound conclusion about the alignment of the original problem to the objective and defends why it does not align Rationale: The candidate shows a comprehensive understanding of the topic by identifying the prior skills required for the standard (and their relevance to the standard), how to appropriately represent the standard in multiple ways—as a table, as a bar graph, and numerically—and why these representations are beneficial and appropriate. Additionally, the candidate reasons why the original situation is inappropriate for the standard. At each step, the candidate logically explains their reasoning, resulting in a sound argument. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Sample Strong Response |
Second Sample Strong Response to Open-Response Item Assignment #1 Part 1. Prerequisite Skills: Conceptual understanding of ratios, rates, percentages and proportions and ways to represent them. Equivalent ratios are multiples of that "unit." Students must know that a "rate" is a type of ratio relating something to one. Students must be comfortable with converting ratios, fractions and decimals to percent and vice versa. All these skills help students develop the multiplicative thinking necessary to understand proportional relationships. Part 3. The problem given doesn't align well with the standard. Though answers are given using the ratio of folds to number of squares, the focus of the problem is finding a pattern using powers of 2, which is an exponential relationship. Part 2. To Model Standard: Problem: An animal shelter holds an adoption event to help get homes for their dogs and cats. They notice that two dogs are adopted for every three cats adopted. At the end of the day, 21 cats were adopted. How many dogs were adopted that day? What percent of the dogs and cats adopted that day were cats? Representation 1 - Physical: Give students strips of paper with five squares drawn on each of the strips. On each strip, label two squares D for dog and three C for cat. What is the ratio of dogs to cats? What is the ratio if you use 3 strips? If you use 7 strips? This is a visual/conceptual way to understand ratios and see equivalent ratios. Representation 2 – Numerical: Next, make a table with five columns: number of strips, number of dogs, number of cats, number of cats and dogs, percent of cats adopted. Ask students to use at least ten strips and complete the table. This will organize their information and visually show the relationships between multiple ratios in developing proportions and percent. The students will see that the dogs to cats ratio, the cat to both dogs and cats ratio can be expressed many ways using multiple sets of the original ratio and that the percent of cats to both dogs and cats does not change because the multiple sets are all the same ratio of animals. If you have 10 sets of 2 dogs, you have 10 sets of 3 cats. The ratio is still 2 to 3. See table below. Representation 3 – Verbal: Ask questions like 1 strip gives them how many animals? 9 cats give them how many dogs? Show a proportion that would give a solution. By asking these questions, the student is challenged to discover a way to make a proportion and develop a solution (see sample below). Example for Representation 2. Table showing 2 dogs for every 3 cats are adopted
Example for Representation 3. Proportion: 3 cats over 2 dogs = 9 cats over x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Strong Response Analysis |
Analysis of Second Strong Response to Open-Response Item Assignment #1 Purpose: The purpose is fully achieved because all bullets are addressed well. The response addresses the standard given with multiple prerequisites, including their relevance to the objective. The response gives an example that demonstrates a physical way to understand (using the strips of paper), a numerical way of demonstrating the situation (using a table), and then verbally reinforces the relationships in the problem written as ratios and using those as a proportion to find an answer. The third bullet is addressed fully by stating that the sample problem given does not align with the standard and explaining why it does not align. Subject Matter Knowledge: The response shows a clear and accurate understanding of what these three topics (ratios, proportions, percent) are conceptually. It demonstrates multiple ways to improve and reinforce students' understanding of what a ratio is, how multiples of that ratio make a proportion, and how a table helps to find patterns and organize information as well as leads to an equation (proportion) that can be solved using the same kind of thinking. For example, by using strips of paper labeling the relationship between cats and dogs, the student can visually and concretely understand that ratio. Support: The response provides multiple prerequisites and explains the relevance to the objective given. For each of the representations, relevant and detailed examples are shown to support the statement. For example, in creating the table, the student must demonstrate multiple ways to represent ratios, and use them to solve proportions and calculate percentages. There is a multi-step process built into the problem. The response states that the sample does not align and explains why. Rationale: The response demonstrates a sound argument and high degree of understanding of the topic. It is written in a way that can be easily followed and understood. The prerequisites are clearly stated; the subject matter knowledge is appropriate and accurate for the standard; the support is sound; and the critique of the sample problem states a valid response and gives an explanation that is supported. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 |
Open-Response Item Assignment #2 For each assignment, you may type your written response on the assigned topic in the box provided. Note: The actual test allows you to handwrite your responses on separate response sheets to be scanned for upload to the test. For this practice test, you may handwrite each response on 1–2 sheets of paper. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Sample Weak Response |
First Sample Weak Response to Open-Response Item Assignment #2 1. See my tree below. 2. To make one device, 1st stage has an 80% chance of being good or 4 fifths. If it makes the 2nd stage, it has a 75% chance of being good or 3 fourths. So good ones are 4 fifths times 3 fourths equals 3 fifths chance of being created. Therefore, produce 5 devices and you should get 3 good devices. 3. Produce your own 3 devices – you make more profit. 4. If the factory burns down, then you have to buy Stage 1 and Stage 2 parts from the supplier and make less profit.
The first vertex, labeled 1 device, has two branches. The bottom branch is labeled Stage 1, 20 percent defective, discard, and this branch is terminal. The top branch is labeled Stage 1, 80 percent usable, and two branches extend from it. The top branch is labeled Stage 2, 75 percent usable, and the bottom branch is labeled stage 2, 25 percent defective, discard. Both of these second-level branches are terminal. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Weak Response Analysis |
Analysis of First Weak Response to Open-Response Item Assignment #2 Purpose: The purpose of the assignment is limited, although each part is partially addressed. In Part 1, the tree diagram does demonstrate an understanding of the situation but does not include all pertinent information. Part 2 is adequate, but Part 3 just provides an answer with no reasoning. Part 4 names only one influence. Subject Matter Knowledge: The response demonstrates a limited understanding of the topic. In Part 1, there is knowledge of how to draw a tree diagram and gives basic information pertaining to this situation. In Part 2, the response demonstrates an understanding of how to use probability to find the number of usable devices and in Part 3 arrives at a conclusion. Part 4 identifies an influence, though an unlikely one. Support: The support for this response is limited. Part 1 provides a tree diagram but would be improved by including information about the cost at each stage or the loss at each stage. Part 2 shows work but does not explain why this process is being used or why the conclusion reached is valid. Part 3 gives an unsubstantiated conclusion. No work is shown to compare the cost of the company making their own versus buying devices from another company. The response ignores all information about cost, profit, and losses, which are needed to explain their decision. Part 4 identifies one influence when the prompt asks for "influences." An adequate response would include at least two and more likely three influences with an explanation of what effect each would have on the recommendation. Rationale: The response reflects a limited understanding of the topic and much of the reasoning is lacking. Reasons and recommendations are given without sufficient justification. The response shows some understanding of the topic, but there is not enough support or explanation for how answers and conclusions are derived. If any analysis was done, it is not shown. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Sample Weak Response |
Second Sample Weak Response to Open-Response Item Assignment #2 1. I chose to change the 80%, 20%, 75%, and 25% into reduced fractions and used that information to create my production tree (see below). 2. From the tree diagram and the denominator of the fractions for Stage 1 it appears that if you start by making 5 devices, one of them will not pass inspection at end of Stage 1 leaving only 4 going onto Stage 2. At the end of Stage 2 one of the 4 will not pass inspection leaving only 3 good ones to be sold. You need to make 5 to get 3 good ones. 3. Should the company outsource production if they only want 3 units? It will cost 9,000 dollars in total for the 3 from the outside company. The manufacturing company charges 3,500 dollars for each good unit so only makes 500 dollars per unit. Total of 1,500 dollars profit If first 3 units are perfect, selling price of 3,500 dollars minus production cost 1,200 dollars is 2,500 dollars profit each unit. Manufacture the units yourself! Better profit. 4. If the company could no longer get some of raw materials needed for production at the present price, the costs at Stage 1 and/or Stage 2 would increase which cuts into profits. The only person who can run the Stage 2 machinery had a medical emergency and will be out several weeks until another person can be trained on the equipment.
The first vertex is labeled Start production of 5. One branch labeled Stage 1 extends from this vertex. The top branch of the second label is labeled 1 bad. It is a terminal branch. The bottom branch of the second level is labeled 4 go to Stage 2. Two branches extend from the end of its arrowhead. The top branch is labeled 1 bad. It is a terminal branch. The bottom branch is labeled 3 ready to sell, and this is a terminal branch. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Weak Response Analysis |
Analysis of Second Weak Response to Open-Response Item Assignment #2 Purpose: All parts of the prompt are addressed. Part 1 includes a tree diagram but does not answer with a tree for one device only. Part 2 has a correct answer but there is no justification for the numbers shown. Part 3 addresses the profit for outsourcing the device but incorrectly responds to the profit if made in-house. Part 4 identifies two influences and some justification for each. Subject Matter Knowledge: The response reflects a limited and possibly inaccurate application of the subject matter. Part 1 misinterprets the wording of the question by making a tree for five devices instead one device. Part 2 uses the tree to arrive at the conclusion that five are needed, but the analysis is not clearly shown. Part 3 shows a partial understanding of the situation. The response accurately finds the profit if the devices are outsourced. The response does not analyze profits and losses when produced in-house. An assumption is made that the first three devices made were acceptable for sale, giving maximum profit, and ignoring the probability that at least two in every five will be defective, causing a reduction in profit. Part 4 names two reasonable influences and justifies why they could affect the recommendation. Support: The response shows very limited support. In Part 1, the diagram lacks pertinent information about cost or loss in each branch of the tree and has little explanation of how the numbers used in the diagram were found. It mentions changing percentages to fractions but does not show it or justify why it was done. Part 2 uses the numbers from the tree but again never clearly shows how they were found or why they were chosen. Part 3 shows good support for the profit if the device is outsourced but uses faulty reasoning in analyzing the profit if the company decides to make the device in-house. The cost of making the two possible defective devices is ignored and the effects on the total profit. Part 4 names only two influences but does explain why the recommendation might change. Rationale: The response shows some understanding of the topic but ignores the wording of Part 1 of the prompt, which clearly states to make a tree for one device. Throughout this response, clarifying detail is missing, making the response difficult to follow and understand. The thinking used to arrive at conclusions is not shown, and without it, there is no way to know if the reasoning is correct. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Sample Strong Response |
First Sample Strong Response to Open-Response Item Assignment #2 1. (See tree diagram.) Summarize net profit/loss: 3 fourths of 0.8 or Three fourths of four fifths pass final inspection or 3 fourths times 4 fifths equals 3 fifths can be sold at 3,500 dollars. 2 fifths of devices are thrown away: 1 fifth times 0 point 2 at stage 1 for a 700 dollars loss per device and 1 fifth left paren 1 fourth of 4 fifths right paren at stage 2 for a 1,200 dollars loss per device.
A note at the top of the diagram says each Initially each device costs 700 dollars. The first vertex is labeled $700 per device, and two branches extend from this vertex to the first level of the tree, labeled stage 1. A terminal branch labeled zero point 2 extends downward and right. Its vertex is labeled Fail, lose that 700 dollars. An arrow points from that vertex label to a note that says throw away. The other first level branch extends downward and left, and it is labeled zero point 8. Its node is labeled Pass, need 500 dollars more each to finish, 700 plus 500, total cost after this step. Two branches extend from this vertex into the second level of the tree, labeled stage 2. One branch is labeled 0 point 75, and the label at its terminal vertex reads pass, each cost 1200 dollars. The other is labeled 0 point 25 and the label at its terminal vertex reads fail, lose that 1200 dollars. An arrow points from that label to a note that says throw away. 2. 3 fourths of 0.8 pass stage 2 which is 3 fourths of 4 fifths which is the same as 3 fourths times 4 fifths equals 3 fifths pass so 3 out of 5 devices made pass inspection and can be sold. So at least 5 attempts to get 3 to sell. 3. Three devices passing inspection costs 3 times 1,200 dollars for them and 700 dollars lost at stage 1 for one device and 1,200 dollars lost at stage 2 for another device. 3600 + 700 + 1200 = 5,500 dollars total to make 3 good devices that can be sold. If the other company charges 9000 dollars for 3 devices, they should make the devices for themselves and save 9000 minus 5500 equals 3,500 dollars. If they sell each device for 3,500 dollars, 3 would make 10,500 dollars minus 5500 equals 5000 dollars profit on 3 devices. 4. Things that could influence the prediction/outcome would include upfront costs (buy equipment, train workers, supply chain issues, change in costs of materials) or machine malfunctioning so expected percentages are not as expected. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| First Strong Response Analysis |
Analysis of First Strong Response to Open-Response Item Assignment #2 Purpose: The purpose of the assignment is fully achieved. All parts are addressed completely with work shown and thinking explained. In Part 1, a tree diagram shows relevant information at each branch. In Part 2, the ratios are provided, and the steps are clear and easy to follow for the processes needed for production. The thinking for arriving at the conclusion that five are needed in order to have three to sell is explained. The work shown and explained in the analysis of Part 3 is complete. Many influences are identified in Part 4. Subject Matter Knowledge: There is substantial and accurate application of knowledge. In Part 1, the tree diagram is clear and concise, providing all the information needed. The work demonstrated in Parts 2 and 3 shows understanding of the situation and step-by-step calculations to arrive at the solutions, with explanation of the steps used to make the appropriate decisions. In Part 4, the influences given are appropriate and could affect the manufacturing process. Support: There is high-quality support for each part of the response with step-by-step work shown and reasons given for each step so that it is easy to understand how each decision was made. Part 1 shows a well-drawn tree with each branch labeled appropriately with manufacturing cost or possible loss. In Part 2, the work needed is clearly shown and explained to arrive at the conclusion of five devices needed. In Part 3, step-by-step analysis of outsourcing as opposed to in-house production leads to a well-justified conclusion. Part 4 lists many influences that can affect the recommendation given. Rationale: The response is an ably reasoned analysis of the problem. The steps shown and reasoning used in each part make it easy to follow and understand why they are needed. The response integrates all four parts of the problem into a well-explained analysis of the situation. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Sample Strong Response |
Second Sample Strong Response to Open-Response Item Assignment #2 See tree diagram below. The probability of creating a successful device is 4 fifths times 3 fourths or 3 fifths left paren 60 percent right paren. Therefore, make the following equation with x standing for the number of devices which need to be produced, 3 fifths probability of success and 3 the number of good devices requested: 3 fifths x equals 3 Solve for x. x equals 3 times 5 thirds which makes x = 5. It should only take 5 tries to get 3 good devices according to theorical probability. To determine whether the company should outsource manufacturing, calculate expected profit of in-house vs outsourced manufacturing. If the company wants to produce 3 sellable devices, they should produce 5 devices. 3 of them will be sellable and cost the company 1,200 dollars each to produce. One will fail quality testing at the end of stage 1, costing the company 700 dollars. One will pass stage 1 testing but fail quality testing after stage 2, costing the company 1,200 dollars. So, the 5 devices' total cost is 3 times 1,200 dollars plus 1 times 700 dollars plus 1 times 1200 dollars. Therefore, total cost equals 3600 plus 700 plus 1200 equals 5,500 dollars. The company will sell the 3 good ones for 3,500 dollars each, for a total of 10,500 dollars. Their profit is total sales minus manufacturing costs – in this case, 10,500 minus 5,500 equals 5,000 dollars. If the company outsources manufacturing, their cost is 9,000 dollars. They still have the same total sales income, so 10,500 minus 9,000 equals 1,500 dollars profit. The company should manufacture its own devices since it will make more profit by producing 5 devices and possibly having 2 that are unusable. Influences that could cause variations: the manufacturing equipment requires repair and is shut down for several days; the materials needed to create the device are not available, but the external manufacturer has them; or employee attendance is not reliable, which means the machine needs to be stopped until they return to work.
The initial node is labeled single device. One terminal branch, labeled bad, 20 percent, one-fifth chance, extends from the initial node. A note appears at the arrowhead of this branch. It reads branch 2, 700 dollars cost, 700 loss. The other first-level branch is labeled good, 80 percent, four-fifths chance. It extends to a node that is labeled 700 cost. Two terminal branches extend outward from this node. The first second-level branch is labeled bad, 25 percent, one-fourth chance. A note appears at the arrowhead of this branch. It reads branch 3, 500 dollars cost, 1200 loss. The other second-level branch is labeled good, 75 percent, three fourths chance. It ends at the following note: branch 1, 500 dollars cost, profit 3500 dollars minus 1200 dollars equals 2300 dollars. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Second Strong Response Analysis |
Analysis of Second Strong Response to Open-Response Item Assignment #2 Purpose: The purpose of the assignment is fully achieved. In Part 1, a tree diagram was created and labeled with all pertinent information. Part 2 shows step-by-step work to arrive at the answers needed, including explanations for what was done and why it needed to be done. Part 3 thoroughly analyzes the cost of production versus outsourcing the three devices. Work is shown and explained in a way that leads to the decision. In Part 4, several influences are given that could change the recommendations. Subject Matter Knowledge: The response shows a clear understanding of the topic. Each part is ably reasoned showing the thinking involved and reasoning used. In Part 1, a complete tree diagram is created. Work shown to arrive at answers in Parts 2 and 3 is clear and easy to follow and explained fully. Influences given are appropriate and show an understanding of the real-world situation. Support: All parts of this response are supported. Each part responds to the question, showing step-by-step work and explanation for why the steps were included and why the conclusions were drawn. Rationale: This is an ably reasoned, comprehensive response to the prompt. The response shows good understanding of the topic, giving reasons for the calculations and providing analysis. The response is easy to follow and supports and defends the analysis well. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Review the Performance Characteristics and Score Scale for Written Performance Assignments. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multiple Choice Question
Practice Test Evaluation Chart
In the evaluation chart that follows, the multiple-choice questions are arranged in numerical order and by test objective. Check your responses against the correct responses provided to determine how many questions within each objective you answered correctly.
Subarea 1 : Number System and Quantity
Objective 0001: Apply the structure and properties of number systems.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 1 | C | |
| 2 | B | |
| 3 | D | |
| 4 | B | |
| 5 | D | |
| 6 | D | |
| 7 | C | |
| 8 | B | |
| 9 | C | |
| 10 | A |
out of 10
Objective 0002: Use rational numbers, ratios, and proportional relationships.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 11 | B | |
| 12 | D | |
| 13 | C | |
| 14 | C | |
| 15 | C | |
| 16 | B | |
| 17 | B | |
| 18 | C | |
| 19 | B | |
| 20 | C | |
| 21 | B | |
| 22 | A |
out of 12
Subarea 1 (Objectives 0001–0002) Total out of 22
Subarea 2 : Algebra, Functions, and Modeling
Objective 0003: Use patterns to model and solve problems.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 23 | C | |
| 24 | B | |
| 25 | B | |
| 26 | A | |
| 27 | D | |
| 28 | D | |
| 29 | B | |
| 30 | B |
out of 8
Objective 0004: Apply algebraic techniques to expressions and equations.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 31 | D | |
| 32 | C | |
| 33 | B | |
| 34 | D | |
| 35 | D |
out of 5
Objective 0005: Demonstrate knowledge of relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 36 | A | |
| 37 | D | |
| 38 | D | |
| 39 | C | |
| 40 | A |
out of 5
Objective 0006: Apply the properties of linear relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 41 | B | |
| 42 | D | |
| 43 | C | |
| 44 | C | |
| 45 | B | |
| 46 | A | |
| 47 | C | |
| 48 | B | |
| 49 | C |
out of 9
Objective 0007: Apply the principles and properties of nonlinear relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 50 | D | |
| 51 | C | |
| 52 | A | |
| 53 | A |
out of 4
Subarea 2 (Objectives 0003–0007) Total out of 31
Subarea 3 : Geometry and Measurement
Objective 0008: Apply principles, concepts, and procedures related to measurement.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 54 | C | |
| 55 | A | |
| 56 | D | |
| 57 | B | |
| 58 | D |
out of 5
Objective 0009: Apply the principles of Euclidean geometry and proof.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 59 | A | |
| 60 | C | |
| 61 | D | |
| 62 | A | |
| 63 | B |
out of 5
Objective 0010: Apply properties of two- and three-dimensional figures.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 64 | C | |
| 65 | B | |
| 66 | B | |
| 67 | C |
out of 4
Objective 0011: Apply the principles and properties of coordinate and transformational geometries.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 68 | A | |
| 69 | B | |
| 70 | A | |
| 71 | D | |
| 72 | D | |
| 73 | C | |
| 74 | A |
out of 7
Subarea 3 (Objectives 0008–0011) Total out of 21
Subarea 4 : Statistics and Probability
Objective 0012: Understand the principles, techniques, and applications of statistics.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 75 | C | |
| 76 | A | |
| 77 | C | |
| 78 | A | |
| 79 | C |
out of 5
Objective 0013: Understand the principles of probability.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 80 | C | |
| 81 | B | |
| 82 | A | |
| 83 | C | |
| 84 | B | |
| 85 | B |
out of 6
Subarea 4 (Objectives 0012–0013) Total out of 11
Practice Test Score Calculation
The practice test score calculation is provided so that you may better gauge your performance and degree of readiness to take an MTEL test at an operational administration. Although the results of this practice test may be used as one indicator of potential strengths and weaknesses in your knowledge of the content on the official test, it is not possible to predict precisely how you might score on an official MTEL test.
The Sample Responses and Analyses for the open-response items may help you determine whether your responses are more similar to the strong or weak samples. The Scoring Rubric can also assist in estimating a score for your open responses. You may also wish to ask a mentor or teacher to help evaluate your responses to the open-response questions prior to calculating your total estimated score.
How to Calculate Your Practice Test Score
Review the directions in the sample below and then use the blank practice test score calculation worksheet to calculate your estimated score.
Multiple-Choice Section
| Enter the total number of multiple-choice questions you answered correctly: | 50 | ||
| Use Table 1 below to convert that number to the score and write your score in Box A: | A: | 189 |
Open-Response Section
| Enter the number of points (1 to 4) for your first open-response question: | 3 | ||
| Enter the number of points (1 to 4) for your second open-response question: | 3 | ||
| Add those two numbers (Number of open-response question points): | 6 | ||
| Use Table 2 below to convert that number to the score and write your score in Box B: | B: | 52 |
Total Practice Test Score (Estimated MTEL Score)
| Add the numbers in Boxes A and B for an estimate of your MTEL score: | A + B = | 241 |
Practice Test Score Calculation Worksheet: Middle School Mathematics (65)
Table 1:
| Number of Multiple-Choice Questions Correct | Estimated MTEL Score |
|---|---|
| 0 to 25 | 155 |
| 26 to 30 | 162 |
| 31 to 35 | 169 |
| 36 to 40 | 176 |
| 41 to 45 | 182 |
| 46 to 50 | 189 |
| 51 to 55 | 196 |
| 56 to 60 | 203 |
| 61 to 65 | 210 |
| 66 to 70 | 217 |
| 71 to 75 | 224 |
| 76 to 80 | 230 |
| 81 to 85 | 237 |
| 86 to 90 | 244 |
| 91 to 95 | 251 |
| 96 to 100 | 258 |
Table 2:
| Number of Open-Response Question Points | Estimated MTEL Score |
|---|---|
| 2 | 36 |
| 3 | 40 |
| 4 | 44 |
| 5 | 48 |
| 6 | 52 |
| 7 | 56 |
| 8 | 60 |
Use the form below to calculate your estimated practice test score.
Multiple-Choice Section
| Enter the total number of multiple-choice questions you answered correctly: | |||
| Use Table 1 above to convert that number to the score and write your score in Box A: | A: |
Open-Response Section
| Enter the number of points (1 to 4) for your first open-response question: | |||
| Enter the number of points (1 to 4) for your second open-response question: | |||
| Add those two numbers (Number of open-response question points): | |||
| Use Table 2 above to convert that number to the score and write your score in Box B: | B: |
Total Practice Test Score (Estimated MTEL Score)
| Add the numbers in Boxes A and B for an estimate of your MTEL score: | A + B = |
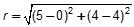 = 5
= 5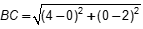 =
= 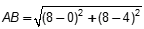 =
=