Practice Test: Mathematics (63)
Answer Key, Sample Responses, Evaluation Chart, and Score Calculation Tool
Answer Key
Fill in your answers below and then print this answer key to save your work. Alternatively, you can print the answer key first to fill it out offline as you take the practice test. Note that the correct responses will be displayed on the printed answer key, so you may want to cover them until you have completed the practice test and are ready to check your answers.
When you have finished the practice test, click on "show answers" to see how well you did on each objective. In addition, use the Evaluation Chart to determine how many questions within each objective you answered correctly.
You will not receive a score for the practice test, and there is no passing score for the practice test. However, to get a sense of how well you did, use the Score Calculation Tool to better gauge your performance and degree of readiness to take an MTEL test at an operational administration.
NOTE: When you take the actual test, you will receive a score report that provides subarea-level performance, not objective-level performance. Information about test results can be found at Score Report Explanation.
| Question Number | Your Response | Correct Response |
Related Objectives and Rationale |
||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | B |
Objective 001 Correct Response: B. Let p = the price the owner paid for a shirt. Then 1.2p is the amount the first shirt is sold for. The cost of 2 shirts during the sale is 1.2 p + 1.2 p divided by 2 = 1.8 p Thus, 1.8 p divided by 2 = 0.9 p is the sale price of one shirt. Since the owner paid p for the shirt, p minus 0.9 p = 0.1 p = 10% of p is the loss on each shirt. Incorrect Response: A.This response could be the result of thinking there is a 20% profit on the first shirt bought on sale and a 10% profit on the second shirt. This is incorrect because both the cost of the second shirt and its 20% markup must be halved to determine its selling price. By this line of reasoning, there is an average profit of 15% for each shirt—a difference of 20% minus 15% = 5%. Incorrect Response: C.This response could be the result of forgetting to divide 1.8p by 2 and thinking that 1.8p is the sale price for 2 shirts, so 2p minus 1.8p = 0.2p = a 20% loss. Incorrect Response: D.This response could be the result of thinking that a customer pays 100% of the retail price for the first shirt, 50% of the retail price for the second shirt, resulting in (100% + 50%) divided by 2 = 75% of the retail price per shirt, so the owner loses 25% per shirt. |
|||||||||||||||||||||||||
| 2 | B |
Objective 001 Correct Response: B. Substitute the values given for p, l, and A: 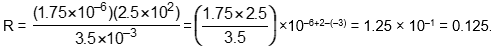
R = 1.75 times 10 to the negative 6 power times 2.5 times 10 to the second power divided by 3.5 times 10 to the negative third power. This equals 1.75 times 2.5 divided by 3.5 times 10 to the power of negative 6 + 2 minus negative 3. This equals 1.25 times 10 to the negative first power. This equals 0.125.
Incorrect Response: A. This response could be the result of attempting to perform the calculation shown in the correct response but then incorrectly subtracting the negative 3 exponent: Negative 6 + 2 minus 3 = negative 7 . Incorrect Response: C. This response could be the result of incorrectly interpreting 0.125 as 1.25 times 10 to the first power . Incorrect Response: D. This response could be the result of multiplying and dividing the exponents, Negative 6 times 2 divided by negative 3 , rather than adding and subtracting them. |
|||||||||||||||||||||||||
| 3 | A |
Objective 001 Correct Response: A. Since all arrangements are identical and they all are used, the number of arrangements is the greatest common factor of the number of flowers. There are 192 roses (16 times 12), 160 lilies, and 128 carnations. 192 = 2 to the 6 power times 3, 160 = 2 to the fifth power times 3, and 128 = 27. The greatest common factor is 2 to the fifth power = 32 arrangements. There are 480 flowers, so there are 480 divided by 32 = 15 flowers in each arrangement. Incorrect Response: B. This response could be the result of forgetting to multiply 16 by 12 (i.e., there are 16 dozen roses), then responding with the number of arrangements rather than the number of flowers in each. The greatest common factor of 16, 160, and 128 is 16. Thus, this error would give 16 flowers per arrangement. Incorrect Response: C. This response could be the result of calculating the number of arrangements as 16 as in response B, then dividing the number of flowers, 480, by 16 to get 30 flowers per arrangement. Incorrect Response: D. This response is the number of arrangements, not the number of flowers in each arrangement. |
|||||||||||||||||||||||||
| 4 | C |
Objective 001 Correct Response: C. The relationships that appear in the computation may be restated with multiplication as D times the number represented by c tens and d ones plus b equals b hundreds a tens and e ones , where each letter represents a digit (i.e., cd represents a 2-digit number and b a e represents a 3-digit number). Divide both sides of the equation by d to obtain the sum cd + b divided by d represents the product of digits c and d plus the fraction b divided by d. This may be expressed as the mixed number The mixed number with whole number digits of c and d and a fraction of b divided by d. Incorrect Response: A. This equation misinterprets the value of b to represent "b tenths" of a unit. This would only be true when the divisor is 10, and this cannot be true for the work shown because divisor d must be a digit from 1 to 9. Incorrect Response: B. This is incorrect because the remainder must also be divided by d. As an example of why this is incorrect, let b a e be the number 126 and d be the number 5. The equation shown then implies that (126 divided by 5) = 25 + 1 = 26. However, 25 times 5 = 125 and 26 times 5 = 130. The correct division is 126 divided by 5 equals the quantity 125 plus 1 divided by 5 equals 25 plus 1 divided by 5 . Incorrect Response: D. This equation shows the remainder, b, being divided by the dividend, b a e . This is incorrect. The remainder must also be divided by the divisor. |
|||||||||||||||||||||||||
| 5 | C |
Objective 001 Correct Response: C. The area of the rectangle is equal to The square root of 3 times open paren the square root of 3 plus square root of 5 close paren . By the distributive property, this becomes The square root of 9 plus the square root of 15 is approximately 3 + 3.9 is approximately 7 . Incorrect Response: A. This response may reflect a misapplication of the distributive property: The square root of 3 times the square root of 3 plus square root of 5 is approximately equal to 3 plus 2 point 2 is approximately 5 . It may also reflect the misconception that The square root of 3 plus the square root of 5= 8 , which leads to the conclusion that The square root of 3 times open parent the square root of 3 + the square root of 5 equals the square root of 3 times the square root of 8 equals the square root of 24 is approximately 5 . Incorrect Response: B. This response may be the result of interpreting a square root to mean "half" (e.g., The square root of 3 equals 3 halves and The square root of 5 equals 5 halves): 3 halves times open paren 3 halves + 5 halves close paren = 3 halves times 4 = 6. Incorrect Response: D. This response may be the result of an estimation error. If The square root of 3 and the square root of 5 are both estimated to be 2 (perhaps by reasoning that an overestimation from approximating The square root of 3 as 2 is counterbalanced by an underestimation from approximating The square root of 5 as 2), then the calculation would be 2 times the quantity 2 + 2 = 8 |
|||||||||||||||||||||||||
| 6 | B |
Objective 002 Correct Response: B. The first four terms are shown below for c = i. 1st term: i 2nd term: I squared plus I equals negative 1 plus i 3rd term: Open paren negative 1 plus I close paren squared plus I equals 1 minus 2i plus I squared plus I equals negative i. 4th term: Open paren negative I close paren squared plus I equals negative 1 plus i The second and fourth terms have a nonzero real part. Incorrect Response: A. This response may be the result of a misconception with complex numbers or an error applying the algorithm shown. Incorrect Response: C. This response may be the result of a misconception with complex numbers or an error applying the algorithm shown. Incorrect Response: D. This response may be the result of a misconception with complex numbers or an error applying the algorithm shown. |
|||||||||||||||||||||||||
| 7 | B |
Objective 002 Correct Response: B. Let the column vector 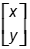 represent a vertex on the square shown. The result of the matrix multiplication represent a vertex on the square shown. The result of the matrix multiplication 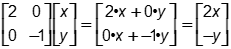 A 2 by 2 matrix with elements 2 0 0 negative 1 is right multiplied by the column vector x y. It equals the column vector with entries 2 x plus 0 y and 0 x plus negative 1 y. This simplifies to the column vector 2x and negative y can be summarized in arrow notation as (x, y)to (2x, negative y). This multiplication moves vertices A (1, 0), B (2, 0), C (2, 1), and D (1, 1) to A prime (2, 0), B prime (4, 0), C prime (4, negative 1), and D prime (2, negative 1). A 2 by 2 matrix with elements 2 0 0 negative 1 is right multiplied by the column vector x y. It equals the column vector with entries 2 x plus 0 y and 0 x plus negative 1 y. This simplifies to the column vector 2x and negative y can be summarized in arrow notation as (x, y)to (2x, negative y). This multiplication moves vertices A (1, 0), B (2, 0), C (2, 1), and D (1, 1) to A prime (2, 0), B prime (4, 0), C prime (4, negative 1), and D prime (2, negative 1).
Incorrect Response: A. This response does not show the value of the x-coordinates being doubled. Instead, the width of the square is doubled while the lower left vertex is left anchored at its original location. Incorrect Response: C. The transformation in this response represents a reflection over the y-axis and a vertical stretch that doubles the value of each y-coordinate. This could be described by the matrix multiplication 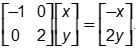 A 2 by 2 matrix with elements negative 1 0 0 2 is right multiplied by the column vector x y. It equals the column vector with entries negative x and 2y A 2 by 2 matrix with elements negative 1 0 0 2 is right multiplied by the column vector x y. It equals the column vector with entries negative x and 2y
Incorrect Response: D. The transformation in this response shows a horizontal shift of 2 units left and a vertical stretch that doubles the value of each y-coordinate. This is not consistent with the transformation matrix provided. |
|||||||||||||||||||||||||
| 8 | B |
Objective 002 Correct Response: B. The vector (3, 4) extends from the point (0, 0) to the point (3, 4) and has a magnitude of 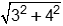 = 5 miles. The boat traveled 50 miles, which is 10 times the magnitude of this vector, in this direction. Therefore, the boat is located at point (30, 40). From here the boat travels directly to point (50, 48). The vector Open paren 50 minus 30 48 minus 40 close paren equals the vector 20 8 describes the direction it will travel. This may be scaled down by a factor of 4 to obtain (5, 2). = 5 miles. The boat traveled 50 miles, which is 10 times the magnitude of this vector, in this direction. Therefore, the boat is located at point (30, 40). From here the boat travels directly to point (50, 48). The vector Open paren 50 minus 30 48 minus 40 close paren equals the vector 20 8 describes the direction it will travel. This may be scaled down by a factor of 4 to obtain (5, 2).
Incorrect Response: A. Consider a proof by contradiction: If this were true, then The vector 30 40 plus the vector a a equals the vector 50 48 for some value of a. No such value exists. Therefore, the boat will not reach the island by traveling along vector (1, 1). Incorrect Response: C. This response may result from the reasoning described for response D along with a transposition of the vector components. Incorrect Response: D. This response may result from reasoning that the boat has reached (6, 8) after 2 hours. The misconception is that the boat would only have traveled 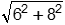 = 10 miles if this were true. The vector 50 minus 6 48 minus 8 equals the vector 44 40 equals the vector 11 10 describes the direction the boat would travel to reach the island. = 10 miles if this were true. The vector 50 minus 6 48 minus 8 equals the vector 44 40 equals the vector 11 10 describes the direction the boat would travel to reach the island.
|
|||||||||||||||||||||||||
| 9 | A |
Objective 002 Correct Response: A. The matrix multiplication AB is performed as follows: 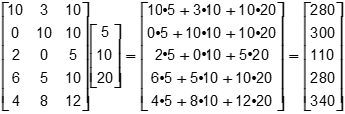
A 5 by 3 matrix contains entries as follows. Row 1 10, 3, 10 Row 2 0, 10, 10 Row 3 2, 0, 5 Row 4 6, 5, 10 Row 5 4, 8, 12. It is right multiplied by the column vector 5, 10, 20. This equals a new 5 by 1 column vector with expressions for entries. The entries represent the inner product between each row of the matrix and the column vector, where Row 1 equals 10 times 5 plus 3 times 10 plus 10 times 20, Row 2 equals 0 times 5 plus 10 times 10 plus 10 times 20, and so on. This simplifies to the column vector 280, 300, 110, 280, 340.
The elements of this column matrix represent the total cost of all meals for each of the five days.
Incorrect Response: B. This response would follow if matrix B were written as a different matrix: 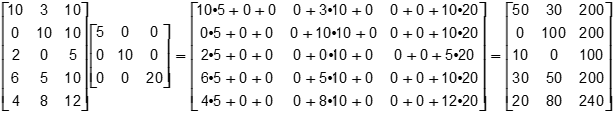
A 5 by 3 matrix contains entries as follows. Row 1 10, 3, 10 Row 2 0, 10, 10 Row 3 2, 0, 5 Row 4 6, 5, 10 Row 5 4, 8, 12. It is right multiplied by a square matrix with diagonal entries of 5, 10, and 20 and non-diagonal entries of 0. This yields a new 5 by 3 matrix with entries that are represented by inner product expressions. The left element of Row 1 represents the inner product of 10 3 10 with 5 0 0. It is written as 10 times 5 plus 0 plus 0. The middle element in Row 1 represents the inner product of 10 3 10 with 0 10 0. It is written as 0 plus 3 times 10 plus 0. The right element in Row 1 represents the inner product of 10 3 10 with 0 0 20. It is written as 0 plus 0 plus 10 times 20. This pattern continues for each row, where the entries in each row of the left matrix form inner products with each of the columns in the right matrix.
The result of these operations yields a 5 by 3 matrix contains entries as follows. Row 1 50, 30, 200 Row 2 0, 100, 200 Row 3 10, 0, 100 Row 4 30, 50, 200 Row 5 20, 80, 240.
Incorrect Response: C. This response would follow if the result from incorrect response B were left multiplied by a row of 1s: 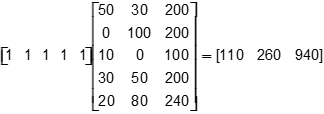
A 5 element row vector is right multiplied by a 5 by 3 matrix contains entries as follows. Row 1 50, 30, 200 Row 2 0, 100, 200 Row 3 10, 0, 100 Row 4 30, 50, 200 Row 5 20, 80, 240. It yields a 3-element row vector with entries 110, 260, 940
To see why this is true, consider the calculation that resulted in 110: 50 times 1 + 0 times 1 + 10 times 1 plus 30 times 1 + 20 times 1 . Incorrect Response: D. This response could be obtained by totaling the elements in the column vector shown in the correct response. This would occur if the column vector in that result were left-multiplied by a row matrix of 1s: A 5-element row vector with uniform entries of 1 is right multiplied by a column vector with entries 280, 300, 110, 280, and 340. It yields a single element matrix with the expression 280 plus 300 plus 110 plus 280 plus 340 as its entry. This equals the 1 by 1 matrix 1310. |
|||||||||||||||||||||||||
| 10 | A |
Objective 002 Correct Response: A. The vectors may be added together by using the head-to-tail method, as shown. The resultant vector is vertical because the horizontal components of t and s are equal and opposite. 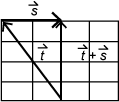
Three vectors are shown in the first quadrant of the coordinate plane. Vector t begins at the point 2, 0 and ends with an arrowhead at the point 0, 4. Vector s begins at the point 0, 4 and ends with an arrowhead at 2, 4. Another vector that is labeled as the sum of vector t plus vector s begins at 2, 0 and ends with an arrowhead at the point 2, 4.
Incorrect Response: B. This vector represents negative (t + s). Incorrect Response: C. This vector represents (t + 2s). Incorrect Response: D. This vector represents negative t. |
|||||||||||||||||||||||||
| 11 | B |
Objective 003 Correct Response: B. One strategy is to multiply by one in the form of X squared divided by x squared , then Rational expression with a numerator of x to the negative first power minus x and a denominator of x to the negative second power minus x squared is multiplied by x squared divided by x squared. This yields the rational expression with numerator x minus x cubed and denominator 1 minus x to the fourth power. Factor the numerator and denominator to get A rational expression with a numerator of x times quantity 1 minus x squared and a denominator written as the product two binomial factors. Those binomials are 1 + x squared and 1 minus x squared. which simplifies to yield X divided by the binomial 1 plus x squared Incorrect Response: A. This response may be the result of clearing fractions in both numerator and denominator by erroneously using different multipliers. Consider the expression written as Given that x is greater than 1, which of the following expressions is equivalent to the quotient of the expression x to the negative first power minus x divided by the expression x to the negative second power minus x squared? If the numerator is multiplied by x and the denominator is multiplied by x squared , the expression becomes A rational expression with numerator 1 minus x squared and denominator 1 minus x to the fourth power. . When the denominator is factored to get the product of the binomial factors 1 + x squared and 1 minus x squared the expression simplifies to 1 over quantity 1 plus x squared . Incorrect Response: C. This response may be the result of erroneously rewriting the given expression as the difference A difference of two rational expressions. The first rational expression has numerator x to the minus 1 and denominator x to the minus 2. The second rational expression is x over x squared. which then simplifies to x minus quantity 1 over x and can be rewritten as The rational expression with numerator X squared minus 1 and denominator X Incorrect Response: D. This response may be the result of erroneously rewriting the given expression as A sum of two rational expressions. The first rational expression has numerator X to the minus 1 and denominator X to the minus 2. The second rational expression is x over x squared. which simplifies to x + quantity 1 over x and can be rewritten as The rational expression with numerator X squared plus 1 and denominator X |
|||||||||||||||||||||||||
| 12 | A |
Objective 003 Correct Response: A. The inequality 6Y plus 9A is greater than or equal to 1,800 represents the student's goal for ticket sales. Solving the inequality for A yields the correct result: The inequality of 9A is greater than or equal to 1,800 minus 6Y is equivalent to the inequality A is greater than or equal to 1,800 divided by 9 minus 6 divided by 9 times Y. This is equivalent to the inequality A is greater than or equal to 200 minus two thirds Y. This is equivalent to A is greater than or equal to negative two thirds Y plus 200. Incorrect Response: B. This response may be the result of transposing the variables (charging $6 for an adult ticket and $9 for a youth ticket) and then solving the equation 9Y plus 6A is greater than or equal to 1,800 for A. Incorrect Response: C. This response may be the result of manipulating the inequality incorrectly. Subtracting 6Y from both sides yields 9A is greater than or equal to negative 6Y plus 1,800 . Response C may be the result of dividing only the value of 1800 by 9 instead of dividing the entire equation by 9. Incorrect Response: D. This response may be the result of transposing the variables in the original equation and then incorrectly solving for A by only dividing 1800 by 6. |
|||||||||||||||||||||||||
| 13 | B |
Objective 003 Correct Response: B. The associative property relates to the grouping of addends or factors. For multiplication: if a, b, and c are real numbers, then A times open paren b times c close paren equals open paren a times b close paren times c. . Incorrect Response: A. The commutative property relates to the order in which numbers are added or multiplied. For multiplication: if a and b are real numbers, then A times b equals b times a . Incorrect Response: C. The distributive property describes how multiplication can be applied to the sum or difference of two (or more) terms: if a, b, and c are real numbers, then A times open paren b plus or minus c close paren equals a b plus or minus a c. . Incorrect Response: D. The transitive property of equality states: if a, b, and c are real numbers and if a = b and b = c, then a = c. |
|||||||||||||||||||||||||
| 14 | A |
Objective 003 Correct Response: A. The technique of completing the square can be used to derive the quadratic formula x equals a rational expression with numerator b squared plus or minus the begin square root b squared minus 4 times a c end root and denominator 2 a To obtain this formula from a times x squared plus b times x plus c equals 0 , subtract c from each side of the equation and then divide each term by . x squared plus b over a times x equals negative c over a The left side of this equation can be factored as the square of the quantity x plus k if it is written as a trinomial of the pattern x squared plus 2 times k times x plus k squared . If B over a = 2k, then k = B over quantity 2 times a and k squared = B squared over 4 a squared. It follows that the equation may be written as x squared plus b over a times x plus b squared over 4 times a squared equals the sum of two terms. The first term is negative c over a and the second term is b squared over 4 times a squared , which is the correct response. For additional context, factor the left side, take the square root, and solve for x: Three equations are shown to be equal to each other. Equation 1 reads open paren x plus fraction with numerator b and denominator 2a close paren squared equals the fraction negative c over a plus the fraction with numerator b squared and denominator 4 times a squared. Equation 2 reads x plus b over quantity 2 times a equals plus or minus the square root of the difference of two terms. The first term is the fraction with numerator b squared and denominator 4 times a squared. The second term is c over a. Equation 3 reads x equals negative b over the product of 2 times a plus or minus the square root of the rational expression with numerator b squared minus 4 a c and denominator 4 times a squared. This is equivalent to the form of the quadratic formula shown above. Incorrect Response: B. This response is the result of squaring B over a instead of B over quantity 2 times a and adding B squared over a squared to both sides of X squared plus b over a times x equals negative c over a . The left side of this equation does not factor in the form the square of the quantity x plus k . Incorrect Response: C. This response is the result of forgetting to divide negative c by a, but squaring B over quantity 2 times a correctly and adding it to both sides of X squared plus b over a times x equals negative c . Incorrect Response: D. This response is the result of making both errors in responses B and C. |
|||||||||||||||||||||||||
| 15 | D |
Objective 003 Correct Response: D. The complex roots of a polynomial occur in conjugate pairs: If 3 + i is a root, then 3 minus i is also a root. The product The binomial x minus quantity 3 plus I times the binomial x minus the quantity 3 minus I equals x squared minus 6 x plus 10 must be a quadratic factor of P of x . Incorrect Response: A. This response is the result of pairing the negative 2 root with a positive 2 root and finding the product The binomial x plus 2 times the binomial x minus 2 . The result might be a factor of P of x , but it does not have to be. Incorrect Response: B. This response is the result of calculating The square of the quantity x plus 2 , which might be a quadratic factor of P of x , but it does not have to be. Incorrect Response: C. This response is the result of identifying the conjugate of 3 + i as 3 minus i, finding the product The binomial x minus quantity 3 plus I times the binomial x minus the quantity minus 3 minus I , and rewriting the negative 6i term as negative 6x . |
|||||||||||||||||||||||||
| 16 | A |
Objective 003 Correct Response: A. The expression X squared plus 6 x minus 55 factors into the product . The binomial factor of x minus 5 times the binomial factor of x plus 11 If x is less than Negative 11 , then The quantities x + 11 and x minus 5 will both be negative numbers, which results in a positive product. If x is greater than 5, then both binomials are positive numbers, so the result is a positive product. This may also be seen graphically: A graph of a parabola plotted with a dashed line is shown. It opens upward, has roots at negative 11 and 5, and the area below its curve is shaded. Incorrect Response: B. This inequality is true only if Negative 11 is less than x is less than 5 since this leads to a negative product of the binomials . The quantities x minus 5 and x plus 11 Incorrect Response: C. The expression X squared minus 6 x minus 55 factors into the product . The quantities x minus 11 and x plus 5 For , X is less than negative 11 both binomials are negative numbers, which produces a positive result. However, when x is greater than 5, there are values for which (x minus 11) is negative and (x + 5) is positive. The inequality X squared minus 6 x minus 55 is greater than 0 does not hold true for those values of x. Incorrect Response: D. The expression X squared minus 6 x minus 55 factors into the product . The quantities x minus 11 and x plus 5 For , X is less than negative 11 both binomials must be negative numbers, which implies a positive product. |
|||||||||||||||||||||||||
| 17 | C |
Objective 004 Correct Response: C. In Stage 1, 1 ninth of the total square is shaded. In Stage 2, each unshaded ninth of the square is divided into 9 again, so each of the new smaller shaded squares represents 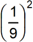 of the original area. Since 8 of those squares are shaded, the sum of the smaller squares in Stage 2 is
8 times the square of one ninth
and the total shaded area is the sum of Stage 1 and Stage 2:
One ninth plus 8 times the square of One ninth.
Each subsequent iteration will introduce 8 times as many shaded squares as the previous iteration, with each new square having
One ninth
the previous size. This results in the expression of the original area. Since 8 of those squares are shaded, the sum of the smaller squares in Stage 2 is
8 times the square of one ninth
and the total shaded area is the sum of Stage 1 and Stage 2:
One ninth plus 8 times the square of One ninth.
Each subsequent iteration will introduce 8 times as many shaded squares as the previous iteration, with each new square having
One ninth
the previous size. This results in the expression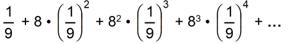
1 ninth plus 8 times 1 ninth squared plus 8 squared times 1 ninth cubed plus 8 cubed times 1 ninth to the fourth plus and so on
Incorrect Response: A. This expression implies that only one smaller square from a divided ninth is added in each stage after Stage 1. Incorrect Response: B. This expression does not describe the pattern because the size of the shaded sections in Stage 1, 1 ninth, does not decrease as the pattern continues. Note that the sum of this expression exceeds 1 by Stage 3. Incorrect Response: D. After Stage 1, the pattern shades 8 smaller squares around each square drawn in the last round, so this number grows exponentially as 8 to the power of quantity n minus 1 . This expression in this response describes the pattern as adding 9 squares for each stage after Stage 1. |
|||||||||||||||||||||||||
| 18 | C |
Objective 004 Correct Response: C. If the pattern continues, then the function repeats itself every 2 units (i.e., the graph is periodic with a period of 2). This means that any multiple of 2 may be added or subtracted from x without changing the value of the function F of x = f of x + 2n where n is an integer. Subtracting 16 (a multiple of 2) from 35 over 2 yields 3 over 2. Therefore, F of 35 halves equals f of 3 halves Incorrect Response: A. This response may be the result of misinterpreting the period of the function to be equal to 3: 35 over 2 minus 3 times 5 equals 2 point 5 equals 5 halves Incorrect Response: B. This response may be the result of misinterpreting the period of the function to be equal to 1.5: 35 over 2 minus 1 point 5 times 11 equals 1 Incorrect Response: D. This response may be the result of mistaking the period of the function to be the equivalence value. |
|||||||||||||||||||||||||
| 19 | C |
Objective 004 Correct Response: C. A function is a relation that assigns each element of set X (called the "domain," which is commonly referred to as "input values" or "x-coordinates") to exactly one element of set Y (called the "range," which is commonly referred to as "output values" or "y-coordinates"). For this graph, each element in the domain Open brace negative 3 negative 2 0 2 3 5 close brace is assigned exactly one value in the range. Incorrect Response: A. The elements negative 3 and 2 in the domain are both assigned to more than one value in the range. Functions do not have more than one y-value assigned to each x-value. Incorrect Response: B. The element 4 in the domain is assigned to more than one value in the range. Functions do not have more than one y-value assigned to each x-value. Incorrect Response: D. Solving the equation for y produces Y equals plus or minus the square root of the quantity x plus 1 so y generally has 2 values assigned to each value of x. For example, when x = 3, y could have the value of 2 or negative 2 . Functions do not have more than one y-value assigned to each x-value. |
|||||||||||||||||||||||||
| 20 | B |
Objective 004 Correct Response: B. The function F of x equals x squared plus 2 x plus 5 is a parabola that opens upward, with a vertex located at X comma f of x where x = Negative b over quantity 2 times a equals negative 2 over quantity 2 times 1 equals negative 1 The parabola has a vertex at The coordinate negative 1 comma f of negative 1 or Open paren negative 1 comma 4 close paren The range of the parabola is Open bracket 4 comma infinity close paren, i.e. F of x is greater than or equal to 4 The composition g of F of x means that this range becomes the set of possible inputs for g of x . The values that g of x may reach given these inputs extends from the square root of 4 to infinity. Therefore, the range of h of x is greater than or equal to 2 Incorrect Response: A. This response represents the domain of g of x , not h of x . Incorrect Response: C. This response could be the result of an error when solving the equation X squared plus 2 x plus 5 is greater than or equal to 0 by completing the square. Incorrect Response: D. This response represents the domain of the function f of x , not the range of h of x . |
|||||||||||||||||||||||||
| 21 | C |
Objective 004 Correct Response: C. Applying the inverse of a function, f superscript minus 1 of x , to the output of the original function, f of x , yields the input for the original function, x. Incorrect Response: A. This response is the result of the misconception that f superscript minus 1 of x equals f of minus x Note that the composition function f superscript minus 1 of f of x equals 2 minus x plus 2 does not return x. Incorrect Response: B. This response is the result of the misconception that the x variables and constants swap positions in an inverse function. Note that the composition function f superscript minus 1 of f of x equals 2 to the power of the square of x does not return x. Incorrect Response: D. This response reflects the misconception that applying the inverse of a function to the original function yields the multiplicative identity element. |
|||||||||||||||||||||||||
| 22 | B |
Objective 005 Correct Response: B. Set the two equations equal to each other to determine the values for m that do have points of intersection: The equation m x plus 3 equals minus x squared plus 3 x plus 2 is equivalent to x squared plus open paren m minus 3 close paren times x plus 1 equals 0. Substitute the coefficients into the quadratic formula to obtain X equals a rational expression with a numerator of the negative of the binomial m minus 3 plus or minus begin square root of the square of the binomial m minus 3 minus 4 times 1 times 1 end root and denominator 2 times 1. Real values of x correspond to points of intersection; therefore, determine where the radicand is negative: The inequality open paren m minus 3 close paren squared minus 4 is less than 0 is equivalent to the inequality m squared minus 6 m plus 5 is less than 0 is equivalent to the binomial m minus 1 times the binomial m minus 5 is less than 0 The product on the left side will only be negative when one factor is positive and the other negative. This occurs in the interval . 1 is less than m is less than 5 Incorrect Response: A. This inequality could be the result of solving open paren m plus 3 close paren squared minus 4 is less than 0 . Incorrect Response: C. This inequality could be the result of solving open paren m plus 3 close paren squared minus 4 is greater than 0 . Incorrect Response: D. This inequality represents the values for m for which the two graphs will intersect. |
|||||||||||||||||||||||||
| 23 | B |
Objective 005 Correct Response: B. The absolute value function y equals the begin absolute value x plus b end absolute value plus c is symmetrical about the coordinate minus b comma c the point of its vertex. It is a piece-wise function made of two linear functions: the linear function extending toward positive x has a slope of 1, and the linear function extending toward negative x has a slope of negative 1. Use the latter slope to move from the point the coordinate minus 6 comma 13 to the coordinate minus 6 minus 2 comma 13 plus 2 equals the coordinate minus 8 comma 15 as shown in the following graph. The graph of an absolute value function is shown in the upper half of the coordinate plane. It opens upward and has a vertex at 4 comma 3. The coordinates minus 6 comma 13, minus 8 comma 15, and 16 comma 15 are labeled along the plot of this function. This point has the same y-coordinate as (16, 15), so the line of symmetry for this graph is located at the average of these x-coordinates: A fraction with numerator 16 plus negative 8 and denominator of 2 equals 4 Therefore, the vertex is at x = 4. Its y-coordinate may be determined either by moving 10 units to the right from The coordinate negative 6 comma 13 along a slope of negative one, the coordinate negative 6 + 10 comma 13 minus 10 or by moving 12 units to the left from (16, 15) along a slope of negative one, The coordinate 16 minus 12 comma 15 minus 12 Both paths lead to (4, 3). Alternatively, for a more direct solution, describe each side of the absolute value equation by writing linear equations in point-slope form and find their point of intersection by solving the system. The equations Y minus 15 equals 1 times the quantity of x minus 16 and Y minus 13 equals negative 1 times the quantity of x minus negative 6 have a common solution at (4, 3). Incorrect Response: A. This point represents the y-intercept for the function. Incorrect Response: C. This response may be the result of finding the midpoint between the two points. Incorrect Response: D. This response may be the result of multiple errors that build upon each other, such visualizing the absolute value function as opening downward along with arithmetic errors related to the slope. Notice that a line segment that connects points (negative 6, 13) and (8, 23) does not have a slope equal to 1 (or negative 1). |
|||||||||||||||||||||||||
| 24 | B |
Objective 005 Correct Response: B. A parabola written in the standard form of F of x equals a times x squared plus b times x plus c has a vertex located at X equals minus b over 2 a The vertex for f of x is located at X equals minus negative 24 over 4 equals 6 The positive leading coefficient of the function gives the graph upward concavity—this means that its vertex is located at the minimum value of the function and the function always increases in value for values of x that move away from it in either direction. For this reason, x = negative 3 , being the value furthest away from the vertex in the interval Minus 3 is less than or equal to x is less than or equal to 5 generates the highest value for f of x: F of negative 3 equals 2 times the square of negative 3 minus 24 times negative 3 plus 6 equals 96 Incorrect Response: A. This response may be the result of misinterpreting the given interval in the problem: 176 equals f of negative 5 Incorrect Response: C. This response may be the result of the misconception that the function has a maximum value on the interval when x = 5. This may be the result of interpreting the parabola as opening downward instead of opening upward. Incorrect Response: D. The vertex is located at x equals 6, F of 6 equals negative 66 Note that this value is outside the interval of values to be considered. |
|||||||||||||||||||||||||
| 25 | C |
Objective 005 Correct Response: C. The inequality 2 x plus y is greater than or equal to 0 can be expressed as Y is greater than or equal to negative 2 times x In a graph, the boundary of this inequality appears as a solid line passing through the origin with a slope of negative 2. The boundary of the other inequality, X minus y is less than 1 is graphed with a dashed line and with intercepts at x = 1 and y = negative 1. This inequality can also be expressed as Y is greater than x minus 1 Together, these two inequalities admit solutions in the coordinate plane that are above or along the solid line and above the dashed line. The shaded region represents all values that create true statements with both inequalities. Incorrect Response: A. This represents the system of inequalities 2 x plus y is greater than or equal to 0 and x minus y is greater than 1 Incorrect Response: B. This represents the system of inequalities 2 x plus y is less than or equal to 0 and x minus y is greater than 1 Incorrect Response: D. This represents the system of inequalities 2 x plus y is less than or equal to 0 and x minus y is less than 1 |
|||||||||||||||||||||||||
| 26 | A |
Objective 005 Correct Response: A. Given the scenario, only positive values for p and b make sense, so all graphs will be limited to quadrant 1. Constraints on the bakery's production capabilities limit the number of bagels and pretzels it can make each day. These constraints may be expressed as a system of linear inequalities. The inequality 3 b plus p is less than or equal to 12 describes the constraint that the time to bake the bagels and pretzels cannot exceed 12 hours per day. Similarly, 2 b plus 4 p is less than or equal to 16 describes the constraint that the time to prepare the bagels and pretzels cannot exceed 16 hours per day. The correct lines and shading for these combined inequalities form the feasibility region shown in response A. The dashed lines represent the objective function to be maximized (i.e., profit, in this context). Combinations of bagels and pretzels that lie on the same dashed line yield equivalent profits for the bakery, and the further a dashed line is from the origin, the greater its profit. (These lines represent the equation 60b + 50p = k for different values of k, where k represents a given profit—lines further from the origin show greater values for k). The maximum achievable profit occurs at the vertex where the lines bounding the feasible region intersects the second dashed line. Incorrect Response: B. The feasible region in this response represents the system of inequalities 3 b plus p is less than or equal to 12 or 2 b plus 4 p is less than or equal to 16 The feasible region in the correct response represents the system of inequalities 3 b plus p is less than or equal to 12 and 2 b plus 4 p is less than or equal to 16 The bakery cannot produce the combinations of pretzels and bagels beyond the feasible region shown in the correct response. Incorrect Response: C. This response assigns the coefficients for the bagel variables to the pretzel variables and vice versa: 3 b plus p is less than or equal to 12 and 4 b plus 2 p is less than or equal to 16 Incorrect Response: D. This response combines the errors described in responses B and C. |
|||||||||||||||||||||||||
| 27 | A |
Objective 006 Correct Response: A. If the piece of equipment decreases in value by 6% each year, then the equipment retains 100% minus 6% = 94% of its value each year. 42,000 times 0 point 94 can be used to find the equipment's value at the end of the first year. For each subsequent year, the value is 94% of the value from the previous year. This constant ratio indicates that the value of the equipment decays exponentially. The value of the equipment can be determined using the expression 42,000 times 0 point 94 exponent n . Incorrect Response: B. This equation is incorrect because it assumes a constant (rather than exponential) rate of change in the value of the equipment over time. Additionally, using this formula generates a value greater than the initial value for year 2, as 42,000 times 0 point 94 times 2 equals 42,000 times 1 point 88 equals 78,960 Incorrect Response: C. This response is based on a misinterpretation of the correct equation V sub n equals 42,000 times open paren 1 minus 0 point 06 close paren exponent n Incorrect Response: D. This equation shows a linear decrease of 2,520 dollars (6% of the original value) each year instead of the exponential decay of 6% of the value each year. |
|||||||||||||||||||||||||
| 28 | B |
Objective 006 Correct Response: B. The general equation of an exponential function with the x-axis as its horizontal asymptote is Y = a times b exponent x where b is a real number not equal to 1. Substituting (0, 3) into the equation gives 3 equals a times b exponent 0 , b exponent 0 equals 1 so a = 3. Substituting The coordinate negative 2 comma 27 over 4 generates the equation 27 over 4 equals 3 b exponent minus 2 which is equivalent to . 9 over 4 equals 1 over b squared It follows that b = 2 thirds. Incorrect Response: A. This response could be the result of noticing that the y-intercept is given and incorrectly writing the exponential function Y equals b exponent x plus 3 Solving 27 over 4 equals b exponent minus 2 plus 3 results in b = 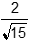 . .
Incorrect Response: C. This response could be the result of thinking as in Response A above, but ignoring or making an error regarding the negative exponent. If 27 over 4 equals b squared plus 3 then b =  . .
Incorrect Response: D. This response could be the result of using Y = a times b exponent x correctly identifying a = 3, then ignoring or making an error regarding the negative exponent. If 27 over 4 equals 3 b squared then b = 3 halves. |
|||||||||||||||||||||||||
| 29 | A |
Objective 006 Correct Response: A. One way to determine the correct response is to take the graph of , Y equals 2 exponent x reflect it over the y-axis to obtain , Y equals 2 exponent minus x and then shift that graph one unit to the left to get the graph of . F of x equals 2 to the power of the quantity 1 minus x The inverse will be represented by the graph resulting from reflecting the graph of F of x equals 2 to the power of the quantity 1 minus x over the line y = x. This is graph A. Alternatively, make a table of values for . F of x equals 2 to the power of the quantity 1 minus x
Incorrect Response: B. This graph is the reflection of the graph of F of x equals 2 to the power of the quantity 1 minus x over the y-axis. Incorrect Response: C. This graph is the reflection of the graph of F of x equals 2 to the power of the quantity 1 minus x over the line y = negative x. Incorrect Response: D. This graph is the reflection of the graph of F of x equals 2 to the power of the quantity 1 minus x over the x-axis. |
|||||||||||||||||||||||||
| 30 | A |
Objective 006 Correct Response: A. The domain of F of x equals log base 4 of quantity x plus 2 is the set of real numbers for which x + 2 greater than 0. Thus x greater than negative 2. Testing values of x close to negative 2 indicates that x = negative 2 is a vertical asymptote. For x = 0, log base 4 of 2 equals one half because  . Then
The coordinate 0 comma one half
is the y-intercept. For y = 0,
log base 4 of quantity x plus 2 equals 0
is equivalent to
x + 2 = 4 to the 0 power; 4 to the zero power = 1
so x = negative 1.
Thus, the x-intercept is The coordinate minus 1 zero . Then
The coordinate 0 comma one half
is the y-intercept. For y = 0,
log base 4 of quantity x plus 2 equals 0
is equivalent to
x + 2 = 4 to the 0 power; 4 to the zero power = 1
so x = negative 1.
Thus, the x-intercept is The coordinate minus 1 zero
Incorrect Response: B. This response may be a result of thinking that when x = 0, log base 4 of 2 equals negative 2 possibly thinking that 4 to the power of negative 2 = 2 . Incorrect Response: C. This response may be a result of thinking that when x equals negative 2 log base 4 of 0 equals 0 and since The coordinate negative 2 comma 0 is an intercept, then x = negative 2 cannot be a vertical asymptote, so the asymptote must then be x = 2 . Incorrect Response: D. This response may be a result of combining the errors made in each of the previous responses. |
|||||||||||||||||||||||||
| 31 | C |
Objective 006 Correct Response: C. If Rational expression with numerator Log base 2 of the quantity x minus 1 and denominator 5 equals 1 then Log base 2 of the quantity x minus 1 equals 5 An equation of the form Log base b of N equals p where b is the base and p is the exponent, may be equivalently written as the equation B to the power of p equals N . This statement says the exponent used on base 2 is 5, so 2 to the fifth power equals x minus 1 . Incorrect Response: A. This response confuses the base with the exponent. Incorrect Response: B. This response has the correct base, but confuses the result with the exponent. Incorrect Response: D. This response confuses the relationship of all three of the values. |
|||||||||||||||||||||||||
| 32 | B |
Objective 006 Correct Response: B. Substitute: F of g of x equals 3 times 2 with the exponential expression log base 2 of quantity one third x. This equals 3 times one third x, which equals x. Incorrect Response: A. This response may reflect algebraic errors with a misconception that these operations cancel each other in a way that 1 is the result, such as with the erroneous claim that Log base 2 of 2 to the power of x equals 1 . Incorrect Response: C. This response may be the result of performing several errors, such as 3 times 2 with the exponential expression log base 2 of quantity one third x is claimed to equal 3 times two to the power of one third x, which is claimed to equal 6 to the power of one third x Incorrect Response: D. This response may be the result of misunderstanding the relationship between exponents and logarithms: 3 times 2 with the exponential expression log base 2 of quantity one third x is claimed to equal 3 times 2 to the power of the quantity one third x. |
|||||||||||||||||||||||||
| 33 | B |
Objective 007 Correct Response: B. A rational function is a function of the form R of x equals p of x over q of x where p and q are polynomial functions, and q is not the zero polynomial. Graphs of rational functions may have vertical and horizontal asymptotes, and the graph in this response has one of each. Incorrect Response: A. This graph does not exhibit behavior consistent with a function that has a polynomial denominator. Incorrect Response: C. This piecewise-defined function holds a constant value in each stretch of its interval. This is not consistent with having a polynomial denominator. Incorrect Response: D. This is a graph of an absolute value function. |
|||||||||||||||||||||||||
| 34 | D |
Objective 007 Correct Response: D. The polynomial has roots at x = negative 4, negative 1, and 2. This indicates that it may be written as P of x equals k times the open paren x plus 4 close paren exponent b times open paren x plus 1 close paren exponent c times open paren x minus 2 close paren exponent d The end behavior of any polynomial of degree n (which here is equal to b + c + d) should resemble the power function F of x equals a times x to the power of n . Because the function is shown increasing without bound when x approaches negative infinity and decreasing without bound as x approaches positive infinity, we can infer that the leading coefficient must be negative and that n is an odd power. Incorrect Response: A. P of x equals negative 0 point 0 3 times the open paren x minus 4 close paren times open paren x minus 1 close paren times open paren x plus 2 close paren This polynomial has roots at x = 4, 1, and negative 2, which is not consistent with the information shown. Incorrect Response: B. P of x equals negative 0 point 0 3 times open paren x plus 4 close paren times open paren x plus 1 close paren times open paren x minus 2 close paren This polynomial has roots located at the correct positions, but the multiplicity of the roots at x = negative 4 and 2 are incorrect. The graph touches, but does not cross, the x-axis at these locations and this indicates these roots must have an even multiplicity (i.e., be raised to an even power). Each of the roots for this polynomial are of the first power, so the graph would cross the axis at these points. Incorrect Response: C. P of x equals negative 0 point 0 3 times open paren x minus 4 close paren squared times open paren x minus 1 close paren times open paren x plus 2 close paren squared This polynomial has roots at x = 4, 1, and negative 2. This is not consistent with the information shown. |
|||||||||||||||||||||||||
| 35 | D |
Objective 007 Correct Response: D. This expression factors into Rational expression with a numerator of quantity x plus 1 times quantity x minus 1 and a denominator of 2 times quantity x plus 1 times quantity x minus 2 The numerator and denominator both contain the factor The quantity (x + 1) and so the graph has a removable discontinuity at x = negative 1. The expression simplifies to One half times quantity x minus 1 divided by quantity x minus 2 with the exclusion x not equal to 1. Since The quantity x minus 2 is a factor of the denominator, the graph has a vertical asymptote at x = 2. Also, because quantity x minus 1 divided by quantity x minus 2 can never equal 1, the value of the function cannot be equal to 1 half, which creates a horizontal asymptote in the graph along y = 1 half. Incorrect Response: A. This graph has a defined value at x = negative 1 (i.e., 0). Its vertical asymptotes occur when the denominator equals zero (which does not include x = 2) and the horizontal asymptote is at y = 0. The horizontal asymptote may be determined by factoring the leading power of x from the numerator and denominator of the rational function: Rational expression with a numerator of x times the binomial 1 plus 1 over x and a denominator of x squared times open paren 1 minus 4 over x minus 4 over x squared close paren behaves as 1 over x for large values of x, and 1 over x approaches 0 as x increases. Incorrect Response: B. This equation simplifies to . Y equals a rational expression with a numerator of x plus 1 and a denominator of 2 times the binomial x plus 1 times the binomial x plus 2 equals a rational expression with a numerator of 1 and a denominator of 2 times the binomial x plus 2. It has a point discontinuity at x = negative 1, a vertical asymptote at x = negative 2, and a horizontal asymptote at y = 0. Incorrect Response: C. This equation has a defined value at x = negative 1 (i.e., 0) and a vertical asymptote at x = negative 2. For very large positive or negative values of x, the equation is approximately equal to 1, which appears in its graph as a horizontal asymptote. |
|||||||||||||||||||||||||
| 36 | C |
Objective 007 Correct Response: C. The two vertices of the rectangle above the x-axis must be directly above those on the x-axis and share the same y-coordinate. The information given describes the first-quadrant vertex at (x, y), where it intersects the function y = 36 minus x squared . Because this function is symmetric above the y-axis, the other upper-vertex coordinate must be located at The coordinate minus x comma y. The area of the rectangle is the product of its width, 2x, and its height, y = 36 minus x squared . This leads to the equation 2 x times open paren 36 minus x squared close paren equals 160 which simplifies as X cubed minus 36 x plus 80 equals 0 Incorrect Response: A. This equation can be obtained from 2 times 6 times open paren 36 minus x squared close paren equals 160 In this response, the roots of the parabola are treated as if they represent the width of the rectangle, and the height is obtained from an unknown—and unrelated—value of x. Incorrect Response: B. This equation can be obtained from 2 times 6 times open paren 36 minus x squared close paren equals 80 In this response, the roots of the parabola area treated as if they represent the width of the rectangle, and the height is obtained from an unknown—and unrelated—value of x. Incorrect Response: D. Describing the width of the rectangle as x rather than 2x leads to the equation x times open paren 36 minus x squared close paren equals 160 |
|||||||||||||||||||||||||
| 37 | B |
Objective 007 Correct Response: B. Factor the polynomials in the equation to obtain A rational expression with a numerator of the binomial x minus 5 times the binomial x plus 3 and a denominator of the binomial x minus 3 times the binomial x plus 3 equals 0. The factors of x + 3 cancel, and the equation A rational expression with a numerator of x minus 5 and a denominator of x minus 3 equals 0 has the solution x = 5. Incorrect Response: A. These values for x represent exclusions from the domain of the function (because the rational expression is undefined there). A graph of the function F of x equals a rational expression with a numerator of x squared minus 2 x minus 15 and a denominator of x squared minus 9 has a removable point discontinuity at x = negative 3 (where the factors of x + 3 cancel) and a vertical asymptote at x = 3. Incorrect Response: C. These values for x represent the solution to the equation, x = 5, and one of the values for which the rational expression is undefined. Incorrect Response: D. These values for x represent the solution to the equation, x = 5, and both values for which the rational expression is undefined. |
|||||||||||||||||||||||||
| 38 | C |
Objective 007 Correct Response: C. The second differences of a sequence defined by a quadratic function are constant and nonzero. The sequence of values produced by F sub 3 of x has first differences of 3, 5, 7, 9 and so on and this sequence has constant second differences of 2. Incorrect Response: A. The sequence of second differences for F sub 1 of x are 3, 5, 7 and so on , which is not constant. The third differences, however, are constant and this could indicate that F sub 1 of x is a cubic polynomial. Incorrect Response: B. The sequence of first differences for F sub 2 of x are constant and its second differences are 0. This indicates that F sub 2 of x could be a linear function. Incorrect Response: D. The sequence of second differences for F sub 4 of x are 1, 2, 3 and so on , which is not constant. The third differences, however, are constant and this indicates that F sub 4 of x may be a cubic polynomial. |
|||||||||||||||||||||||||
| 39 | A |
Objective 008 Correct Response: A. The angle 8 pi over 3 is coterminal with 2 pi over by 3 because 8 pi over 3 minus 2 pi equals 8 pi over 3 minus 6 pi over 3 equals 2 pi over 3 (i.e., the angles originate from the same position—the positive x-axis—and end at the same location on the unit circle). Use the relationships The secant of x equals 1 over the cosine of x and The cosine of quantity pi minus x equals the negative cosine of x to evaluate the expression as follows: 1 over the cosine of two thirds pi equals 1 over the negative cosine of quantity pi minus two thirds pi. This equals negative 1 over the cosine of pi over 3, which equals negative 1 over one half, which equals negative 2. Incorrect Response: B. This response could be the result of computing The negative cosine of pi over 3 rather than  . .
Incorrect Response: C. This response could be the result of computing The sine of 8 pi over 3. Incorrect Response: D. This response could be the result of computing The cosecant of 8 pi over 3. |
|||||||||||||||||||||||||
| 40 | A |
Objective 008 Correct Response: A. The minimum point of Y equals the sine of x over the interval 0 is less than or equal to x is less than or equal to 2 pi occurs at X equals 3 pi over 2 where The sine of 3 pi over 2 equals negative 1 For the minimum point to be located at The coordinate 11 pi over 6 comma negative one half without a vertical shift or change in period, the function must horizontally shift (via a phase shift) to the right by 11 pi over 6 minus 3 pi over 2 equals 2 pi over 6 equals pi over 3 An amplitude of 1 half reduces the minimum value to negative 1 half. Incorrect Response: B. This response uses the correct amplitude, but the phase difference may be based on the minimum value of the sine of x occurring at x = pi . Incorrect Response: C. This response uses the correct phase shift, but the phase difference may be based on an incorrect amplitude for the sine of x . Incorrect Response: D. This response may combine the errors in responses B and C. |
|||||||||||||||||||||||||
| 41 | B |
Objective 008 Correct Response: B. The given information states that the average daily temperature for a city over the span of one year can be modeled by a cosine function with an average daily temperature of T. The additional parameters for the cosine function can be determined from the given information. A cosine function with a minimum value of 16 degrees and a maximum value of 80 degrees has an average value of The sum of 16 degrees plus 80 degrees divided by 2 is 48 degrees and an amplitude of 80 degrees minus 48 degrees equals 32 degrees. The natural period of a cosine function is 2 pi . Multiplying t by 2 pi compresses the period to 1 (i.e., it would have a period of 1 day in this context) and dividing 2 pi t by 365 stretches the period to 365 days. The cosine function must be shifted to the right by 212 days to make its maximum value occur on July 31, which is done by replacing t with t minus 212 . These combined details are captured in the function 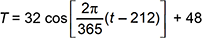 . .
Incorrect Response: A. This response uses a cosine function with an average value of 32 degrees and an amplitude of 48 degrees, which is inconsistent with the information given. Incorrect Response: C. This response uses the reciprocal of the correct period and transposes the average daily temperature value with the amplitude, as described in response A. Incorrect Response: D. This response uses the reciprocal of the correct period. |
|||||||||||||||||||||||||
| 42 | C |
Objective 008 Correct Response: C. rational expression with a numerator of the tangent squared of x and a denominator of 1 plus the tangent squared of x equals the tangent squared of x over the secant squared of x. This is equivalent to rational expression with a numerator of sine squared of x over cosine squared of x and a denominator of 1 over cosine squared of x. This simplifies to sine squared of x. Incorrect Response: A. This may be the result of confusing tangent x with cotangent x and evaluated rational expression with a numerator of the cotangent squared of x and a denominator of 1 plus the cotangent squared of x. Incorrect Response: B. This may be the result of substituting the denominator of the expression with 1 plus the square of the tangent of x equals the secant squared of x and the numerator with the square of the tangent of x equals the secant squared of x minus 1 to obtain rational expression with a numerator of the square of the secant of x minus 1 over a denominator of the square of the secant of x However, this expression does not simplify to the square of the secant of x Incorrect Response: D. This may be the result of substituting the denominator of the expression with 1 plus the square of the cotangent of x equals the cosecant squared of x and the numerator with the square of the cotangent of x equals the cosecant squared of x minus 1 to obtain rational expression with a numerator of the square of the cosecant of x minus 1 over a denominator of the square of the cosecant of x However, this expression does not simplify to the square of the cosecant of x |
|||||||||||||||||||||||||
| 43 | B |
Objective 008 Correct Response: B. This response follows from the transformation multiplying the sine of x by the identity property and expressing the the cotangent of x in terms of other functions: the sine of x times a fraction with a numerator of the sine of x and a denominator of the sine of x is added to the cosine of x times a fraction with the numerator of the cosine of x and denominator of the sine of x. This equals the cosecant of x Incorrect Response: A. This response is the result of multiplying the sine of x to only the left side of the equation. Incorrect Response: C. This response may represent the division of each term by the cosine of x with an error on the right side of the equation: the cosecant of x divided by the cosine of x equals the cosecant of x times the secant of x is not equal to 1 over the sine of x. Incorrect Response: D. This response simplifies the cosine of x times the cotangent of x in an incorrect manner. |
|||||||||||||||||||||||||
| 44 | C |
Objective 009 Correct Response: C. Triangles BDA and DCA as labeled in the diagram shown below have two pairs of congruent angles: Angle D A B is congruent to angle D A C and Angle D B A is congruent to angle A D C . Therefore, the angles are similar by Angle angle similarity , and this justifies the proportion A C over D C equals A D over B D Using the lengths provided, Ratio with a numerator of a plus b and a denominator of e equals the ratio c over d The equation ce = ad + bd represents an equivalent equation. The triangle in the item stem is shown with its vertices labeled with the capital letters D C and A. Vertex D is shown by a 100-degree angle. A line segment, labeled with a lowercase d, is drawn from the 100-degree angle to the opposite side at point labeled capital B, which is located along the segment that contains vertices capital A and capital C. This point divides that into smaller segments, with the segment to the left labeled lowercase a and the segment to its right labeled lowercase b. The line segment from vertex D to point B forms a linear pair of angles with the angle defined by vertices A B and D measuring 100 degrees. This partitions triangle A D C into two smaller triangles. Triangle A D B is located to the left of the segment and triangle B D C is located to the right of the segment. The length of the line segment from vertex A to vertex D is labeled lowercase c and the length of the line segment from vertex D to vertex C is labeled lowercase e. Incorrect Response: A. This equation may be obtained from an incorrect observation that c over a equals e over b Incorrect Response: B. This simplifies to a = b and could be obtained from a misconception that d bisects the bottom edge. Incorrect Response: D. This equation is likely the result of incorrectly claiming pairs of edges represent corresponding parts of similar triangles. |
|||||||||||||||||||||||||
| 45 | C |
Objective 009 Correct Response: C. The volume of the original container can be found using the equation: V sub 1 equals L times w times d The volume of the new container can be found using the equation V sub 2 equals 4 L times 2 w times one half d Regroup the factors and compare with V sub 1: 4 times 2 times one half times L times w times d equals 4 V sub 1 The volume of the new container is 4 times the volume of the original container. Incorrect Response: A. This result could be due to a misconception where the effect of quadrupling the length is counteracted by doubling the width, so halving the depth produces a volume that is half of the original volume. Incorrect Response: B. This result could be due to a misconception where the net effect of quadrupling the length, doubling the width, and halving the depth leaves the volume unchanged. Incorrect Response: D. This result could be due to a computational error where the length is quadrupled, the width is also quadrupled, and the depth is halved. |
|||||||||||||||||||||||||
| 46 | B |
Objective 009 Correct Response B: The volume of the solids can be computed as shown. (Note that for the prism, properties of 30 60 90 triangles must be used to find the height of the triangle.) Square pyramid: V equals one third times x squared times h Cone: V equals Pi over 3 times x squared times h Cylinder: V equals Pi times r squared times h equals pi times open paren x over 2 close paren squared times h equals pi over 4 times x squared times h Prism: V equals B h equals x over 2 times a fraction with a numerator of x times the square root of 3 and a denominator of 2 equals the square root of 3 divided by 4 times x squared times h Since the factor X squared times h is present in all cases, the volumes can be compared using the leading coefficients. The coefficient pi over 3 is the only coefficient greater than one, so the cone has the greatest volume. Incorrect Response: A. This response could be the result of misinterpreting the question as asking for the solid with the least volume. Incorrect Response: C. This response could stem from a misconception that the radius of the cylinder is x, rather than x over 2. Incorrect Response: D. This response may be the result of misinterpreting the value of The square root of 3, or another misconception related to properties of 30 60 90 triangles. |
|||||||||||||||||||||||||
| 47 | D |
Objective 009 Correct Response: D. Using a base radius of 5 cm and a height of 15 cm, the volume of the can is 25 pi times 15 is approximately 1,178 point 09 cubic centimeters The maximum possible error occurs from an underestimate of the volume for the can. Assuming the can has a base radius of 5.49999 cm and a height of 15.49999 cm: 5 point 4 9 9 9 9 squared times pi times 15 point 4 9 9 9 9 is approximately 1,473 point 01 The difference between these values is the maximum possible error in the calculated volume: 1473.01 minus 1178.09 = 294.92 is approximately 294.9 cubic centimeters . Incorrect Response: A. This response represents the difference between the volume of a can with radius of 5.4 and a height of 15.4, , 5 point 4 squared times pi times 15 point 4 is approximately equal to 1,410 point 7 7 cubic centimeters and the estimated volume of that can found by approximating its radius as 5 and its height as 15, . 5 squared times pi times 15 is approximately equal to 1,178 point 0 9 cubic centimeters However, because the values of 5.4 and 15.4 can increase further and still round to 5 and 15, respectively, 232.7 cubic centimeters cannot be the maximum possible error. Incorrect Response: B. This response is the result of the misconception that an overestimate for the volume of the can will produce the maximum possible error. Using a base radius of 4.5 cm and a height of 14.5 cm for the can: . 4 point 5 squared times pi times 14 point 5 is approximately 922 point 4 5 cubic centimeters The difference between the given computation and this value results in an answer of 255.6 cubic centimeters . Incorrect Response: C. The response represents the average of the maximum value for the error calculated in response D with the underestimated value for the error calculated in response B. |
|||||||||||||||||||||||||
| 48 | C |
Objective 010 Correct Response: C. There are two cases for which one pair of rays are collinear. They are either parallel to each other or antiparallel (i.e., they line along the same line but point in opposite directions). Consider these two cases and then draw in the remaining pair of parallel rays, as shown in the following diagram. Two pairs of angles are shown. The top pair of angles have their bottom rays oriented antiparallel to each other. The other rays parallel each other and would overlap if the vertex of the angles overlapped. The bottom pair of angles shows their bottom rays oriented in the same direction. If these rays were moved so that they all shared a common vertex, then there would appear to only be 1 angle because all the corresponding parts would overlap perfectly In the top diagram, the angles are supplementary because they combine to form a straight angle. In the bottom diagram, the angles can be shown to be congruent by reasoning that the collinear rays lie along a transversal that cuts through parallel lines containing the parallel rays. Incorrect Responses A, B, and D. Based on the information shown above, it is clear that these statements are not true. |
|||||||||||||||||||||||||
| 49 | B |
Objective 010 Correct Response: B. The format of an indirect proof requires the assumption that the negation of the conclusion is correct. Thus, assume that Line segment P N bisects Angle Q P R . Use this assumption and other given information to write a list of logical statements until a contradiction of either one of the given pieces of information or a theorem or definition is found. In this case, the assumption and the properties of the isosceles triangle can be used to prove that N must be the midpoint of Line segment Q R , which contradicts the given information about point N. Incorrect Response: A. This response does not match the format of an indirect proof since the assumption is not the negation of the conclusion. Incorrect Response: C. This response does not match the format of an indirect proof since the assumption is not the negation of the conclusion. Incorrect Response: D. This response assumes the negation of the conclusion, but it is not true that Line segment Q R cannot be the base, so a contradiction will not be reached. |
|||||||||||||||||||||||||
| 50 | A |
Objective 010 Correct Response: A. Let x be the measure of the exterior angle. Then 6x + 12 is the measure of the interior angle and x + 6x + 12 = 180. This equation yields x = 24, so the exterior angle measures 24 degrees. The polygon is regular, so the exterior angles are congruent. The sum of the exterior angles of any polygon is 360 degrees. Dividing this by 24 degrees per angle yields 15 angles. It follows that there are 15 sides. Alternatively, one interior angle measures 6 times 24 + 12 = 156 and the formula for the measure of one interior angle of a regular polygon is m equals a rational expression with a numerator of open paren n minus 2 close paren times 180 over a denominator of n where n equals the number of sides. Solving 156 equals a rational expression with a numerator of open paren n minus 2 close paren times 180 over a denominator of n also yields n = 15. Incorrect Response: B. If the number of sides is 18, then each exterior angle measures 360 over 18 equals 20 degrees and each interior angle measures 160 degrees. 160 is not equal to 6 times 20 plus 12 Incorrect Response: C. If the number of sides is 20, then each exterior angle measures 360 over 20 equals 18 degrees and each interior angle measures 162 degrees. 162 is not equal to 6 times 18 plus 12 Incorrect Response: D. Solving the equation x + 6x + 12 = 180 leads to this response. However, 24 represents the measure of one of the exterior angles of the regular polygon described and not its number of sides. |
|||||||||||||||||||||||||
| 51 | A |
Objective 010 Correct Response: A. Since opposite sides of a parallelogram are congruent, they represent congruent chords of the circle and intercept congruent arcs of the circle. Each of the two distinct sets of adjacent sides intercept arcs whose sum is half the circle. The angle of the parallelogram formed by two adjacent sides is therefore inscribed in a semicircle. The measure of an inscribed angle is half the measure of its intercepted arc. Thus, the angle formed by two adjacent sides of the parallelogram is a right angle, and the inscribed parallelogram is a rectangle. Incorrect Response: B. It is possible to inscribe a square in a circle, but the information given is insufficient to guarantee that the inscribed parallelogram is a square. Incorrect Response: C. Since the inscribed parallelogram must have right angles, the rhombus would have to be a square. Incorrect Response: D. The inscribed parallelogram must have right angles. The only kite that is a parallelogram with right angles is a square. |
|||||||||||||||||||||||||
| 52 | B |
Objective 010 Correct Response: B. In Triangle A B C , use Line segment A C as the base and draw height h from point B to Line segment A C or, in the case that angle A is obtuse, to the extension of base Line segment A C . Then Area equals one half times the length of segment A C times h The sine of A equals h over the length of segment A B, so h equals the length of segment A B times the sine of A Substituting for h in Area equals one half times the length of segment A C times h yields Area equals one half times length A B times length A C times the sine of A The sines of angles between 90 degrees and 180 degrees have the same values as their reference angles less than 90 degrees, so this formula is true for any triangle. Incorrect Response: A. The ratio is inverted. The sine of A equals h over length of the segment A B not The length of the segment A B over h Incorrect Response: C. While the formula is true for right triangles, it is also true for non-right triangles. Incorrect Response: D. The sines of angles between 90 degrees and 180 degrees have the same values as their reference angles less than 90 degrees, so this formula is true for any triangle. |
|||||||||||||||||||||||||
| 53 | B |
Objective 011 Correct Response: B. This net folds to create a rectangular pyramid whose vertex is above the point where the 12, 6, and 9 unit segments intersect—directly above one of the corners of its rectangular base. The base is a 12 by 6 rectangle, and the height is 9. The volume is One third of the product of 12 6 and 9 equals 216 cubic units. A rectangular pyramid with a base that is 12 units wide and 6 units deep. It is oriented so that the base and the edges of its width are parallel to the horizon. The edge that rises directly above the right rear corner of the base to the apex of the pyramid is 9 units tall. The line segment that extends from the apex and connects to the front right vertex of the base and has a length of the square root of 117 units. Incorrect Response: A. This response may be the result of using the right triangle whose legs measure 12 and the square root of 117 as the base of the pyramid and 6 as its height: one third times 12 divided by 2 times the square root of 117 end root times 6 equals 12 times the square root of 117 cubic units. Incorrect Response: C. This response may be the result of using the rectangle as the base, but incorrectly using 4 times 2 times one half times L times w as the height: one third times 12 times 6 times the square root of 117 equals 24 times the square root of 117 cubic units. Incorrect Response: D. This response may be the result of using the right triangle whose legs measure 12 and 9 as the base and 6 as the height and failing to recognize that the solid is a pyramid: 1 half times 12 times 9 times 6 equals 324 cubic units. |
|||||||||||||||||||||||||
| 54 | C |
Objective 011 Correct Response: C. A plane intersects a cube along the midline of its top face at an angle labeled 45 degrees and along the midline of its right face. The points of intersection along the top face are labeled A and B. This intersection forms two right triangles along the front and rear faces. The legs of these triangles are congruent The plane forms two pairs of parallel edges when it cuts through the top face of the cube at a 45 degree angle. The pair of edges formed along the top and right surfaces are congruent because they are both equal to the length of the cube. The pair of edges along the front and rear faces are also congruent. They can be thought of as the hypotenuses of the two isosceles right triangles, as shown in the diagram. Both pairs of adjacent sides are located within perpendicular planes (i.e., the adjacent faces of the cube) and so the angle of their intersection must be 90 degrees. The quadrilateral must be a rectangle because it has two pairs of congruent sides and four right angles. Incorrect Response: A. The quadrilateral is a parallelogram, but that is not its most descriptive name. Incorrect Response: B. Since adjacent sides of the quadrilateral are not equal, it cannot be a rhombus. Incorrect Response: D. Since adjacent sides of the quadrilateral are not equal, it cannot be a square. |
|||||||||||||||||||||||||
| 55 | D |
Objective 011 Correct Response: D. The plot can be divided into 2 right triangles similar to a 3 4 5 right triangle, one trapezoid, and a large triangle. Using ratios, the bases of the triangles similar to a 3 4 5 triangle are 15 yards and 12 yards. Between them is a trapezoid of height 21 yards and parallel bases 20 yards and 16 yards. The bottom triangle has base 48 yards and height 10 yards. The total area is One half times 15 times 20 plus one half times 21 times open paren 20 plus 16 close paren plus one half 12 times 16 plus one half times 48 times 10 equals 864 square yards. One square yard = 9 square feet, so 864 times 9 equals 7,776 square feet. Every 1000 square feet requires 3 pounds of seed, so 7,776 times 3 over 1,000 is approximately 23 point 3 pounds Incorrect Response: A. This response may be the result of calculating the area correctly as 864 square yards, but multiplying by 3 rather than 9 to convert to square feet. Incorrect Response: B. This response may be the result of calculating the areas of the triangles correctly, but miscalculating the area of the trapezoid, then multiplying by 3 rather than 9 to convert to square feet. Incorrect Response: C. This response may be the result of calculating the areas of the right triangles and the trapezoid correctly, but using the wrong base length for the bottom triangle. |
|||||||||||||||||||||||||
| 56 | A |
Objective 011 Correct Response: A. If the linear scale factor is k, then the original surface area S A will be multiplied by K squared and the original volume (V) by K cubed . The new ratio of surface area to volume will then be The ratio with numerator k squared times the surface area and denominator k cubed times the volume equals 1 divided by k times the ratio of the surface area to the volume equals 1 divided by k times r This response may also be found by setting up the formulas for surface area and volume for each cylinder and using algebraic properties to reduce the respective ratios. Incorrect Response: B. This response could be the result of simply assuming that the scale factor will apply to the efficiency ratio as well as to the linear dimensions. Incorrect Response: C. This response could be the result of understanding that the volume scale factor will be K cubed and misunderstanding the ratio components. Incorrect Response: D. This response could be the result of understanding that the volume scale factor will be K cubed and assuming that the original efficiency ratio will be multiplied by the volume scale factor. |
|||||||||||||||||||||||||
| 57 | D |
Objective 011 Correct Response: D. A cross-section of the cone along its axis showing where the frustum cut was made will contain similar right triangles. Let the slant height of the small cone that was cut off be x. Then X over the sum of x and 13 equals 4 over 9, X equals 10.4 and the slant height of the large cone is 23.4. Using the Pythagorean Theorem, 9 squared plus h squared equals 23 point 4 squared and h = 21.6. Incorrect Response: A. This response could be the result of using the incorrect proportion x over 13 equals 4 over 9, to get x is approximately 5.8 then 18.8 squared equals 9 squared plus h squared to get h = 16.5. Incorrect Response: B. This response could be the result of drawing the height of the frustum from the edge of the upper surface to find a 5, 12, 13 right triangle, so the height of the frustum is 12 units. Let y be the height of the small cone cut off. The incorrect proportion Y over 12 equals 4 over 9 yields y is approximately 5.3 , so the total height is 12 + 5.3 = 17.3. Incorrect Response: C. This response could be the result of using the incorrect proportion X over 13 equals 4 over 9 to get x is approximately 5.8 , then incorrectly setting up 18 point 8 squared plus 9 squared equals h squared to get h = 20.8. |
|||||||||||||||||||||||||
| 58 | D |
Objective 012 Correct Response: D. The equation provided describes a circle with a center of The coordinate 0 comma 4 and a radius of 5. Substituting 0 for x gives the y-intercepts for the circle: The equation open paren y minus 4 close paren squared equals 25 yields y minus 4 equals plus or minus 5. This yields y equals 4 plus or minus 5. The solutions to the equation are y equals 9 and y equals negative 1. The parabola intersects the y-axis in two places, so x is a function of y in its equation. The parabola will intersect 9 and negative 1 on the y-axis if it has factors The binomial y minus 9 times the binomial y plus 1 equals y squared minus 8 x minus 9. When y = 0, the parabola must have a value of 1, so The equation x equals a times open paren y squared minus 8 y minus 9 close paren yields the equation 1 equals a times open paren 0 squared minus 8 times 0 minus 9 close paren. This simplifies to the equation 1 equals negative 9 a. The value of a equals negative one ninth. This gives the equation X equals negative one ninth times open paren y squared minus 8 y minus 9 close paren. . Incorrect Response: A. This equation may be the result of assuming that the parabola must have the same x-intercepts as the circle provided. Incorrect Response: B. This equation is the result of the misconception that the parabola has x-intercepts that are the same as the y-intercepts for the circle provided. Incorrect Response: C. This equation may be the result of using the x-intercepts for the circle instead of the y-intercepts. |
|||||||||||||||||||||||||
| 59 | C |
Objective 012 Correct Response: C. It is necessary to find the center and semi-axis lengths of the ellipse. Use completing the square. The equation given can be rewritten as 4 times the trinomial x squared plus 4 x plus 4 is added to the product of 9 and the trinomial y squared minus 2 y plus 1. This equals 11 plus 16 plus 9 or 4 times open paren x plus 2 close paren squared plus 9 open paren y minus 1 close paren squared equals 36 Dividing by 36 yields One ninth times open paren x plus 2 close paren squared plus one fourth open paren y minus 1 close paren squared equals 1 The center of the ellipse is negative 2 comma 1 . The major axis is horizontal with half-length 3. The minor axis is vertical with half-length 2. The distance from the center to one focus is  or The square root of 5 .
The foci are located on the major axis of the ellipse. Thus, the foci are The square root of 5 units to the right and left of the center of the ellipse, at x-coordinates of negative 2 plus or minus The square root of 5
or The square root of 5 .
The foci are located on the major axis of the ellipse. Thus, the foci are The square root of 5 units to the right and left of the center of the ellipse, at x-coordinates of negative 2 plus or minus The square root of 5
Incorrect Response: A. This response is the result of calculating the distance from the center to one focus correctly, but placing the foci on the vertical axis rather than on the horizontal axis. Incorrect Response: B. This response is the result of calculating the distance from the center to one focus using 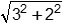 and then placing the foci on the vertical axis rather than on the horizontal axis. and then placing the foci on the vertical axis rather than on the horizontal axis.
Incorrect Response: D. This response is the result of calculating the distance from the center to one focus using 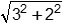 and then placing the foci on the horizontal axis. and then placing the foci on the horizontal axis.
|
|||||||||||||||||||||||||
| 60 | A |
Objective 012 Correct Response: A. The slope of segment A B is Rational expression with a numerator of 3 minus negative 7 and a denominator of 5 minus 1 equals 5 halves The slope of a line perpendicular to segment AB is the opposite reciprocal of 5 halves which is Negative 2 fifths The midpoint of segment A B is The coordinate of one half the sum of 5 plus 1 comma one half of the sum of 3 plus negative 7 or The coordinate 3 comma negative 2 Using point-slope form, the equation of the perpendicular bisector is Y plus 2 equals negative 2 fifths times open paren x minus 3 close paren or 2 x plus 5 y equals negative 4 Incorrect Response: B. This response may be the result of calculating the slope correctly but thinking that the midpoint is found using The coordinate of one half the difference of 5 and 1 comma one half of the difference of 3 and negative 7. This simplifies to the coordinate 2 comma 5 and not checking the validity of this result. The equation thus becomes Y minus 5 equals negative 2 fifths times open paren x minus 2 close paren or 2 x plus 5 y equals 29 Incorrect Response: C. This response may be the result of calculating the midpoint correctly but thinking that the slope of segment A B is Rational expression with a numerator of 5 minus 1 and a denominator of 3 minus negative 7 equals 2 fifths Then the negative reciprocal is negative 5 halves and the equation becomes Y plus 2 equals negative 5 halves times open paren x minus 3 close paren or 5 x plus 2 y equals 11 Incorrect Response: D. This response may be the result of calculating both the midpoint and the slope incorrectly. Using The coordinate 2 comma 5 and Negative 5 halves results in Y minus 5 equals negative 5 halves times open paren x minus 2 close paren or 5 x plus 2 y equals 20 |
|||||||||||||||||||||||||
| 61 | C |
Objective 012 Correct Response: C. Using segment BC as the base of triangle ABC, its height is the distance from Point A at coordinate negative 6 comma 8 to the line y = 2. That distance is 6. The base length is 5 minus negative 4 equals 9 . The area of triangle ABC is One half times 9 times 6 equals 27 Triangle A prime B prime C prime is similar to triangle ABC and has a scale factor of 4 thirds. The ratio of the area is the square of the fraction 4 thirds or 16 ninths. The area of triangle A prime B prime C prime is 16 ninths times(27) = 48. Incorrect Response: A. This response may be the result of calculating the area of triangle ABC correctly but using the scale factor rather than its square to find the area of triangle A prime B prime C prime : 27   times 4 thirds = 36. times 4 thirds = 36.
Incorrect Response: B. This response may be the result of calculating the height of triangle ABC incorrectly using the length of side A B equals the square root of the sum of 36 and 4 which simplifies to 2 times the square root of 10 The area becomes 9 times the square root of 10 and then is multiplied by the scale factor: 9 times the square root of 10 end root times 4 thirds equals 12 times the square root of 10 Incorrect Response: D. This response may be the result of calculating the height of triangle ABC incorrectly as in response B to get the area 9 times the square root of 10 then correctly using the square of the scale factor: 9 times the square root of 10 end root times the square of 4 thirds equals 16 times the square root of 10 |
|||||||||||||||||||||||||
| 62 | B |
Objective 012 Correct Response: B. This axiom still holds in spherical geometry. An example is shown below. A sphere is shown with two circles along its surface. The vertical angles formed by these circles are labeled congruent. Incorrect Response: A. This response is not true in spherical geometry; antipodal points like the north and south poles on a globe have many different routes between them that are of equal length. Incorrect Response: C. This statement is true for plane geometry, but it is not true in spherical geometry, as the sum of the interior angles in a triangle on a sphere can exceed 180 degrees. Incorrect Response: D. This is untrue in spherical geometry. For a given line and a point not on the line, many different lines (circles) can be drawn that contain the point and do not intersect the given line. |
|||||||||||||||||||||||||
| 63 | D |
Objective 012 Correct Response: D. A glide-reflection across Line segment A C is a combination of a reflection over Line segment A C followed by a translation parallel to Line segment A C . A reflection across the line A C produces the following result: A tread pattern for a tire is shown. The tread is in the shape of a thick line that zig zags in a wave pattern vertically. The vertical line segment A C passes through the midline of the wave pattern. Point B is on A C, located at the rightmost point on the tread when the shape of the tread is pointing to the left. An image of this is shown reflected over the line A B. It appears as if the original zig zag wave were vertically shifted by half of its wavelength. A subsequent translation up or down will produce the same pattern as the original image. Incorrect Response: A. A dilation produces an image that is similar to the original image, but changing the size produces two non-congruent shapes. Incorrect Response: B. A 180-degree rotation about point B produces the following result, which is not identical to the original image. 
Incorrect Response: C. A reflection across Line segment A C is shown in the rationale for response D. This transformation requires a translation to result in a congruent shape to the original. |
|||||||||||||||||||||||||
| 64 | C |
Objective 013 Correct Response: C. The digits 0 and 1 represent 20% of the single-digit numbers. Each single-digit number represents a box of crackers. Counting the number of single digits read until a 0 or 1 is read is the same as counting the number of boxes purchased until the desired coupon is found. The average number of boxes will be the average of the results of the 100 trials. Incorrect Response: A. This response does not model the problem. The number 20 is only one of 90 two-digit numbers. It does not represent 20% of the two-digit numbers. Incorrect Response: B. This response does not model the problem. Tossing the coins 10 times models buying 10 boxes, not asking how many boxes until a coupon is found. Incorrect Response: D. This response does not model the problem. Tossing a coin 5 times models buying 5 boxes, not asking how many boxes until a coupon is found. |
|||||||||||||||||||||||||
| 65 | B |
Objective 013 Correct Response: B. Since the numbers picked are real numbers, there are infinitely many pairs to consider. Use an area diagram to represent the situation. Consider a square drawn on a coordinate plane with vertices (1, 1), (1, 7), (7, 1), and (7, 7). Its area is 6 times 6 = 36. The number pair must satisfy the inequality X plus y is greater than or equal to 6 . This is the region in the square and above or on the line Y equals negative x plus 6 . This line intersects the sides of the square at (1, 5) and (5, 1). The area in the square and below Y equals negative x plus 6 is 1 half(4 times 4) = 8, so the area above this line is 36 minus 8 equals 28 . The probability that X plus y is greater than or equal to 6 is 28 over 36 or 7 ninths. Incorrect Response: A. This response satisfies the probability that X plus y is less than or equal to 6 . Incorrect Response: C. This response is the probability that X plus y is less than 6 if x and y are whole numbers. There will be 7 times 7 pairs and 10 pairs will have a sum less than 6. Incorrect Response: D. This response is the probability that X plus y is greater than or equal to 6 if x and y are whole numbers. There will be 7 times 7 pairs, and 39 pairs will have a sum greater than or equal to 6. |
|||||||||||||||||||||||||
| 66 | C |
Objective 013 Correct Response: C. There are 3 branches of the tree to consider: WW, WL, and LW. The probability of WW is One third times one fifth of WL is One third time 4 fifths and of LW is 2 thirds times 1 fifth The sum of these probabilities is 7 fifteenths Incorrect Response: A. This response considers only the branches that are labeled wins: 1 third times 1 fifth plus 1 fifth equals 4 fifteenths Incorrect Response: B. This response is the calculation for exactly one win: 1 third times 4 fifths plus 2 thirds times 1 fifth equals 2 fifths Incorrect Response: D. This response is the result of thinking that The probability of winning 2 games plus the probability of winning the first game plus the probability of winning the second game equals 1 third times 1 fifth plus 1 third plus 1 fifth equals 3 fifths |
|||||||||||||||||||||||||
| 67 | A |
Objective 013 Correct Response: A. The probability of a person winning on any particular day is 1 over 150 For the entire week, the expected value of winning is The sum of 40 50 20 20 20 50 and 100 divided by 150 equals 2 dollars. For Friday and Saturday, the expected value of winning is The sum of 50 and 100 divided by 150 equals 1 dollar Thus, the difference is 1 dollar . Incorrect Response: B. This response is the expected value of winnings for the entire week. Incorrect Response: C. This response is the difference between the winning amounts on Friday and Sunday. Incorrect Response: D. This response is the sum of the winnings for the week minus the sum of the winnings through Thursday. |
|||||||||||||||||||||||||
| 68 | D |
Objective 014 Correct Response: D. This sampling method is similar to stratified random sampling. This method ensures that caregivers at each school have an opportunity to be included in the sample. Calling non-respondents from this sample should increase the response rate and make it more representative of the overall population. This method is most effective when all 30 caregivers respond and the number of caregivers at each school is equal. Incorrect Response: A. This is an attempted census. The non-response rate will contribute to a bias. Those who do respond may have a different opinion than those who do not. Incorrect Response: B. This is cluster sampling. The opinions of the parents or guardians from one school may not be representative of the opinions of those from the other schools. Incorrect Response: C. This asks for a voluntary response from those who have access to a computer. Only those who have internet and feel strongly will respond. |
|||||||||||||||||||||||||
| 69 | B |
Objective 014 Correct Response: B. A box-and-whisker plot displays the lowest value, first quartile value, median, third quartile value, and highest value of a data set. The stem-and-leaf plot already orders the data. Since there are 25 values, the median is the thirteenth value, which is 25. The first quartile value is the median of the lowest 12 values, or 12. The third quartile value is the median of the highest 12 values, or 28. The first whisker extends from 2 to 12. The box extends from 12 to 28 with a vertical segment at 25. The last whisker extends from 28 to 34. Thus, B is the correct box plot. Incorrect Response: A. This response has the correct median, but incorrect first and third quartile values. It appears that the value occurring the most often in the first 12 and last 12 data were used rather than the quartile values for the ends of the box. Incorrect Response: C. This response marks the median as 20, which is the mean of the data. It appears that the first and third quartiles are correct. Incorrect Response: D. This response marks the median as 20, which is the mean of the data. It appears that the value occurring the most often in the first 12 and last 12 data were used rather than the quartile values for the ends of the box. |
|||||||||||||||||||||||||
| 70 | B |
Objective 014 Correct Response: B. Doubling the values of the data set results in a horizontal dilation of the x-axis, stretching the shape of the distribution wider. The mean and median are measures of center in a data set. These measures will double when the values double. Incorrect Response: A. The median describes the center of a sorted data set, so if a data set is doubled, the median is doubled as well. Doubling the values of the data set results in a horizontal dilation of the x-axis, stretching the shape of the distribution wider. Incorrect Response: C. The mean describes the average value in a data set: x bar equals the sum of quotient of x sub i and n taken from i equals 1 to i equals n If a data set is doubled, the median is doubled as well: the sum of the quotient of 2 x sub i and n taken from i equals 1 to i equals n is equivalent to 2 times the sum of the quotient of x sub i and n taken from i equals 1 to i equals n. These expressions are equal to 2 times x bar. Doubling the values of the data set dilates the values on the x-axis by a factor of 2, so the shape of the new data distribution will be twice as wide as the original shape. Incorrect Response: D. This conclusion is only true in the case where both the mean and the median of the original data set are equal to 0. |
|||||||||||||||||||||||||
| 71 | A |
Objective 014 Correct Response: A. The value r is the correlation between the y-values predicted by the regression equation and the observed values for y. Since the r value for Town A is greater than the r value for Town B, the regression equation for Town A is a better predictor of y-values (population) than the equation for Town B. Incorrect Response: B. This conclusion stems from the misconception that the y-intercept of both equations (the b value) indicates the initial population for each town. The actual population for either town could have been greater or less than the value predicted by the linear regression, so this conclusion cannot be reached from the information provided. Incorrect Response: C. The growth rate, a, indicates that the population of Town A is increasing at a rate of Approximately 0 point 47 times 1,000 equals 470 people per year, while the rate of change for Town B is an additional Approximately 3 point 86 times 1,000 equals 3,860 people per year. Incorrect Response: D. The students have created a linear model of the data, meaning that a "line of best fit" was calculated from the data. The provided information offers insight only into the parameters of the line and the extent to which the populations of the two towns exhibit a linear association. Acceleration and deceleration are concepts that involve varying rates of change, which is information not captured by the output of linear regression model. |
|||||||||||||||||||||||||
| 72 | A |
Objective 015 Correct Response: A. Since direct substitution leads to the indeterminate form 0 divided by 0, it is necessary to rewrite The limit of the rational expression with a numerator of 1 minus x and a denominator of x squared minus 1 as x goes to 1 as The limit of the rational expression with a numerator of negative 1 times the binomial x minus 1 and a denominator of the binomial x plus 1 times the binomial x minus 1 as x goes to 1. For x is not equal to 1, this expression is equivalent to The limit of the rational expression with a numerator of negative 1 and a denominator of x plus 1 as x goes to 1. For x values close to 1, rational expression with a numerator of negative 1 and a denominator of x plus 1 is close to negative 1 half, thus The limit of the rational expression with a numerator of 1 minus x and a denominator of x squared minus 1 as x goes to 1 equals negative one half Incorrect Response: B. This response could be the result of thinking that 0 divided by 0 = 0. Incorrect Response: C. This response could be the result of thinking that 0 divided by 0 = 1. Incorrect Response: D. This response could be the result of thinking that since 0 divided by 0 is indeterminate, the limit does not exist. |
|||||||||||||||||||||||||
| 73 | A |
Objective 015 Correct Response: A. The slope of the tangent line at x = 1 is found by evaluating the derivative of the function for x = 1. Using the chain rule, The derivative of y with respect to x equals one half times open paren x squared plus 1 close paren exponent negative one half times 2 x For x = 1, The derivative of y with respect to x equals the square root of 2 end root over 2 and 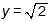 , so the equation of the tangent line is
Y minus the square root of 2 equals the square root of 2 end root over 2 times the binomial x minus 1
or
Y equals the square root of 2 end root over 2 times x plus the square root of 2 end root over 2 , so the equation of the tangent line is
Y minus the square root of 2 equals the square root of 2 end root over 2 times the binomial x minus 1
or
Y equals the square root of 2 end root over 2 times x plus the square root of 2 end root over 2
Incorrect Response: B. This response could be the result of neglecting to use the chain rule so The derivative of y with respect to x equals one half times open paren x squared plus 1 close paren exponent negative one half and  is used as the slope of the line. is used as the slope of the line.
Incorrect Response: C. This response could be the result of correctly finding the derivative and the slope but using x + 1 instead of x minus 1 in the point-slope form of the line. Incorrect Response: D. This response could be the result of both neglecting to use the chain rule and using x + 1 instead of x minus 1 in the point-slope form of the line. |
|||||||||||||||||||||||||
| 74 | B |
Objective 015 Correct Response: B. The radius expands at a rate of 9 inches per second, which is equivalent to a rate of 0.75 feet per second. The function A of t equals pi times the square of the function r of t describes how the area of this circle changes over time. The rate at which the area changes is equal to A prime of t equals 2 pi times r of t times r prime of t equals 2 pi times 0 point 75 times t times 0 point 7 5 At 2 seconds, A prime of 2 equals 7 point 1 feet per second. Incorrect Response: A. This response represents the radius of the circular ripple in feet per second at t = 2 seconds. Incorrect Response: C. An incorrect application of the chain rule may lead to this result. If the derivative is taken to be A prime of t equals 2 pi times 0 point 7 5 times t then A prime of 2 equals 2 pi times 0 point 75 times 2 and this is approximately equal to 9 point 4 Incorrect Response: D. An incorrect derivative may lead to this result. If the derivative is taken to be A prime of t equals 2 pi times 2 times 0 point 7 5 times t then A prime of 2 is approximately equal to 18 point 9 |
|||||||||||||||||||||||||
| 75 | C |
Objective 015 Correct Response: C. A function is continuous for all real numbers if no real numbers are excluded from the domain of f of x and the values of the function transition smoothly at every point (i.e., there are no jumps, vertical asymptotes, or point discontinuities—the limit of the function is defined at and around every real number value). The functions x squared + 2 and x + 2 are both continuous. Crucially, both functions return the same value for x = 1, and the piecewise function f of x transitions smoothly for a given interval around this point. Incorrect Response: A. This rational function simplifies to F of x equals a rational expression with a numerator of x squared minus 9 and a denominator of x minus 3. The numerator factors into the binomials x plus 3 and x minus 3. The factors of x minus 3 cancel and the result is x plus 3. but this function has a point discontinuity at x = 3. This function is not continuous because this value is excluded from its domain. Incorrect Response: B. This function is not defined for x is less than 3. Incorrect Response: D. The graph of this function jumps at the point x = 1. At x = 1, f of 1 = 1 + 2 = 3. At x = 1 + epsilon , where epsilon is a small positive number, f of argument 1 plus epsilon end argument equals 1 plus epsilon minus 2 equals negative 1 plus epsilon |
|||||||||||||||||||||||||
| 76 | A |
Objective 015 Correct Response: A. If a of x equals x to the fifth power and b of x equals 2 times x exponent 4 plus 3 then f of x equals a of b of x By the chain rule, the derivative of f of x equals a prime of b of x times b prime of x That is, the derivative is first applied to the function a of x and then x is substituted with 2 times x exponent 4 + 3. This quantity is then multiplied by b prime of x : F prime of x equals 5 times open paren 2 times x exponent 4 plus 3 close paren exponent 4 times the derivative of 2 times x exponent 4 plus 3 with respect to x. This equals 5 times open paren 2 times x exponent 4 plus 3 close paren exponent 4 times 4 times 2 times x cubed Incorrect Response: B. This response could be the result of misapplying the chain rule. In this case, the derivative for 2 times x exponent 4 multiplies the original function. Incorrect Response: C. This response does not apply the chain rule. Incorrect Response: D. This response applies the derivative directly to the term 2 times x exponent 4 . |
|||||||||||||||||||||||||
| 77 | D |
Objective 016 Correct Response: D. The function G of x =  represents net area between the graph of f and the x-axis over intervals from negative 4 to values of x in
Open bracket negative six comma 6 close bracket . Since
The integral of f of t d t over the interval from t equals negative 4 to negative 6 has the opposite value of the same integral taken over the interval from negative 6 to negative 4,
the integral is positive even though the function is negative for these values of t.
G of negative 6 = 3. (This value is computed geometrically by finding the area of a triangle with a height of 3 and a base of 2.) The value of the integral decreases as x increases toward negative 4 until it becomes
G of negative 4 = 0.
represents net area between the graph of f and the x-axis over intervals from negative 4 to values of x in
Open bracket negative six comma 6 close bracket . Since
The integral of f of t d t over the interval from t equals negative 4 to negative 6 has the opposite value of the same integral taken over the interval from negative 6 to negative 4,
the integral is positive even though the function is negative for these values of t.
G of negative 6 = 3. (This value is computed geometrically by finding the area of a triangle with a height of 3 and a base of 2.) The value of the integral decreases as x increases toward negative 4 until it becomes
G of negative 4 = 0. G of x increases as x increases from negative 4 to 0 until it becomes G of 0 = 4. To the right of this point, the area of the semicircle will be subtracted since it is below the x-axis, so G of x will decrease as x increases from 0 to 4 until it becomes G of 4 = 4 minus 2π. For x > 4, area is above the x-axis and added, so G of x will increase. Thus G of x achieves its minimum value when x = 4. Incorrect Response: A. This response could result from thinking that the minimum value of f will also result in the minimum value of G. Incorrect Response: B. This response could result from reasoning that G of negative 6 = 3 and G of negative 4 = 0, then reasoning that for x greater than negative 4, the area will increase. Incorrect Response: C. This response could result from recognizing that f has a local minimum at x = 2 and thinking that G will have a minimum there also. |
|||||||||||||||||||||||||
| 78 | C |
Objective 016 Correct Response: C. Let u = x cubed + 1 so that d u equals 3 times x squared d x and x squared d x equals 1 third d u This substitution changes the limits of the integral. For x = 0, u = 1 and for x = 1, u = 2. Substituting, the integral of x squared times begin square root x cubed plus 1 end root d x over the interval from 0 to 1 equals one third times the integral of u exponent one half d u taken over the interval from 1 to 2. Integration yields The change in the expression 2 ninths u exponent three halves from u equals 1 to u equals 2 is equal to 2 ninths times open paren 2 times the square root of 2 end root minus 1 close paren Incorrect Response: A. This response is the result of substituting the variables correctly but forgetting to change the limits of integration: One third times the integral of u exponent one half d u taken over the interval from 0 to 1 equals two ninths Incorrect Response: B. This response is the result of forgetting the one third when substituting and forgetting to change the limits of integration: The integral of u exponent one half d u taken over the interval from 0 to 1 equals two thirds Incorrect Response: D. This response is the result of remembering to change the limits of integration, but forgetting the 1 third when substituting: The integral of u exponent one half evaluated from u equals 1 to u equals 2 is equal to two thirds times open paren 2 times the square root of 2 end root minus 1 close paren |
|||||||||||||||||||||||||
| 79 | B |
Objective 016 Correct Response: B. Simplify: The integral of rational expression with a numerator of x squared minus 5 and a denominator of x squared d x is equal to the integral of x squared divided by x squared minus 5 over x squared d x. This may be written as the integral of open paren 1 minus 5 x exponent negative 2 close paren d x. The antiderivative is x minus 5 times open paren the fraction with numerator x exponent negative 1 and denominator negative 1 close paren plus C is equal to x plus 5 over x plus C Incorrect Response: A. This response could be the result of simplifying correctly to get the integral of open paren 1 minus 5 x exponent negative 2 close paren dx but not recognizing that the antiderivative of 1dx is x. Incorrect Response: C. This response could be the result of not simplifying and taking the antiderivatives of the numerator and denominator independently to get the rational expression with a numerator of x cubed divided by 3 minus 5 x and a denominator of x cubed divided by 3 plus C equals 1 minus 15 over x squared plus C. Incorrect Response: D. This response could be the result of simplifying to get 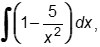 , but, for the fraction, taking the antiderivatives of the numerator and denominator independently to get
x minus rational expression with a numerator of 5 x and a denominator of x cubed divided by 3 plus C equals x minus 15 over x squared plus C , but, for the fraction, taking the antiderivatives of the numerator and denominator independently to get
x minus rational expression with a numerator of 5 x and a denominator of x cubed divided by 3 plus C equals x minus 15 over x squared plus C
|
|||||||||||||||||||||||||
| 80 | A |
Objective 016 Correct Response: A. The function h = x times the binomial 12 minus x has x-intercepts at x = 0 and 12. The area between the curve and the x-axis is found by evaluating an integral The integral of open paren 12 x minus x squared close paren d x equals the change in the expression 6 times x squared minus x cubed over 3 from x equals 0 to x equals 12. This is equal to 6 times 144 minus 576, which is 288. Incorrect Response: B. This response could be the result of estimating the area using the formula for the area of an ellipse: One half times pi times 6 times 36 is approximately equal to 339 Incorrect Response: C. This response could be the result of integrating correctly, but making an error by evaluating 6 times x squared as 72 squared, so 72 squared minus 576 equals 4,608 Incorrect Response: D. This response could be the result of integrating each factor to get The change in the expression open paren x squared divided by 2 times the binomial 12 x minus x squared over 2 close paren from x equals 0 to x equals 12 is equal to 72 times 72, which is 5,184 . |
|||||||||||||||||||||||||
| 81 | B |
Objective 016 Correct Response: B. A continuous function is used to describe the rate at which the capacity of the water treatment plant is growing. The total capacity (i.e., the total water treated) at the end of five years is the integral of the capacity rate The integral of c of t d t equals the integral of 1 point 2 e begin superscript 0 point 1 4 times t end superscript d t taken over the interval from 0 to 5. This evaluates as 1.2 times 1 over 0.14 times the change in the expression e begin superscript 0.14 times t end superscript from t = 0 to t = 5. This equals 8.57 times open paren e begin superscript 0.14 times 5 end superscript minus e exponent 0 close paren, which is about 8.7 million gallons. Incorrect Response: A. This is c of 5 , which represents the millions of gallons per year that the water treatment plant will treat at the beginning of its fifth year. Incorrect Response: C. This represents c of 1 + c of 2 + c of 3 + c of 4 + c of 5 , the sum of the capacity rates at the end of each year. This overestimates the total amount of water treated because it applies the year end capacity rate to the entire year. In contrast, the provided information describes a gradual increase in capacity rate from the beginning to the end of the year. For example, c of 0 = 1.2 million gallons per year, c of 1 = 1.38 million gallons per year, and these rates are connected by a continuous exponential function. Incorrect Response: D. If the lower bound of the integral were ignored such that The integral of c of t d t equals the integral of 1 point 2 e begin superscript 0 point 1 4 times t end superscript d t. This is equal to 1 point 2 times 1 over 0 point 1 4 times e begin superscript 0 point 1 4 times t end superscript then the result at t = 5 is 8.57 times e begin superscript 0 point 1 4 times 5 end superscript which is about 17.3 million gallons. |
|||||||||||||||||||||||||
| 82 | D |
Objective 017 Correct Response: D. The student must now show that the equation is true for k + 1 odd numbers. If there are k + 1 odd numbers, the last odd will have a value of 2 open paren k + 1 closed paren minus 1 or 2 k plus 1 If the sum of k odd numbers is K squared then the sum of k + 1 odd numbers must be The square of the binomial k plus 1 . Thus, the student must show that The sum of 1 + 3 + 5 + 7 + and so on up to open paren 2 times k minus 1 close paren + open paren 2 k + 1 close paren = the square of the binomial k + 1 Incorrect Response: A. This response may be the result of thinking that "the next" means add 1 to the "last," so 1 is added on each side of the equation. Incorrect Response: B. This response may be the result of thinking that "the next" means add 1 to the "last," so 1 is added on the left, but the k + 1 is substituted correctly on the right. Incorrect Response: C. This response uses the correct expression for the next odd number on the left, but misinterprets The square of the binomial k plus 1 as K squared plus 1 |
|||||||||||||||||||||||||
| 83 | C |
Objective 017 Correct Response: C. According to the entries in the first row, communication goes from computer A to computers B, C, and E. Thus, the directed graph has arrows from A to B, C, and E. The entries in row 2 correspond to arrows going from B to A and D. The 1 in row 3 corresponds to an arrow from C to B. From rows 4 and 5, the ones correspond to arrows from D to A and C, and from E to A. The graph in response C shows all these. Incorrect Response: A. This response misinterprets connections, assuming, for example, that going from A to B is the same as going from B to A. Incorrect Response: B. This response misinterprets connections as in response A, but also reads the information down the columns rather than across the rows. Incorrect Response: D. This response reverses the expected connections. The rows of the matrix establish the origin of the connection and the columns describe their destination. This may be the result of reading down the columns of the matrix rather than across the rows. |
|||||||||||||||||||||||||
| 84 | C |
Objective 017 Correct Response: C. The equations x + y + 35 = 49, y + z + 27 = 48, and x + z + 31 = 50 follow from the information provided. Solving simultaneous equations yields x = 6, y = 8, and z = 13. The total number of students who played sports is 24 + 20 + 16 + 6 + 8 + 13 + 11 = 98. Then 212 minus 98 = 114 students who played no sports. Incorrect Response: A. This response may be the result of subtracting the sum of 50, 49, and 48 from 212. It does not take overlaps into account. Incorrect Response: B. This response may be the result of subtracting the sum of 50, 49, and 48 from 212, but then adding back the 11 twice since it was counted in each of the three amounts subtracted. Incorrect Response: D. This response may be the result of adding 50, 49, and 48, then subtracting the sum of the overlaps of 11, 20, 24, and 16. The result, 76, is then subtracted from 212. |
|||||||||||||||||||||||||
| 85 | B |
Objective 017 Correct Response: B. There are 12 factorial ways to arrange 12 visitors in 12 positions and 2 factorial ways to arrange the 2 naturalists in 2 positions. By the fundamental counting principle, there are 2 factorial times 12 factorial equals 2 times 12 factorial different orders in which the group may be arranged. Incorrect Response: A. This response represents the number of ways to arrange the visitors. However, any order for the visitors may be combined with 2 possible ways to arrange the naturalists, so this represents half of the total number of arrangements. Incorrect Response: C. This response describes how many ways that a group of 14 people may be arranged into a single file line. This value is too large because it counts arrangements for which the naturalists can be located in the middle of the line and visitors at the end of the line. Incorrect Response: D. This response combines the misconception described in response C with the application of fundamental counting principle described in response B. |
|||||||||||||||||||||||||
| Total Correct: | Review your results against the test objectives. | ||||||||||||||||||||||||||
Open Responses, Sample Responses, and Analyses
| Question Number |
Your Response Read about how your responses are scored and how to evaluate your practice responses |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 86 |
Open Response Item Assignment #1 For each assignment, you may type your written response on the assigned topic in the box provided. Note: The actual test allows you to handwrite your responses on separate response sheets to be scanned for upload to the test. For this practice test, you may handwrite each response on 1–2 sheets of paper. |
||||||||||
| First Sample Weak Response |
First Sample Weak Response to Open-Response Item Assignment #1
Part 1:
3 concentric circles are shown. The radius of the inner circle is labeled r. The area within this circle is shaded. The distance between the boundary of the first circle and the boundary of the second circle is labeled r. This area is unshaded. The distance between the boundary of the second circle and the boundary of the third circle is also labeled r. This area is shaded. Part 2 A simple sketch of a graph and a table are shown. The graph shows the coordinate plane with 4 quadrants. A curve is drawn from the origin that curves upward in a manner similar how a parabola would increase: increasing slowly at first and more quickly further from the origin. The table has two columns. The column labeled R has values 1, 2, and 3. The column labeled A has values 6 pi, 24 pi, and 54 pi. Part 3: The equation 6 pi r squared equals 150 pi is simplified as r squared equals 25. Part 4: An equation is shown above a ratio. The equation reads 4 pi r squared plus 9 pi r squared minus 4 pi r squared equals 9 pi r squared. The ratio has numerator of 6 pi r squared divided and a denominator of 9 pi r squared. |
||||||||||
| First Weak Response Analysis |
Analysis of First Weak Response to Open-Response Item Assignment #1 Purpose: All parts of the assignment are attempted but only partially achieved. For example, Part 1 is correctly solved but lacks supporting detail, explanation, and steps to reach the solution. In Part 3, the candidate attempts to address the task but does not complete it. In Part 4, it is unclear how the equation presented would find how the area of the shaded regions would change when the radius of the innermost circle is doubled. Subject Matter Knowledge: The candidate shows a limited understanding of what the task requires. For instance, in Part 1, the candidate uses a viable method and arrives at a correct answer, but without showing their work, there is insufficient evidence of understanding. Part 2 has a correct table of values but does not indicate how those values were obtained, such as defining the formula used to calculate A in terms of R. Additionally, the graph lacks labeled axes and defined coordinates. Part 3 correctly sets up a viable equation but does not solve it to completion to respond to the question being asked. In Part 4, the logic used is not explained and seems to reflect inaccurate subject matter knowledge. Support: Support is limited throughout the response. The candidate does not show or explain all the steps involved in solving the problem. Including intermediate steps would help to clarify the candidate's approach to the problem. Rationale: The candidate does not provide enough explanation to logically convey the reasoning behind the attempt to solve the problem. The reasoning provided is limited. For example, in Part 1, the candidate provides the final equation with no justification for the reasoning needed to reach this point in the solution. Additionally, in Part 4, it is unclear how the candidate is interpreting the prompt. This lack of clear analysis to find the solution is a problem throughout the response, resulting in large gaps in logic that ultimately make the response poorly reasoned. |
||||||||||
| Second Sample Weak Response |
Second Sample Weak Response to Open-Response Item Assignment #1
Part 1:
3 concentric circles are shown. The radius of the inner circle is labeled r. The area within this circle is shaded. The distance between the boundary of the first circle and the boundary of the second circle is labeled r. This area is unshaded. The distance between the boundary of the second circle and the boundary of the third circle is also labeled r. This area is shaded. Part 2 A simple sketch of a graph and a table are shown. The graph shows the coordinate plane with 4 quadrants. A curve drawn from the origin curves upward in a manner that increases slowly at first and then more quickly as it moves to the right of the origin. Part 3 A hand drawn equation is solved over several steps. The first equation reads 9 times pi times r squared 2 equals 150 pi. The equation simplifies to 9 r squared equals 150 and then r squared equals 150 over 9. This becomes r equals the square root of 150 over 9 end root, which taken to be equivalent to 5 thirds times the square root of 6. Part 4 A hand drawn solution is shown over 3 lines. Line 1 reads: Area in middle with r doubled is pi times open paren 2 r close paren squared equals 4 pi r squared, Line 2 reads: 16 pi r squared minus 9 pi r squared plus 4 times pi times r squared equals 11 pi r squared. Line 3 reads: so area increased by 5 pi times r squared. A note indicates this is came from 11 pi r squared minus 6 pi r squared. |
||||||||||
| Second Weak Response Analysis |
Analysis of Second Weak Response to Open-Response Item Assignment #1 Purpose: The purpose is partially achieved. The candidate attempts to address all the components of the prompt. In Part 1, when analyzing the shaded part, each circle's area is found, and the correct process is used to find the shaded region. In Part 2, a sketch of the graph does not include all appropriate labels. The variables on the axes are not defined, and no units are given to enable reading of the graph, though the general shape of the graph shows some understanding of graphs of quadratic functions. There is no explanation of the meaning of any intercepts or extrema in the context of this situation. In Part 3, a quadratic equation is solved for x but there is a mistake in the original setup using 9 pi r squared instead of 6 pi r squared . In Part 4, the candidate misinterprets the meaning of "double the r in the innermost circle" to mean that only the small circle gets a new radius of 2r when in this problem all r's should become 2r. The response shows a lack of understanding of the meaning of ratio. Subject Matter Knowledge: The candidate is able to utilize the correct formula for calculating the area of a circle, graphs a quadratic equation, and solves a quadratic equation. While the graph is labeled by the variables, intercepts and extrema were not labeled or explained. The candidate knows the formula for a circle and analyzes the diagram to find the shaded region correctly. In Part 3, the candidate incorrectly uses the largest circle in the calculation instead of the shaded area, but exhibits the ability to solve a quadratic equation given the context of the problem (positive solutions). In Part 4, the candidate does not realize that every r in the diagram should be doubled, which leads to the wrong area. The candidate does not recognize that describing the change in the areas of the shaded regions would be best represented as a multiplicative relationship that should use ratio instead of the difference in those areas. Support: The support for this solution is limited. The response to Part 1 has reasonable support showing what the area of each circle and how they are added or subtracted to find the final area of the shaded region, but some explanation would have made it easier to follow and understand. In Part 2, there is insufficient evidence for interpreting this graph given the scenario. For Part 3, the 150 pi represents the shaded area; however, it is compared to the entire area of the largest circle as opposed to the shaded area found in Part 1. Without explanation of why 9 pi r squared was used, there is no way to know the reason for this error. In Part 4, the candidate takes the words "double the innermost r" to mean that 2r applies to the small circle only instead of understanding that every r now is 2r. Rationale: The response reflects limited reasoning. Even though the candidate analyzes the first part of the prompt correctly, many other errors occur. In Part 1, by finding the areas of large, middle, and small circle, the candidate analyzes the situation, explains what is happening and finds the formula. In Part 2, the graph is drawn but without identifying key features in the graph, it is unclear if its connection to the scenario is fully realized. In Part 3, it is not clear why the area of the largest circle is used instead of the shaded area in the equation to solve for the new r. In Part 4, the candidate misinterprets what double r means and does not recognize that a ratio would be a more appropriate measure of describing this change. More explanation of the reasoning used would strengthen this response. |
||||||||||
| First Sample Strong Response |
First Sample Strong Response to Open-Response Item Assignment #1 3 concentric circles are shown. The radius of the inner circle is labeled r. The area within this circle is shaded. The distance between the boundary of the first circle and the boundary of the second circle is labeled r. This area is unshaded. The distance between the boundary of the second circle and the boundary of the third circle is also labeled r. This area is shaded. An arrow labeled center points to the circumference of the inner circle. An arrow labeled ring points to the circumference of the outermost circle.
The shaded area is composed of 2 shapes. Part 1 is a "ring" and part 2 is a circle (center). 2 Graph of f of x equals 6 times r squared times pi A graph and a table are shown. The graph has a vertical axis labeled shaded axis, y, and a horizontal axis labeled radius, r. The points 0 0, 1 6 pi, and 2 24 pi are shown in the graph. These points are connected by a parabola-shaped curve. The same points are shown in the following table.
Since this problem is representing area, the graph is only defined in the first quadrant. The y-intercept is The coordinate 0 0 which is a circle with radius = 0 so it is just a point—no area.
3 If shaded region is 150 pi , find radius 4 If original radius doubled, then small circle area is Open paren 2 times r close paren squared times pi. . Ring is Open paren 6 times r close paren squared times pi minus Open paren 4 times r close paren squared times pi equals 36 times r squared times pi minus 16 times r squared times pi equals 20 times r squared times pi. . Shaded is 4 times r squared times pi plus 20 times r squared times pi equals 24 r squared pi . It is 4 times the original. Rational expression with a numerator of 24 times r squared times pi and a denominator of 6 times r squared times pi equals 4. |
||||||||||
| First Strong Response Analysis |
Analysis of First Strong Response to Open-Response Item Assignment #1 Purpose: The candidate fully achieves the purpose of the assignment. All components of the question are fully addressed. The candidate's work is shown in detail as well as the reasoning for analyzing and solving the problem in the chosen approach. Subject Matter Knowledge: The candidate demonstrates substantial, accurate and appropriate subject matter knowledge. For example, the candidate selects the correct formulas and solves each formula accurately. Additionally, the candidate demonstrates knowledge of how to graph quadratic equations. The candidate also recognizes what happens when the radius is doubled and accurately represents the change in the area. Support: The candidate provides high-quality, relevant examples. For instance, when the area of the different circles was calculated, work is shown to justify the solution. Also, when an equation needs a solution, all the required steps are shown. The graph's axes are labeled and a table of values is shown, which aids in understanding of the graph. Rationale: The response shows comprehensive reasoning. For example, in Part 1, rather than simply providing the equation, the candidate demonstrates understanding of the relationship between the area of the three circles and how they affect the shaded region. Additionally, it is clear how the answers are derived in a clear and logical manner. In Part 1, the candidate explains how they are approaching the problem, labeling Part 1 as a ring and Part 2 as a circle. The candidate provides an outline of how they will solve the problem and follows through clearly, using the terms (ring, circle) that they have defined previously to explain their reasoning. Sound reasoning is further demonstrated in Part 2, where the candidate explains why the graph is only defined in the first quadrant. |
||||||||||
| Second Sample Strong Response |
Second Sample Strong Response to Open-Response Item Assignment #1
1 See diagram.
For the formula of the shaded region, take the area of the smaller circle then the area of the larger circle minus the second circle.
2 See graph
Intercept at The coordinate 0 0 represents a point.
3 If Area = 150 then substitute into formula A equals 6 pi times r squared 4 If r is doubled, then radius of the first circle (innermost circle) equals 2r, the next circle is 4r and the third circle (outermost circle) is 6r. A equals 4 pi times r squared plus 36 pi times r squared minus 16 pi times r squared. This simplifies to 24 pi times r squared.
Compare 6 pi times r squared to
24 pi times r squared |
||||||||||
| Second Strong Response Analysis |
Analysis of Second Strong Response to Open-Response Item Assignment #1 Purpose: The candidate has fully achieved the purpose of the assignment by finding the formula in Part 1, graphing the formula, adding appropriate labels, and explaining the meaning of intercepts in Part 2, finding the radius of the innermost circle in Part 3, and finding how the relationship to the area would change if the radius were doubled in Part 4. Subject Matter Knowledge: The answers are accurate and use the correct equations and algebraic reasoning. The graphing is built on a table using the appropriate equations, and the graph is only drawn in the first quadrant, where it is meaningful. The candidate also demonstrates understanding of how to find the area where the radius is doubled and compare the new area with the original area. Taken as a whole, the response demonstrates substantial subject matter knowledge. Support: The candidate provides sound supporting evidence throughout the response by showing how they find appropriate answers to the problem. The candidate also shows their reasoning to find the shaded area through the multi-step process that was required. All the steps necessary to answer the questions are shown in a linear and clear-cut fashion. Rationale: The response is ably reasoned. For instance, in Part 1, the candidate shows how the answer was derived from the given information in a three-step process. In the graphing in Part 2, the candidate justifies the graph by creating a table based on the formula derived. In Part 3, the candidate explains how to find the radius given a specific area, and in Part 4, the candidate not only gives the correct answer, but explains how they reached the answer. |
||||||||||
| 87 |
Open-Response Item Assignment #2 For each assignment, you may type your written response on the assigned topic in the box provided. Note: The actual test allows you to handwrite your responses on separate response sheets to be scanned for upload to the test. For this practice test, you may handwrite each response on 1–2 sheets of paper. |
||||||||||
| First Sample Weak Response |
First Sample Weak Response to Open-Response Item Assignment #2 The water loss from week 1 to week 5 is 109 minus 84 which is 25 inches over the 5 weeks, so the rate is 25 divided by 5 = 5 inches per week. Divide the starting water level of 109 by 5 to get 21.8 weeks from May 18. Since only 20 weeks are troublesome (up until the beginning of October), we have enough water to last until the beginning of October and then for another week. The water level should be always between 68 inches and 5 inches. Going down to no water is not healthy. The rate of water loss could be found using a larger range of values. Instead of the first 5 values, using the first 10 could get a better rate. Knowing the actual weather patterns in the area would make better predictions. A graph displays data from the stimulus plotted correctly and connected by a curve that bends as it passes through each of its points. The y axis is labeled water level and the x axis is labeled weeks. The vertical axis has a range from 60 to 110, with every 2 units representing a change of 10. The value of 60 is located 2 units above the original. Every other vertical unit is labeled with its corresponding water level. The horizontal axis has a range from 1 to 10, and every 1 unit represents 1 week. All 10 weeks are labeled. |
||||||||||
| First Weak Response Analysis |
Analysis of First Weak Response to Open-Response Item Assignment #2 Purpose: While all parts of the problem are addressed, they are not all answered completely, so the purpose is only partially achieved. A graph is drawn, and a rate of water loss is found. The candidate predicts when the water source would be empty if no outside water is added and gives some explanation for why the prediction may be faulty. Subject Matter Knowledge: There is a limited application of subject matter knowledge. Part 1 has a relatively good graph but needs the axes better defined. Units should be clearly stated. In Part 2, the candidate does find a rate of water loss accurately, but no explanation is given as to why that range was chosen. Assumptions made by the candidate are never stated or explained. The candidate never shows an understanding that water is added at some point and how that affects the prediction. There is no analysis of how the loss of water is increasing over the first 5 weeks; the rate found by the candidate is not realistic. The approach to find out when the reservoir would be empty is faulty due to the choice of rate and never considers water being added in week 5. In Part 3, a range of water heights is given but with little justification or rationale for those choices. In Part 4, two factors are given but no discussion about why they will influence the prediction. Support: Support is somewhat limited. The graph does show the markings on the axes and puts labels on the x- and y-axes but units are not given for water level on the y-axis. The candidate shows the work for how the rate of water loss is computed but provides no discussion to explain why these numbers were chosen or the possible flaws in this choice. The candidate also gives a range of heights of water but does not explain why these numbers were chosen. The influences are simply listed without any explanation of how they would affect the prediction. Rationale: The response reflects a limited, poorly reasoned understanding of the problem. The arithmetic for the rate of loss is partially correct (should be 4 weeks not 5, week 5 minus week 1 equals 4 = 4), but the candidate never recognizes that the rate of loss is increasing, and therefore the calculated rate is too low. The candidate does not clearly state or demonstrate their reasoning for the choices used to make predictions. Statements are made without explanation that would demonstrate understanding. |
||||||||||
| Second Sample Weak Response |
Second Sample Weak Response to Open-Response Item Assignment #2 1. See graph. 2. From 109 to 92, the first four weeks, no supplemental water was added, so 109 minus 92 equals 17 and 17 divided by 4 is about 4. The rate of water is 4 inches a week. At ten weeks we have 68 inches in the reservoir so 68 divided by 4 equals about 17 weeks. This means that we have more than enough water to get to October without adding anything. We only need ten more weeks of water. 3. No more water is needed. In the last ten weeks from July 27 to the beginning of October there will still be 28 inches of water in the reservoir but that doesn’t seem like it would be enough. Let’s always assume that at least 5 feet of water is in the reservoir which is 60 inches. 60 minus 28 equals 32 inches of water needed to get back up to 60 inches I know that the supplemental adds 4 inches a week. 32 divided by 4 equals 8 so 8 weeks of additional water will be needed. 20 minus 8 equals 12 weeks so at the latest water should be added starting at 12 weeks. 4. Influencing my predictions: How I chose my intervals will affect my rate. Which week I start between week 1 and week 10 will affect my decision on how long the water will last. A graph displays data from the stimulus plotted as a disconnected set of points. The points are plotted incorrectly: The y-values of the points match those from the data table in the stimulus. The x-values of the points read as follows:1, 2, 3, 3.5, 4.5, 4.4, 6.5, 8, 9, 10. The vertical axis has a range from 60 to 110. Every 3 units represents a change of 10, and every third unit is labeled. The interval on this axis between 0 and 60 is shown as a squiggly line. The horizontal axis has a range from 1 to 10 and every unit represents 1 week. Only the fifth and tenth weeks are labeled. The y axis is labeled water and the x axis is labeled weeks. |
||||||||||
| Second Weak Response Analysis |
Analysis of Second Weak Response to Open-Response Item Assignment #2 Purpose: The purpose of the assignment is partially achieved. All parts of the prompt were attempted. The graph is labeled minimally, and points plotted relatively accurately. Work was given for the second part, finding the rate, and partially correctly done (should be 3 weeks not 4 [week 1 minus 4 equals 3 ]), but the candidate gives no explanation of why this range was chosen. The third part was answered and explained well but the assumptions made were incorrect. The last part has some possible influences that would affect the predictions but no reasoning for why these would affect the result. Subject Matter Knowledge: The response shows knowledge of how to plot a graph though it could be more carefully plotted and axes labeled with units. The use of the first four weeks to find the rate before any supplemental water was added was a good interval to use, and finding the rate was a correct procedure, but rounding the answer added to possible inaccuracy, and it should be noted that the week span is only 3 weeks, not 4. The response did not recognize that the rate of loss was increasing by week 5, making the average computed too low. In the third part of the prompt, the response was not reasoned correctly. There was never recognition that water was supplemented starting at week five. The use of the 68, which included five weeks of supplemental water, was used to find the answer and this was never recognized, leading to an incorrect estimate. A logical reason was given for wanting a minimum of 5 feet but again not recognizing that water had already been supplemented led to another incorrect conclusion. Lastly, the influences given could be reasonable but needed to defend why these would affect the prediction. Support: Since there was a table given, none needed to be included with their graph. Break in the y-axis was shown which shows an understanding of the whole axis not being shown. Labels should have included more information, for example, adding the words “the level of water in inches" on the y-axis would communicate more information. Support was good for finding the rate used, but no explanation was given as to why that interval was a good choice. No analysis of how the rate of loss was increasing by week 5 to a change of 8 inches was included and how that would make the rate chosen too low. No explanation was given for the choice of using 68 inches at week 10 as the starting point for answering the question presented but does state a conclusion based on their reasoning. Part three is supported well, giving reasons why each step is used; however, assumptions made earlier are flawed. The influences stated are possible, but support is needed to explain why these would affect the prediction and why they were chosen. Rationale: The overall impression of this response is that it is limited and partially correct, with poor reasoning in several parts, but there are parts that are supported and reasoned appropriately. The claim that the height of the water decreases by a rate of 4 inches per week in the first four weeks is too low. The data show the height decreases by more than 4 inches per week during this interval. In the third part, work was clearly shown and reasons given for the steps used even though the assumptions were incorrect. Though two influences were found, it would improve the response by also giving a situational influence (for example, supplemental water was an estimate and mechanical failures would affect the rate), and all influences needed explanation as to why they could affect the prediction given. |
||||||||||
| First Sample Strong Response |
First Sample Strong Response to Open-Response Item Assignment #2 The rate of water loss is going to be based on the data from the 10-week period from May through July. I am going to use the first 4 weeks of data before they started adding 4 inches of water to get the rate of water usage. Using figures from the table, subtract 92 (level at week 4) from 109 (level at week 1), which results in 17 inches lost. Dividing 17 by 3 weeks will give us the rate of 5.67 inches per week. At Week 10, the water level was 68, but that reflected at least 5 weeks of additional 4 inches per week of water added. On week 5 the process of adding an additional four inches was started but it would take time to have an effect, so decided not to include it in the computation. Without this addition, it would be 48 inches of water instead of 68 inches. ( 5 weeks times 4 inches of water added = 20 inches of additional water. 68 minus 20 equals 48 inches.) To predict when the reservoir would have run out of water (reached 0) if the additional reserves were not added, we would have to lose an additional 48 inches of water. 48 divided by 5.67 (the average loss) would be about 9 more weeks but it is only ten more weeks until Oct. 1 so in theory additional water would be needed. 0 is less than w is less than 68 minus 5.67t where 0 is less than t is less than 10 . The remaining ten weeks is defined by t. The range for w was chosen because there are 68 inches of water at the end of 10 weeks for the upper limit. The lower limit should never reach zero water in the reservoir. The remaining 10 weeks until Oct. 1 are defined by t. Reasons the calculations would be inaccurate: If usage goes up in the last ten weeks, it affects our calculation and more water would have to be added. If there was an unexpected large amount of rain which is atypical, then water levels would be high and additional water would not be needed. Also, I based my prediction on the average loss during the 4 weeks in the table. If I were to base my prediction on the first 5 weeks only, my rate would be different, which would affect the prediction of when the reservoir runs dry. A graph correctly displays data from the stimulus. Straight line segments connect each point, and each point is labeled with its coordinates. The y axis is labeled height of water in inches and the x axis is labeled week. The vertical axis has a range from 68 to 110. The first label begins 3 units from the origin. Every 1 vertical unit represents a change of 2 inches, and every unit is labeled. A squiggly line is drawn over the vertical axis between the origin and y equals 68. The corresponding label for this interval shows 3 dots. The horizontal axis has a range from 1 to 10, and every 2 units represents a change of 1 week. All 10 weeks are labeled. |
||||||||||
| First Strong Response Analysis |
Analysis of First Strong Response to Open-Response Item Assignment #2 Purpose: The candidate has responded fully to all the parts of the prompt. A graph was drawn for the first question. An equation was found to predict what week there would be no more water. A range for the water level was found and explained. Things that could affect the prediction were stated and explained how they would affect the prediction. Subject Matter Knowledge: There is substantial, accurate and appropriate application of subject matter knowledge. The chart of values is plotted on the x-y graph to see the shape of the curve. The graph is carefully drawn and labeled clearly, and the scale is shown. Analysis is provided to explain how the rate of water loss was found. Assumptions that were made are explained. A range of values is computed to see when water needed to be added. Possible outside forces that might affect the predictions and what effect it would have on water levels are discussed. Support: Supporting evidence is found for each part. The graph is drawn with clearly defined and labeled axes, and each point on the graph has its coordinate given. Calculations for how the rate of water loss were found and the reasoning for the choices are provided. An equation for the limits on the loss of water before actions needed to be taken is developed and explained. Some possible reasons why the prediction might not be accurate are given and explained. Rationale: The response reflects an ably reasoned understanding of the topic. The graph reflects the relationship between different weeks and water height. The data used to find the rate of water loss is clearly shown, and reasons for using that data are explained. Each part of the prompt explains the reasoning used and shows calculations so that the process can be clearly understood. |
||||||||||
| Second Sample Strong Response |
Second Sample Strong Response to Open-Response Item Assignment #2 1: See graph. 2: I am assuming that week 5 has not had water added – so they added water (4 inches per week) in weeks 6 to 10. At week 10 there would be 20 inches of water less if there was no supplement (5 weeks times 4 inches of water added = 20 inches of water) 68 minus 20 = 48 inches at week 10 instead of 68 inches . To find the rate of loss over the ten weeks when no supplemental water was added I will find the difference between week 1 (109 inches ) and the 48 inches calculated at week 10 when no extra water was added to the reservoir. The water changed by 109 minus 48 = 61 inches from week 1 to week 10 and at an average rate of 61 divided by 9 = 6.8 inches per week. Assume that the reservoir can/will go down to zero then 48 minus 6.8t = 0 if t = number of weeks until it is empty 48 = 6.8t and t = 7.1 weeks. The reservoir will be empty at this rate between 7 and 8 weeks after the first ten weeks, between the 17th and 18th week. Additional water will be needed since it will be 3 more weeks before Oct. 1. 3: Assume ten more weeks until the beginning of t = the number of weeks until Oct. 1 after week 10 and w = the depth of the water at the end of each week in inches I found the average rate of loss from week 5 through 10 when water was added each week. 84 inches minus 68 inches equals 16 inches and 16 inches divided by 5 inches of loss each of the last five weeks in the table. 68 minus 3.2t equals 0 0 is less than t is less than 10 weeks 68 is greater than w is greater than 36 inches At the end of 10 weeks 68 minus 3.2 times 10 equals 36 inches of water left in the reservoir. 4: Factors that would influence my predictions/accuracy would include:
a. My assumptions could be false. For example, letting the water go to 0 would not be logical, safe, or reasonable. A graph correctly displays data from the stimulus. The points are not connected. The y axis is labeled level of h 2 o in reservoir open paren inches close paren. The vertical axis has a range from 0 to 110. Every 2 vertical units represents a change of 10 inches, and every other unit is labeled. The horizontal axis is labeled week number, open paren t close paren. Every 2 horizontal units represents 1 week. Week 1 to 3 and 7 to 10 are labeled. The axis label occupies the position of where weeks 4, 5, and 6 would be labeled. |
||||||||||
| Second Strong Response Analysis |
Analysis of Second Strong Response to Open-Response Item Assignment #2 Purpose: The purpose of the assignment was fully achieved. Each part is thoroughly completed with calculations shown and explanation of the reasoning used. All assumptions are stated and reasoning explained. Subject Matter Knowledge: Part 1 shows a carefully labeled and plotted graph of the given table of water depth over a ten-week period. Part 2 provides an explanation of the assumptions that were used and resulting calculations. The result yields a well-reasoned prediction that water would need to be added before Oct. 1. Part 3 includes an equation and ranges for both t and w that are reasonable, calculated, and justified fully. Part 4 shows an understanding of the physical situation and lists many possible scenarios that would affect the prediction. Support: The supporting evidence is sound. Part 1 demonstrates a clear, easy-to-read and understand graph of the situation. Part 2 states assumptions and includes the reasons why those assumptions were made. The work to arrive at a conclusion is clearly shown and explained. Part 3 re-evaluates the situation with the information that there will not be enough water and re-assesses the parameters that were used, giving a reasonable new predication for the situation. Part 4 lists five plausible scenarios that could change the prediction, showing an understanding of the real-world situation given. Rationale: The response reflects an ably reasoned, comprehensive understanding of the topic. All parts are addressed and thoroughly reasoned with clear explanations given for assumptions used, calculations made, and conclusions formulated. |
||||||||||
| Review the Performance Characteristics and Score Scale for Written Performance Assignments. | |||||||||||
Multiple Choice Question
Practice Test Evaluation Chart
In the evaluation chart that follows, the multiple-choice questions are arranged in numerical order and by test objective. Check your responses against the correct responses provided to determine how many questions within each objective you answered correctly.
Subarea 1 : Number Sense and Operations
Objective 0001: Apply knowledge of the properties and structure of the real number system.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 1 | B | |
| 2 | B | |
| 3 | A | |
| 4 | C | |
| 5 | C |
out of 5
Objective 0002: Apply knowledge of the properties and structure of the complex number system and linear algebra.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 6 | B | |
| 7 | B | |
| 8 | B | |
| 9 | A | |
| 10 | A |
out of 5
Subarea 1 (Objectives 0001–0002) Total out of 10
Subarea 2 : Relations, Functions, and Algebra
Objective 0003: Analyze and apply algebraic techniques to expressions, equations, and inequalities.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 11 | B | |
| 12 | A | |
| 13 | B | |
| 14 | A | |
| 15 | D | |
| 16 | A |
out of 6
Objective 0004: Apply the principles and properties of relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 17 | C | |
| 18 | C | |
| 19 | C | |
| 20 | B | |
| 21 | C |
out of 5
Objective 0005: Apply the principles and properties of linear, absolute value, and quadratic relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 22 | B | |
| 23 | B | |
| 24 | B | |
| 25 | C | |
| 26 | A |
out of 5
Objective 0006: Apply the principles and properties of exponential and logarithmic relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 27 | A | |
| 28 | B | |
| 29 | A | |
| 30 | A | |
| 31 | C | |
| 32 | B |
out of 6
Objective 0007: Apply the principles and properties of polynomial, radical, and rational relations and functions.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 33 | B | |
| 34 | D | |
| 35 | D | |
| 36 | C | |
| 37 | B | |
| 38 | C |
out of 6
Objective 0008: Apply the principles and properties of trigonometric functions and identities.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 39 | A | |
| 40 | A | |
| 41 | B | |
| 42 | C | |
| 43 | B |
out of 5
Subarea 2 (Objectives 0003–0008) Total out of 33
Subarea 3 : Geometry and Measurement
Objective 0009: Apply the principles, concepts, and procedures related to units and measurement.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 44 | C | |
| 45 | C | |
| 46 | B | |
| 47 | D |
out of 4
Objective 0010: Apply the axiomatic structure of Euclidean geometry.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 48 | C | |
| 49 | B | |
| 50 | A | |
| 51 | A | |
| 52 | B |
out of 5
Objective 0011: Apply the principles and properties of Euclidean geometry to solve problems involving two- and three-dimensional objects.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 53 | B | |
| 54 | C | |
| 55 | D | |
| 56 | A | |
| 57 | D |
out of 5
Objective 0012: Apply the principles and properties of coordinate and transformational geometry and the characteristics of non-Euclidean geometries.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 58 | D | |
| 59 | C | |
| 60 | A | |
| 61 | C | |
| 62 | B | |
| 63 | D |
out of 6
Subarea 3 (Objectives 0009–0012) Total out of 20
Subarea 4 : Probability, Statistics, Calculus, and Discrete Mathematics
Objective 0013: Apply the principles, properties, and techniques of probability.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 64 | C | |
| 65 | B | |
| 66 | C | |
| 67 | A |
out of 4
Objective 0014: Apply the principles and concepts of descriptive statistics to the problem-solving process.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 68 | D | |
| 69 | B | |
| 70 | B | |
| 71 | A |
out of 4
Objective 0015: Apply principles and techniques of limits, continuity, and differential calculus.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 72 | A | |
| 73 | A | |
| 74 | B | |
| 75 | C | |
| 76 | A |
out of 5
Objective 0016: Apply principles and techniques of integral calculus.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 77 | D | |
| 78 | C | |
| 79 | B | |
| 80 | A | |
| 81 | B |
out of 5
Objective 0017: Apply the properties and techniques of discrete mathematics.
| Question Number | Your Response | Correct Response |
|---|---|---|
| 82 | D | |
| 83 | C | |
| 84 | C | |
| 85 | B |
out of 4
Subarea 4 (Objectives 0013–0017) Total out of 22
Practice Test Score Calculation
The practice test score calculation is provided so that you may better gauge your performance and degree of readiness to take an MTEL test at an operational administration. Although the results of this practice test may be used as one indicator of potential strengths and weaknesses in your knowledge of the content on the official test, it is not possible to predict precisely how you might score on an official MTEL test.
The Sample Responses and Analyses for the open-response items may help you determine whether your responses are more similar to the strong or weak samples. The Scoring Rubric can also assist in estimating a score for your open responses. You may also wish to ask a mentor or teacher to help evaluate your responses to the open-response questions prior to calculating your total estimated score.
How to Calculate Your Practice Test Score
Review the directions in the sample below and then use the blank practice test score calculation worksheet to calculate your estimated score.
Multiple-Choice Section
| Enter the total number of multiple-choice questions you answered correctly: | 53 | ||
| Use Table 1 below to convert that number to the score and write your score in Box A: | A: | 192 |
Open-Response Section
| Enter the number of points (1 to 4) for your first open-response question: | 3 | ||
| Enter the number of points (1 to 4) for your second open-response question: | 3 | ||
| Add those two numbers (Number of open-response question points): | 6 | ||
| Use Table 2 below to convert that number to the score and write your score in Box B: | B: | 52 |
Total Practice Test Score (Estimated MTEL Score)
| Add the numbers in Boxes A and B for an estimate of your MTEL score: | A + B = | 244 |
Practice Test Score Calculation Worksheet: Mathematics (63)
Table 1:
| Number of Multiple-Choice Questions Correct | Estimated MTEL Score |
|---|---|
| 0 to 25 | 147 |
| 26 to 30 | 155 |
| 31 to 35 | 162 |
| 36 to 40 | 170 |
| 41 to 45 | 177 |
| 46 to 50 | 185 |
| 51 to 55 | 192 |
| 56 to 60 | 200 |
| 61 to 65 | 207 |
| 66 to 70 | 215 |
| 71 to 75 | 222 |
| 76 to 80 | 230 |
| 81 to 85 | 237 |
| 86 to 90 | 245 |
| 91 to 95 | 252 |
| 96 to 100 | 260 |
Table 2:
| Number of Open-Response Question Points | Estimated MTEL Score |
|---|---|
| 2 | 36 |
| 3 | 40 |
| 4 | 44 |
| 5 | 48 |
| 6 | 52 |
| 7 | 56 |
| 8 | 60 |
Use the form below to calculate your estimated practice test score.
Multiple-Choice Section
| Enter the total number of multiple-choice questions you answered correctly: | |||
| Use Table 1 above to convert that number to the score and write your score in Box A: | A: |
Open-Response Section
| Enter the number of points (1 to 4) for your first open-response question: | |||
| Enter the number of points (1 to 4) for your second open-response question: | |||
| Add those two numbers (Number of open-response question points): | |||
| Use Table 2 above to convert that number to the score and write your score in Box B: | B: |
Total Practice Test Score (Estimated MTEL Score)
| Add the numbers in Boxes A and B for an estimate of your MTEL score: | A + B = |
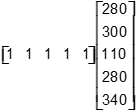 = [280 + 300 + 110 + 280 + 340] = [1310]
= [280 + 300 + 110 + 280 + 340] = [1310]
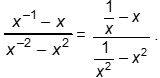
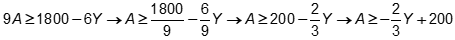
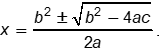
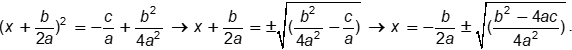
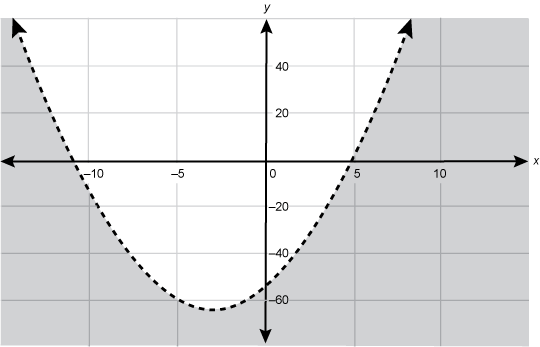
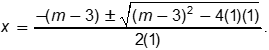
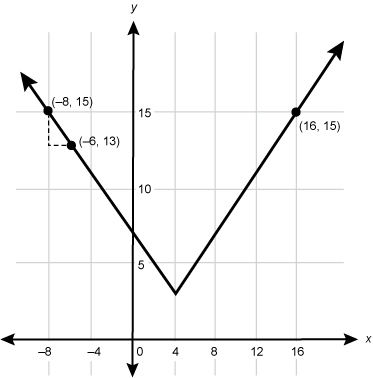
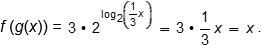
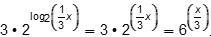
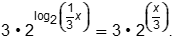
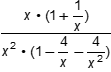
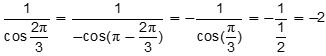 .
.
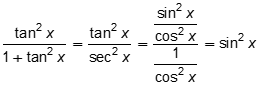
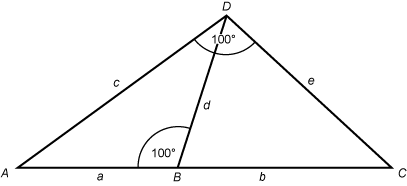
 •
h =
•
h = 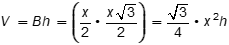
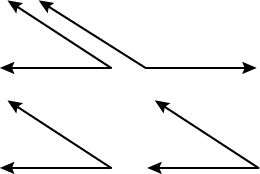
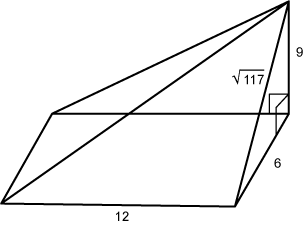
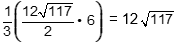
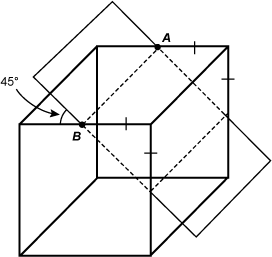

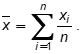

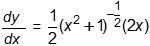 .
.
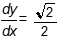
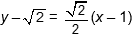
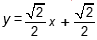 .
.
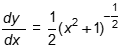
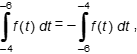
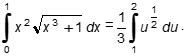
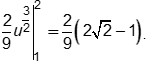
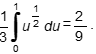
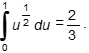
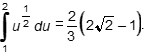
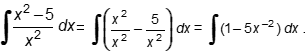
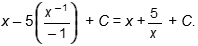
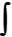 (1 − 5x−2)dx,
(1 − 5x−2)dx,
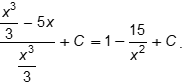 .
.
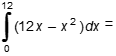
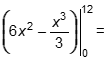 6 • 144 − 576 = 288.
6 • 144 − 576 = 288.
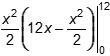 = 72 • 72 = 5184.
= 72 • 72 = 5184.
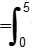 1.2e0.14tdt.
1.2e0.14tdt.
 = 8.57(e0.14 • 5 − e0)
≈ 8.7
= 8.57(e0.14 • 5 − e0)
≈ 8.7