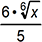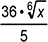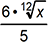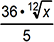Test Information Guide

Field 63: Mathematics
Sample Multiple-Choice Questions

Expand All | Collapse All

The following reference material will be available to you during the test:

Formulas

Candidates taking the Mathematics test (field 63) will be provided with an on-screen scientific calculator with functions that include the following: addition, subtraction, multiplication, division, square root, percent, sine, cosine, tangent, exponents, and logarithms. You may NOT bring your own calculator to the test.

Number Sense and Operations

Objective 0001
Apply knowledge of the properties and structure of the real number system.

1. A student claims that performing an operation of the type ^a/_b − ^c/_dthe value a over the value b minus the value c over the value d requires determining the smallest integer that is divisible by b and d. For the student's claim to be true, which of the following statements must also be true?

1. a, b, c, and d are positive integers.
2. b and d are relatively prime.
3. a and c are relatively prime.
4. b and d are both integers.

Answer

Correct Response: D.

Correct Response: D.

---

Objective 0001
Apply knowledge of the properties and structure of the real number system.

2. If x is a positive real number, which of the following expressions is equivalent to ?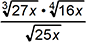

1. 
2. 
3. 
4. 

Answer

Correct Response: C.

Correct Response: C.

---

Objective 0002
Apply knowledge of the properties and structure of the complex number system and linear algebra.

3. Use the information below to answer the question that follows.

According to de Moivre's theorem, what is the value of z⁶ if z = −1 + i z to the sixth power if z equals negative 1 plus i ?

1. −8 negative 8 
2. −8i negative 8 i  
3. 8
4. 8i 8 i  

Answer

Correct Response: D.

Correct Response: D.

---

Relations, Functions, and Algebra

Objective 0004
Apply the principles and properties of relations and functions.

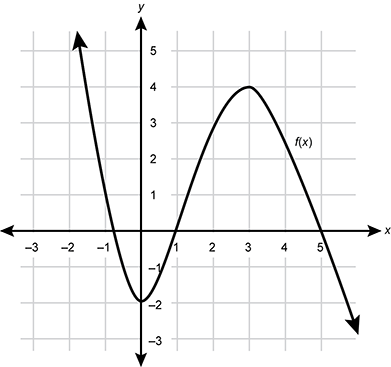
4. Use the graph below to answer the question that follows.

A graph showing a function labeled f of x on the x y coordinate plane. Starting on the left the function emerges from the top of the graphing area and decreases sharply, passing through the point negative 1 comma 1, and reaching a minimum at the point 0 comma negative 2. It then increases sharply, crosses the x axis at the point 1 comma 0, and reaches a maximum at the point 3 comma 4. After this it begins to decrease again, crosses the x axis at the point 5 comma 0, and leaves the graph at the bottom right corner.

Given the graph of f(x)f of x shown, what is the value of ^{2f(–1) − f(3)}/_f(0) 2 times the function of negative 1 minus the function of 3 all over the function of 0?

1. undefined
2. 0
3. 1
4. 3

Answer

Correct Response: C.

Correct Response: C.

---

Objective 0004
Apply the principles and properties of relations and functions.

5. The set {a_n} represents an arithmetic sequence. If a₈ = ⁴¹/₂ and a₁₆ = ⁸¹/₂, which of the following recursive formulas represents {a_n}?  The set A sub n represents an arithmetic sequence. If the eighth term is 41 halves and the sixteenth term is 81 halves, which of the following recursive formulas represents a sub n? 

1. a₁ = 0
   a_n = ⁵/₂ a_n−1 + ¹/₂  A sub 1 equals 0, A sub n equals 5 halves times the previous term plus one half 
2. a₁ = ¹/₂
   a_n = a_n−1 + ⁵/₂  A sub 1 equals one half, A sub n equals the previous term plus 5 halves 
3. a₁ = 0
   a_n = ⁵/₂ a_n−1 + 3  A sub 1 equals 0, A sub n equals 5 halves times the previous term plus 3 
4. a₁ = 3
   a_n = a_n−1 + ⁵/₂  A sub 1 equals 3, A sub n equals the previous term plus 5 halves 

Answer

Correct Response: D.

Correct Response: D.

---

Objective 0005
Apply the principles and properties of linear, absolute value, and quadratic relations and functions.

6. Over the course of a summer, a child sets up a lemonade stand beside a busy bicycle path. When the child charges $0.25 per cup, 75 cyclists purchase lemonade each day, and when the child charges $0.50 per cup, 60 cyclists purchase lemonade each day. Assuming that lemonade sales can be modeled by a linear function, how much money should the child expect to collect at the end of a day on which the price of lemonade is $0.70 per cup?

1. $33.60
2. $39.00
3. $42.00
4. $50.40

Answer

Correct Response: A.

Correct Response: A.

---

Objective 0005
Apply the principles and properties of linear, absolute value, and quadratic relations and functions.

7. It costs a company $10,62010 thousand 6 hundred twenty dollars to manufacture 20 units of a certain air conditioner. It costs the company $14,940 to manufacture 30 units. Assuming that the data fit a linear function, how much will it cost the company to manufacture 36 units?

1. $15,55215 thousand five hundred fifty two dollars
2. $17,53217,532 dollars
3. $18,12618,126 dollars
4. $18,52218,522 dollars

Answer

Correct Response: B.

Correct Response: B.

---

Objective 0006
Apply the principles and properties of exponential and logarithmic relations and functions.

8. Use the table below to answer the question that follows.

x	y
0.1	1.5
10 square root of 10	0
1000	– negative 2.5

An equation written in the form y = m • log(x) times log of x + n could represent the relation shown in the table, where m and n are constants. What is the value of n?

1. 2.5
2. 0.5
3. – negative 0.5
4. – negative 5.5

Answer

Correct Response: B.

Correct Response: B.

---

Objective 0006
Apply the principles and properties of exponential and logarithmic relations and functions.

9. A person invests $10,00010 thousand dollars at a 5% annual interest rate compounded quarterly. Solving which of the following equations yields t, the doubling time in years?

1. e^0.0125t = 2  e to the power of 0.0125 t equals 2 
2. e^0.05t = 2  e to the power of 0.05 t equals 2 
3. (1.0125)^4t = 2  1.0125 to the power of 4 t equals 2 
4. (1.05)^4t = 2  1.05 to the power of 4 t equals 2 

Answer

Correct Response: C.

Correct Response: C.

---

Objective 0007
Apply the principles and properties of polynomial, radical, and rational relations and functions.

10. Let f(x) = x³ − a²x  f of x equal x cubed minus a squared x , where a is a positive real number. Which of the following is a true statement about the graph of f(x) f of x ?

1. y = −x is a line of symmetry of f(x) y = negative x is a line of symmetry of f of x .
2. f(x) f of x  has exactly two real roots.
3. y = x − a is a slant asymptote of f(x) y = x minus a is a slant asymptote of f of x .
4. f(x) f of x  has exactly two critical points.

Answer

Correct Response: D.

Correct Response: D.

---

Objective 0008
Apply the principles and properties of trigonometric functions and identities.

11. Which of the following expressions is equivalent to ¹/_{csc θ − sin θ}1 over cosecant theta minus sine theta?

1. tan²θtangent squared theta
2. tan θ • sec θtangent theta times secant theta
3. cot²θcotangent squared theta
4. cot θ • cos θcotangent theta times cosine theta

Answer

Correct Response: B.

Correct Response: B.

---

Objective 0008
Apply the principles and properties of trigonometric functions and identities.

12. Use the equation below to answer the question that follows.

sin²(2x) = cos²(2x) sine squared 2 x = cosine squared 2 x 

What is the difference between the two smallest positive solutions of the equation shown?

1. ^π/₆one sixth pi
2. ^π/₄one fourth pi
3. ^π/₃one third pi
4. ^π/₂one half pi

Answer

Correct Response: B.

Correct Response: B.

---

Geometry and Measurement

Objective 0009
Apply the principles, concepts, and procedures related to units and measurement.

13. Two right triangular prisms are similar. Each edge of the smaller prism measures one-third of the length of the corresponding edge in the larger prism. If the total surface area of the larger prism is 216 square inches, what is the total surface area of the smaller prism?

1. 24 square inches
2. 36 square inches
3. 60 square inches
4. 72 square inches

Answer

Correct Response: A.

Correct Response: A.

---

Objective 0009
Apply the principles, concepts, and procedures related to units and measurement.

14. A sign has the shape of a regular octagon with side lengths measuring 1 foot. Which of the following expressions represents the area of the sign in square feet?

1. 2 √ 2 radical 2 + 1
2. 4 √ 2 radical 2 + 2
3. 2 √ 2 radical 2 + 2
4. 4 √ 2 radical 2 + 4

Answer

Correct Response: C.

Correct Response: C.

---

Objective 0010
Apply the axiomatic structure of Euclidean geometry.

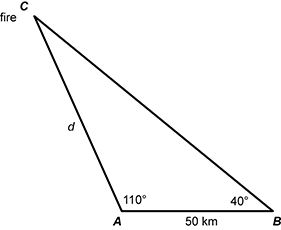
15. Use the diagram below to answer the question that follows.

A diagram showing a triangle A B C. Point C is the location of the fire. The distance between point A and point B is 50 kilometers. The distance between point A and point C is labeled d. Angle A measures 110 degrees, and angle B measures 40 degrees.

Two watchtowers located at points A and B have visual contact with a fire located at point C. The watchtowers are 50 kilometers apart and have views of the fire at the angles shown in the diagram. Which of the following equations can be solved to determine d, the distance between the fire and the watchtower located at point A?

1. d sin 30° = 50 sin 110°d sine 30 degrees = 50 sine 110 degrees
2. 50 sin 40° = d sin 30°50 sine 40 degrees = d sine 30 degrees
3. d sin 110° = 50 sin 40°d sine 110 degrees = 50 sine 40 degrees
4. 50 sin 30° = d sin 110°50 sine 30 degrees = d sine 110 degrees

Answer

Correct Response: B.

Correct Response: B.

---

Objective 0010
Apply the axiomatic structure of Euclidean geometry.

16. Students are creating logos that will contain triangles in which they want to inscribe circles. To find the centers of these circles, the students should construct the three:

1. altitudes of each triangle.
2. medians of each triangle.
3. angle bisectors of each triangle.
4. perpendicular bisectors of the sides of each triangle.

Answer

Correct Response: C.

Correct Response: C.

---

Objective 0011
Apply the principles and properties of Euclidean geometry to solve problems involving two- and three-dimensional objects.

17. Which of the following statements is true in three-dimensional Euclidean space?

1. If a line is perpendicular to a plane, then it is perpendicular to any line in the plane.
2. If two lines are each perpendicular to a third line, then they are parallel to each other.
3. If a line is perpendicular to each of two planes, then the planes are parallel.
4. If two planes are each perpendicular to the same plane, then they are parallel to each other.

Answer

Correct Response: C.

Correct Response: C.

---

Objective 0012
Apply the principles and properties of coordinate and transformational geometry and the characteristics of non-Euclidean geometries.

18. If the graph of ^y2/₉ − ^x2/₁₆the value y squared over 9 minus the value x squared over 16 equals 1 undergoes a 90° degrees clockwise rotation about the origin, which of the following points is a focus of the transformed graph?

1. (– negative 5, 0)
2. (– negative 3, 0)
3. (0, 4)
4. (0, 5)

Answer

Correct Response: A.

Correct Response: A.

---

Objective 0012
Apply the principles and properties of coordinate and transformational geometry and the characteristics of non-Euclidean geometries.

19. Use the graph below to answer the question that follows.

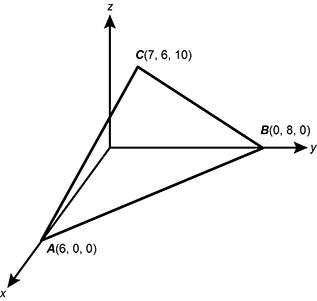
A triangle is graphed in a three-dimensional coordinate system. Vertex A is located at 6, 0, 0, vertex B is located at 0, 8, 0, and vertex C is located at 7, 6, 10.

The vertices of a triangle ABC A B C  in a three-dimensional coordinate system are A(6, 0, 0), B(0, 8, 0), and C(7, 6, 10). What is the length of the median from point C to side AB A B ?

1. 10
2. 2 √ 30  radical 30  
3. 16
4. 10 √ 3  radical 3  

Answer

Correct Response: B.

Correct Response: B.

---

Probability, Statistics, Calculus, and Discrete Mathematics

Objective 0013
Apply the principles, properties, and techniques of probability.

20. The owners of an orange grove project a profit for the next growing season of $240,000. However, it is predicted that there is a 12% chance that the grove will experience a damaging insect infestation. In that case, the projected profit is $60,000. Profit-protection insurance of $240,000 is available for $30,000. In order to decide whether to buy the insurance, the owners calculate the expected profit with and without insurance. Without insurance, the expected profit is $218,400. What is the expected profit if the owners do buy insurance?

1. $217,200
2. $236,400
3. $243,600
4. $270,000

Answer

Correct Response: A.

Correct Response: A.

---

Objective 0013
Apply the principles, properties, and techniques of probability.

21. A band's 20 most popular songs from their previous albums were released on a new greatest hits album. Two songs from the first album appear on the greatest hits album. The songs are played in a random order that allows for repetition. If the probability that the first song played comes from the first album and the second song played comes from the second album is 3%, what fraction of the songs on the greatest hits album come from the band's first two albums?

1. ³/₁₀ 3 tenths
2. ²/₅ 2 fifths
3. ¹/₂ 1 half
4. ⁴/₅ 4 fifths

Answer

Correct Response: B.

Correct Response: B.

---

Objective 0014
Apply the principles and concepts of descriptive statistics to the problem-solving process.

22. According to which of the following horizontal bar charts was the median number of cars sold per day equal to the mean number of cars sold per day?

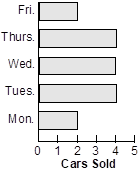1. A horizontal bar graph shows the number of cars sold on different days of the week. There were 2 cars sold on Monday, 4 cars sold on Tuesday, Wednesday, and Thursday and 2 cars sold on Friday.


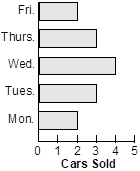2. A horizontal bar graph shows the number of cars sold on different days of the week. There were 2 cars sold on Monday, 3 cars sold on Tuesday, 4 cars sold on Wednesday, 3 cars sold on Thursday and 2 cars sold on Friday.


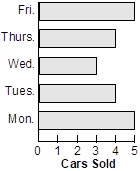3. A horizontal bar graph shows the number of cars sold on different days of the week. There were 5 cars sold on Monday, 4 cars sold on Tuesday, 3 cars sold on Wednesday, 4 cars sold on Thursday and 5 cars sold on Friday.


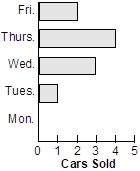4. A horizontal bar graph shows the number of cars sold on different days of the week. There were 0 cars sold on Monday, 1 car sold on Tuesday, 3 cars sold on Wednesday, 4 cars sold on Thursday and 2 cars sold on Friday.

Answer

Correct Response: D.

Correct Response: D.

---

Objective 0015
Apply principles and techniques of limits, continuity, and differential calculus.

23. Which of the following statements about the function y = ^6x/_{x² + 1}6 x over the quantity x squared plus 1 is true?

1. No maximum or minimum value of the function exists.
2. The maximum value of the function is 3.
3. The maximum value of the function occurs at x = 1 and x = – negative 1.
4. The minimum value of the function is 0.

Answer

Correct Response: B.

Correct Response: B.

---

Objective 0015
Apply principles and techniques of limits, continuity, and differential calculus.

24. At what value(s) of x, if any, do points of inflection occur on the graph of ?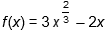

1. x = − negative 1
2. x = 0
3. x = 1
4. There are no points of inflection.

Answer

Correct Response: D.

Correct Response: D.

---

Objective 0017
Apply the properties and techniques of discrete mathematics.

25. A television station shows an "adopt a pet" program featuring dogs and cats from a local shelter once each month. Three dogs and three cats will be chosen for today's program. If the shelter has 6 dogs and 8 cats, all equally likely to be chosen, how many different sets of animals could be chosen for the program?

1. 1,120
2. 4,480
3. 10,080
4. 40,320

Answer

Correct Response: A.

Correct Response: A.

---

Copyright © 2020 Pearson Education, Inc. or its affiliate(s). All rights reserved.
Pearson, 300 Venture Way, Hadley, MA 01035